CTF-web Xman-2018 crypto 古典密码和简单入门rsa题目
Rotator
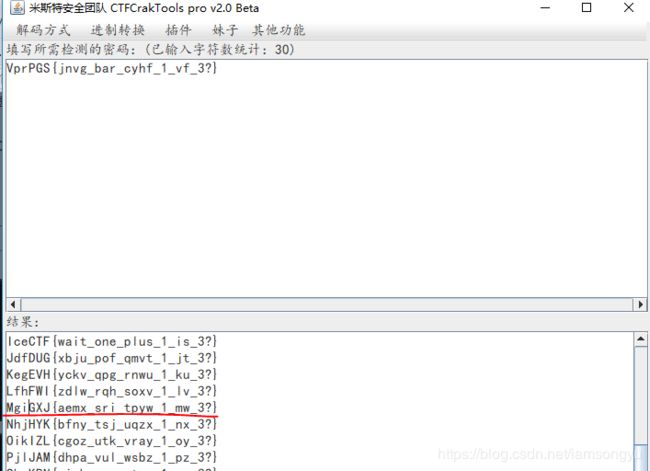
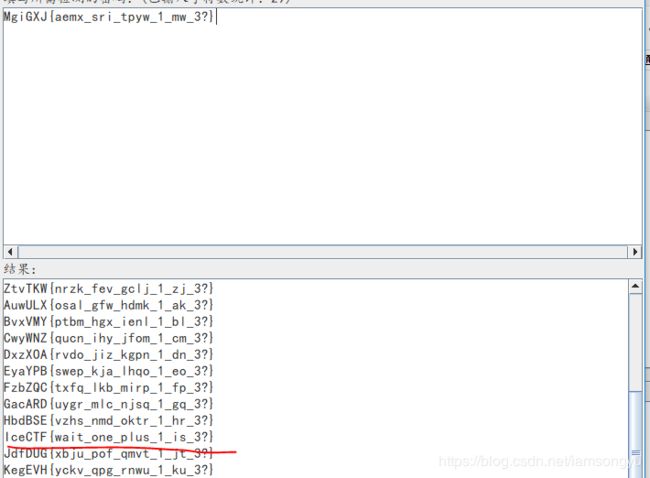
这是一道凯撒密码的题目,题目里提示先五移位,在八移位就可以得到
完成,这里使用的软件米斯特安全工具或者使用在线的工具也可以
单表替换密码
Lw!
Gyzvecy ke WvyVKT!
W'zz by reso dsbdkwksky tzjq teo kly ujr. Teo keujr, gy joy dksurwmq bjdwv vorakeqojalr jmu wkd jaazwvjkwemd. Vorakeqojalr ljd j zemq lwdkeor, jzklesql gwkl kly juxymk et vecaskyod wk ljd qekkym oyjzzr vecazwvjkyu. Decy dwcazy ezu vwalyod joy kly Vjydjo vwalyo, kly Xwqymyoy vwalyo, kly dsbdkwkskwem vwalyo, glwvl wd klwd emy, jmu de em. Jzcedk jzz et klydy vwalyod joy yjdwzr boeiym keujr gwkl kly lyza et vecaskyod. Decy myg ymvorakwem cykleud joy JYD, kly vsooymk dkjmujou teo ymvorakwem, jzemq gwkl ODJ. Vorakeqojalr wd j xjdk twyzu jmu wd xyor wmkyoydkwmq klesql. De iwvi bjvi, oyju sa em decy veez vwalyod jmu ljxy tsm!
El jmu teo reso oyveoud cr mjcy wd WvyVKT{jzgjrd_zwdkym_ke_reso_dsbdkwksky_tzjqd}.大多数时候可以使用在线网站进行词频分析,如https://quipqiup.com/,这种特别原理的题目的则是没什么太大的技术
提交已知信息,加大成功率
Hi! Welcome to IceCTF! I'll be your substitute flag for the day. For today, we are studying basic cryptography and its applications. Cryptography has a long history, although with the ad?ent of computers it has gotten really complicated. Some simple old ciphers are the Caesar cipher, the ?igenere cipher, the substitution cipher, which is this one, and so on. Almost all of these ciphers are easily bro?en today with the help of computers. Some new encryption methods are AES, the current standard for encryption, along with RSA. Cryptography is a ?ast field and is ?ery interesting though. So ?ic? bac?, read up on some cool ciphers and ha?e fun! Oh and for your records my name is IceCTF{always_listen_to_your_substitute_flags}.下面的是一个替换脚本
ule = {'T':'T','a':'a','b':'b','c':'c','d':'d','e':'e','f':'f','g':'g',
'h':'h','i':'i','j':'j','k':'k','l':'l','m':'m','n':'n','o':'o',
'p':'p','q':'q','r':'r','s':'s','t':'t','u':'u','v':'v','w':'w',
'x':'x','y':'y','z':'z'}
rule['a'] = 'd',
rule['b'] = 'm'
rule['d'] = 'e'
rule['e'] = 'n'
rule['g'] = 'f'
rule['h'] = 'o'
rule['i'] = 'x'
rule['k'] = 'p'
rule['p'] = 'i'
rule['q'] = 'r'
rule['r'] = 'a'
rule['t'] = 's'
rule['u'] = 'b'
rule['w'] = 't'
rule['y'] = 'l'
rule['z'] = 'u'
rule['m'] = 'h'
rule['j'] = 'g'
rule['x'] = 'c'
rule['l'] = 'y'
rule['s'] = 't'
rule['f'] = 'w'
rule['v'] = 'k'
print rule
with open('encryption.txt', 'r') as f:
data=f.read()
print data
new_data =''
for i in xrange(0,len(data)):
if data[i].isalpha():
new_data += rule[data[i]]
else:
new_data += data[i]
print new_data
with open('result.txt', 'w') as r:
r.write(new_data)RSA 最简单模式
为什么这么说,因为
N=0x180be86dc898a3c3a710e52b31de460f8f350610bf63e6b2203c08fddad44601d96eb454a34dab7684589bc32b19eb27cffff8c07179e349ddb62898ae896f8c681796052ae1598bd41f35491175c9b60ae2260d0d4ebac05b4b6f2677a7609c2fe6194fe7b63841cec632e3a2f55d0cb09df08eacea34394ad473577dea5131552b0b30efac31c59087bfe603d2b13bed7d14967bfd489157aa01b14b4e1bd08d9b92ec0c319aeb8fedd535c56770aac95247d116d59cae2f99c3b51f43093fd39c10f93830c1ece75ee37e5fcdc5b174052eccadcadeda2f1b3a4a87184041d5c1a6a0b2eeaa3c3a1227bc27e130e67ac397b375ffe7c873e9b1c649812edcd
e=0x1
c=0x4963654354467b66616c6c735f61706172745f736f5f656173696c795f616e645f7265617373656d626c65645f736f5f63727564656c797de=1,相当于密文就是明文,测试k=0时直接16进制解密,得到
IceCTF{falls_apart_so_easily_and_reassembled_so_crudely}
这是RSA中最简单的情况,也是非常特殊的情况,有关的原理大家要回忆起上文讲的 想到原文和密文的关系
n**e ≡ c mod N
消息解密,利用密钥 d 进行解密得到明文n:
c**d ≡ n (mod N)
倒数第二简单的RSA
为啥有倒数第二了因为这个就是原理题,当初是让我们了解原理的
//题目的已知信息
N=0x1564aade6f1b9f169dcc94c9787411984cd3878bcd6236c5ce00b4aad6ca7cb0ca8a0334d9fe0726f8b057c4412cfbff75967a91a370a1c1bd185212d46b581676cf750c05bbd349d3586e78b33477a9254f6155576573911d2356931b98fe4fec387da3e9680053e95a4709934289dc0bc5cdc2aa97ce62a6ca6ba25fca6ae38c0b9b55c16be0982b596ef929b7c71da3783c1f20557e4803de7d2a91b5a6e85df64249f48b4cf32aec01c12d3e88e014579982ecd046042af370045f09678c9029f8fc38ebaea564c29115e19c7030f245ebb2130cbf9dc1c340e2cf17a625376ca52ad8163cfb2e33b6ecaf55353bc1ff19f8f4dc7551dc5ba36235af9758b
e=0x10001
phi=0x1564aade6f1b9f169dcc94c9787411984cd3878bcd6236c5ce00b4aad6ca7cb0ca8a0334d9fe0726f8b057c4412cfbff75967a91a370a1c1bd185212d46b581676cf750c05bbd349d3586e78b33477a9254f6155576573911d2356931b98fe4fec387da3e9680053e95a4709934289dc0bc5cdc2aa97ce62a6ca6ba25fca6ae366e86eed95d330ffad22705d24e20f9806ce501dda9768d860c8da465370fc70757227e729b9171b9402ead8275bf55d42000d51e16133fec3ba7393b1ced5024ab3e86b79b95ad061828861ebb71d35309559a179c6be8697f8a4f314c9e94c37cbbb46cef5879131958333897532fea4c4ecd24234d4260f54c4e37cb2db1a0
d=0x12314d6d6327261ee18a7c6ce8562c304c05069bc8c8e0b34e0023a3b48cf5849278d3493aa86004b02fa6336b098a3330180b9b9655cdf927896b22402a18fae186828efac14368e0a5af2c4d992cb956d52e7c9899d9b16a0a07318aa28c8202ebf74c50ccf49a6733327dde111393611f915f1e1b82933a2ba164aff93ef4ab2ab64aacc2b0447d437032858f089bcc0ddeebc45c45f8dc357209a423cd49055752bfae278c93134777d6e181be22d4619ef226abb6bfcc4adec696cac131f5bd10c574fa3f543dd7f78aee1d0665992f28cdbcf55a48b32beb7a1c0fa8a9fc38f0c5c271e21b83031653d96d25348f8237b28642ceb69f0b0374413308481
c=0x126c24e146ae36d203bef21fcd88fdeefff50375434f64052c5473ed2d5d2e7ac376707d76601840c6aa9af27df6845733b9e53982a8f8119c455c9c3d5df1488721194a8392b8a97ce6e783e4ca3b715918041465bb2132a1d22f5ae29dd2526093aa505fcb689d8df5780fa1748ea4d632caed82ca923758eb60c3947d2261c17f3a19d276c2054b6bf87dcd0c46acf79bff2947e1294a6131a7d8c786bed4a1c0b92a4dd457e54df577fb625ee394ea92b992a2c22e3603bf4568b53cceb451e5daca52c4e7bea7f20dd9075ccfd0af97f931c0703ba8d1a7e00bb010437bb4397ae802750875ae19297a7d8e1a0a367a2d6d9dd03a47d404b36d7defe8469根据原理,我们解密需要的是密文n 私钥d 大素数N n**d mod N就是我们要的明文,然而题中都给了,我们只需要简单跑一下脚本
#!/usr/bin/python2.7 3的跑不了 因为字符串没有decode属性方法
# -*- coding: utf-8 -*-
import math # 导入 math 模块
def normaldecode(c,d,N):
# 普通解密需要密文c 私钥d 大素数N c**d mod N
#pow(a,b,c)计算a的b次幂 如果有c则modc [2,-1]去掉0x字符
return hex(pow(c, d, N))[2:-1].decode('hex') # 再解密返回关于这个rsa再多说两句,一个是要熟悉python的模 余 次方等运算的函数,另一个就是gmpy2库,利用gmpy2破解rsa是常用的,里面有很多有关加密解密函数,用于计算私钥 解密之类的
Classicl三连
Ld hcrakewcfaxr, f hofjjlhfo hlaxuc lj f krau ev hlaxuc kxfk zfj tjui xljkeclhfoor gtk dez xfj vfooud, vec kxu pejk afck, ldke iljtju. Ld hedkcfjk ke peiucd hcrakewcfaxlh foweclkxpj, pejk hofjjlhfo hlaxucj hfd gu acfhklhfoor hepatkui fdi jeoyui gr xfdi. Xezuyuc, OrmkO3vydJCoe2qyNLmcN2qlpJXnM3SxM2Xke3q9 kxur fcu foje tjtfoor yucr jlpaou ke gcufn zlkx peiucd kuhxdeoewr. Kxu kucp ldhotiuj kxu jlpaou jrjkupj tjui jldhu Wcuun fdi Cepfd klpuj, kxu uofgecfku Cudfljjfdhu hlaxucj, Zecoi Zfc LL hcrakewcfaxr jthx fj kxu Udlwpf pfhxldu fdi guredi. F btlhn gcezd veq mtpa eyuc kxu ofsr iew.
看样子是替换密码,上https://quipqiup.com/
In cryptography, a classical cipher is a type of cipher that was used historically but now has fallen, for the most part, into disuse. In contrast to modern cryptographic algorithms, most classical ciphers can be practically computed and solved by hand. However, LyjtL3fvnSRlo2xvKIjrK2ximSHkJ3ZhJ2Hto3x9 they are also usually very simple to break with modern technology. The term includes the simple systems used since Greek and Roman times, the elaborate Renaissance ciphers, World War II cryptography such as the Enigma machine and beyond. A quick brown fox jump over the lazy dog.
有一串莫名奇妙的东西,LyjtL3fvnSRlo2xvKIjrK2ximSHkJ3ZhJ2Hto3x9 应该是移位,即凯撒加密,
然而解码没有特别的提示,base全位置爆破试试,其中一个就是flag
RSA n爆破解密
n is 966808932627497190635859236054960349099463975227350564265384373280336699853387254070662881265937565163000758606154308757944030571837175048514574473061401566330836334647176655282619268592560172726526643074499534129878217409046045533656897050117438496357231575999185527675071002803951800635220029015932007465117818739948903750200830856115668691007706836952244842719419452946259275251773298338162389930518838272704908887016474007051397194588396039111216708866214614779627566959335170676055025850932631053641576566165694121420546081043285806783239296799795655191121966377590175780618944910532816988143056757054052679968538901460893571204904394975714081055455240523895653305315517745729334114549756695334171142876080477105070409544777981602152762154610738540163796164295222810243309051503090866674634440359226192530724635477051576515179864461174911975667162597286769079380660782647952944808596310476973939156187472076952935728249061137481887589103973591082872988641958270285169650803792395556363304056290077801453980822097583574309682935697260204862756923865556397686696854239564541407185709940107806536773160263764483443859425726953142964148216209968437587044617613518058779287167853349364533716458676066734216877566181514607693882375533
e is 65537
c is 168502910088858295634315070244377409556567637139736308082186369003227771936407321783557795624279162162305200436446903976385948677897665466290852769877562167487142385308027341639816401055081820497002018908896202860342391029082581621987305533097386652183849657065952062433988387640990383623264405525144003500286531262674315900537001845043225363148359766771033899680111076181672797077410584747509581932045540801777738548872747597899965366950827505529432483779821158152928899947837196391555666165486441878183288008753561108995715961920472927844877569855940505148843530998878113722830427807926679324241141182238903567682042410145345551889442158895157875798990903715105782682083886461661307063583447696168828687126956147955886493383805513557604179029050981678755054945607866353195793654108403939242723861651919152369923904002966873994811826391080318146260416978499377182540684409790357257490816203138499369634490897553227763563553981246891677613446390134477832143175248992161641698011195968792105201847976082322786623390242470226740685822218140263182024226228692159380557661591633072091945077334191987860262448385123599459647228562137369178069072804498049463136233856337817385977990145571042231795332995523988174895432819872832170029690848
n不是很大的时候,我们可以暴力分解,网站
p q c e都知道了,那么我们就知道d,就可以解密了
#!/usr/bin/env python
# coding:utf-8
__author__ = 'zhengjim'
import gmpy2
p = gmpy2.mpz(31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928997877221)
q = gmpy2.mpz(31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928797450473)
e = gmpy2.mpz(65537)
#计算d
phi_n = (p - 1) * (q - 1) # 计算r = phin
d = gmpy2.invert(e, phi_n) # 计算私钥d ed≡1(modr) e和r互质。并求得e关于r的模反元素
print "private key:"
print d
#求密文
c = gmpy2.mpz(168502910088858295634315070244377409556567637139736308082186369003227771936407321783557795624279162162305200436446903976385948677897665466290852769877562167487142385308027341639816401055081820497002018908896202860342391029082581621987305533097386652183849657065952062433988387640990383623264405525144003500286531262674315900537001845043225363148359766771033899680111076181672797077410584747509581932045540801777738548872747597899965366950827505529432483779821158152928899947837196391555666165486441878183288008753561108995715961920472927844877569855940505148843530998878113722830427807926679324241141182238903567682042410145345551889442158895157875798990903715105782682083886461661307063583447696168828687126956147955886493383805513557604179029050981678755054945607866353195793654108403939242723861651919152369923904002966873994811826391080318146260416978499377182540684409790357257490816203138499369634490897553227763563553981246891677613446390134477832143175248992161641698011195968792105201847976082322786623390242470226740685822218140263182024226228692159380557661591633072091945077334191987860262448385123599459647228562137369178069072804498049463136233856337817385977990145571042231795332995523988174895432819872832170029690848)
print "plaintext:"
print "plaintext:"
M = pow(c,d,p*q) # 从c**d mod N(N=p*q)
print '[10进制]'+str(M)
flag = str(hex(M))[2:] # 这里截取2开始 是为了去除0x两个字符
print '[16进制]'+flag
print '[ASCII码]'+flag.decode('hex')