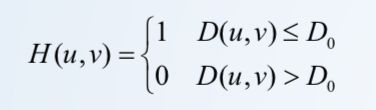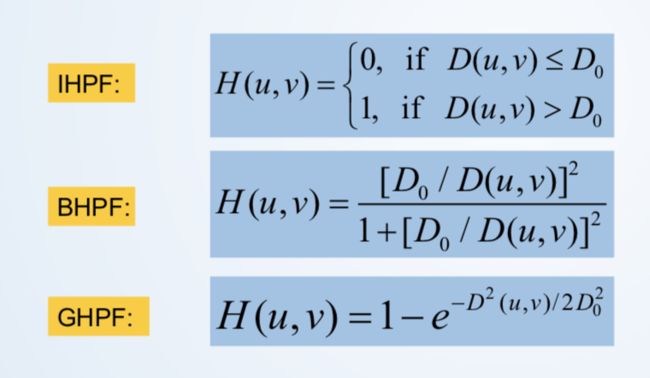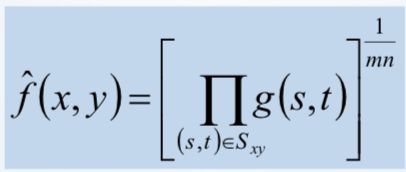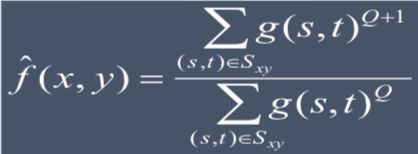啥也先不说,Lena镇个楼。
第一章 绪论
* 数字图像:能够在计算机行显示和处理的图像。
* 数字图像处理:利用计算机对图像进行分析、加工等处理,使其能够满足各种目的。
* 数字图像的特点:
1、图像中信息量大
2、图像处理数据量大
3、处理过程重复运算量大
4、处理技术综合性强
第二章 数字图像处理基础
* 人类视觉构造:
* 锥状细胞:感受光、色。对颜色敏感。
* 杆状细胞:只感受光,不能感受颜色。(缺乏得夜盲症)
* 亮度:光线的明暗程度
* 色调:色彩模式下,原色的明暗程度,如RGB下为红绿蓝三原色的明暗程度。
* 饱和度:色彩的浓度。
* 亮度对比效应:
1、同时对比效应:按对比度感觉物体量度对比。
2、马赫带效应:视觉的主管感受在亮度有变化的地方出现需要的明亮或黑暗的条纹。
* 图像数字化:将连续的模拟信号转为离散的数字信号。
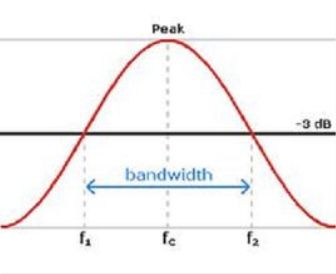
* Nyquist采样定理:
离散信号替代连续信号的条件:
1、原始信号为有限带宽信号。
2、采样频率不小于信号最高频率的2倍。
* 空间分辨率:
单位:像素/英寸,像素/厘米,像素*像素
数字图像的量化:将灰度转为整数代表。
eg 8位可以表示2^8个灰度级( 0 - 256)
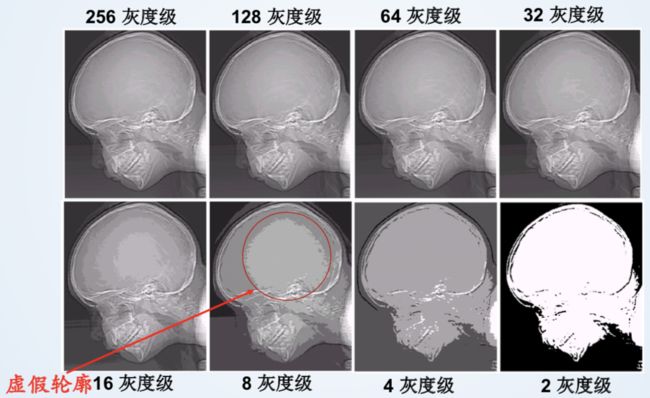
幅度分辨率:灰度级越多,该分辨率越高
(虚假轮廓:由于灰度级过少,导致颜色区别在离散化的时候被加大,导致出现类似轮廓的东西)
* 计算数字图像的数据量
像素分辨率为M*N,Q bits/像素
数据量为:M*N*Q/8 Bytes
(该量化级数:2^8)
* 数字图像分类:
1、灰度图像:在纯黑到纯白之间量化。
2、二值图像:只有黑白
3、彩色图像:如RGB图像,每个颜色通道都用相应bits表示。
* 像素间的基本关系:
* 位置关系:
* 邻接性:
邻接条件:
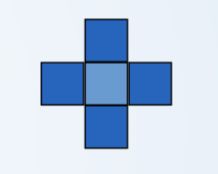
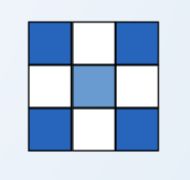
1、4相邻或8相邻
2、灰度值相近
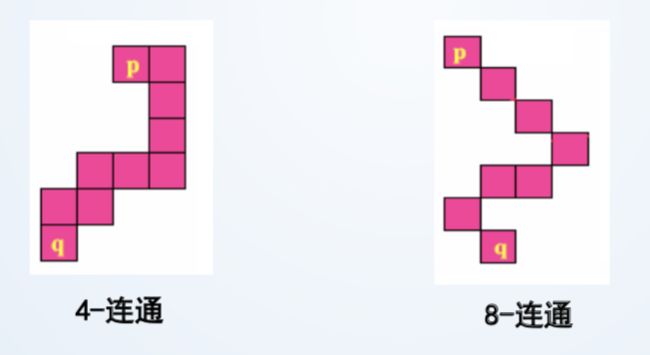
* 连通性:由邻接性产生的性质
连通集:由连通性产生
4-连通:6个
8-连通:2个
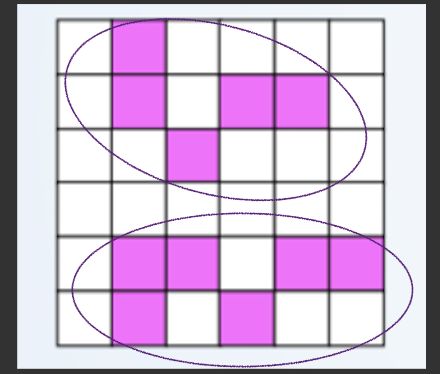
区域:R是图像的像素子集,若R为连通集,则R为一个区域。
边界:区域R中,有一个或多个领域像素不在该区域中,则该像素为其边界。(上图都是边界)
像素距离:
1、欧式距离
2、街区距离 = |x1-x2| + |y1 - y2|
3、棋盘距离= max(|x1-x2| ,|y1 - y2|)
数字图像代数运算:
应用:
加法:去除加性噪声,图像叠加。
减法:检测图像变化
乘法:抠图,改变灰度
第三章 灰度变换与空间滤波
图像增强
* 点运算:对单个像素进行变换
* 空间滤波:基于领域进行处理
* 灰度变换:
原像素->映射函数->变换后的像素
应用:
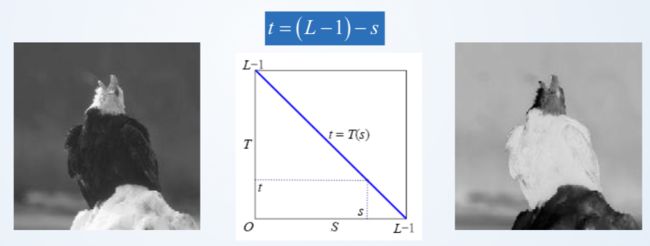
1、图像求反(底片效果)
以8bits为例:变换像素灰度 = 255 - 原像素灰度
2、线性变换(1)
扩张:将灰度集中的图像(曝光不足或者过曝)灰度动态范围拉大,加大反差,使得图像更清晰。
压缩:反之,可以柔和图像。
* 分段线性变换(2):
3、非线性变换:
目的对不同灰度范围的像素做不同程度的处理,比如暗部和高光就没必要拉大灰度值动态范围。
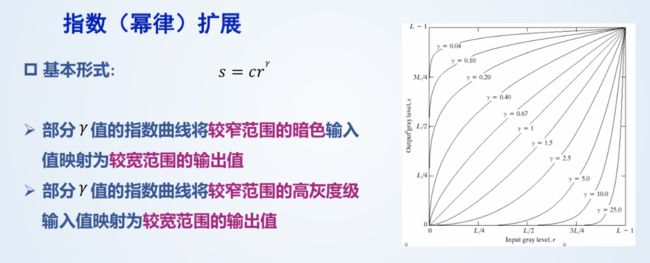
* 对数扩展:
指数扩展:
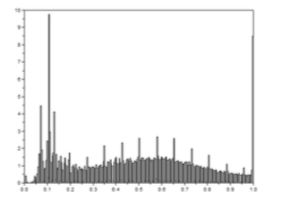
灰度直方图:反映灰度分布
横轴灰度级,纵轴像素数或者百分比
* 计算:
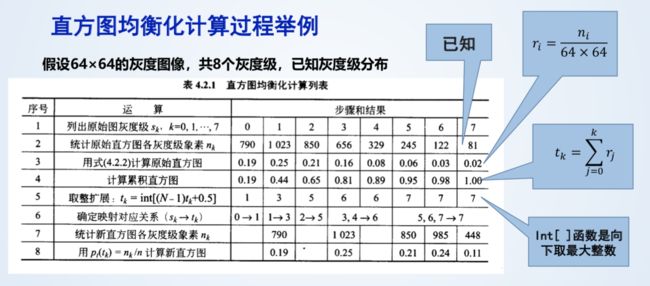
直方图均衡化
eg 练习题
灰度级 0 - 7
分布概率为:0.19, 0.25,0.21,0.16,0.08,0.06,0.03,0.02
求直方图均匀化后的像素分布:
答案:
均匀化后只有5个灰度级,1,3,5,6,7概率如下:
1:0.19,3:0.25,5:0.21,6:0.24,7:0.11
直方图规定化
简而言之,给定一个模版,使得变换后的图像像素灰度分布与模版相似。
比如该题,0灰度的占0.19接近目标模版0.2,那么就变为目标模版的灰度3。中间灰度1,2,3加起来0.62接近目标模版的0.6所以就变为5。
空域滤波
* 空域滤波器/模版:一个矩阵
* 滤波过程:
1、在图像中依次将滤波器对齐图像的像素
2、做卷积(相应像素与k乘,最后求和)
3、将结果赋值给滤波器中间位置对应的图像像素
* 边缘问题:因为滤波器无法超出图像范围,所以边缘无法滤波。
* 处理方法:
1、忽略
2、假想边缘外有与边缘灰度值一样的像素
空域滤波分类:
1、平滑滤波:平滑图像,去除高频分量,使得图像灰度值变化不那么大,同时降低噪声。
2、锐化滤波:去除低频分量,使得图像反差增大,边缘明显。
平滑滤波
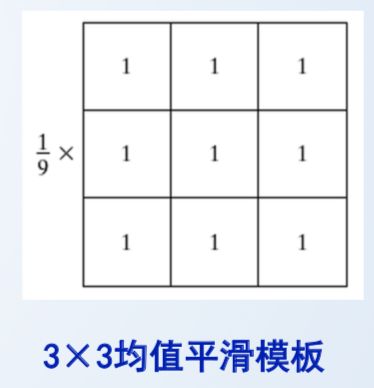
1、领域平均法
可以减少噪声,但图像也模糊了
2、加权平均法
不同位置的灰度重要性(权重)不一样,中间的最为重要,旁边的重要性降低。
3、非线性平滑滤波
锐化滤波
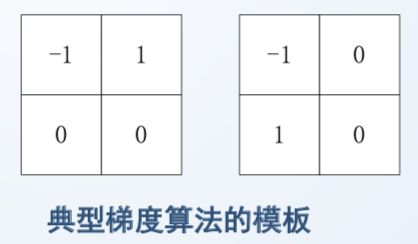
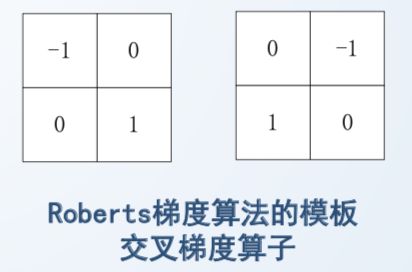
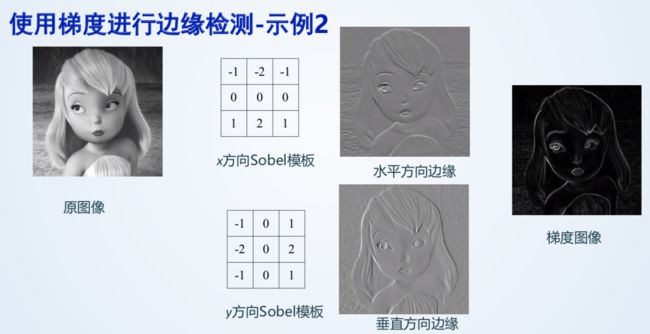
1、利用差分反映相邻像素的灰度变化大小(连续的变化程度叫微分,离散的叫差分,其实就是差值。是一个概念)
2、通过差分的出梯度。(梯度可用来检测边缘,因为边缘像素灰度变化很大)
3、锐化后的像素灰度值 = 原像素灰度值 + 锐化程度系数*梯度
实际应用:
1、
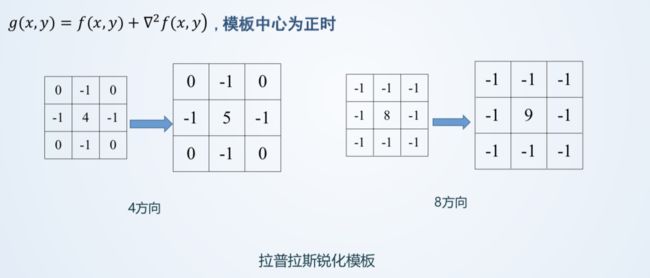
2、二阶差分模版——拉普拉斯算子
算梯度:
直接锐化:
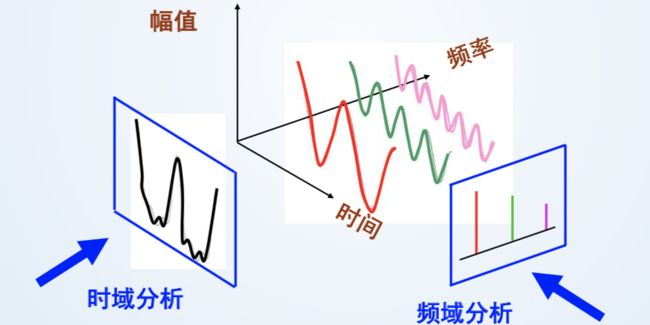
第四章 频率域滤波
> 前面我们用的矩阵滤波器是在空域对图像进行处理,现在要转到频率区域。
> 对频域不理解的同学,可以去知乎搜一搜。
> 简单介绍:
> 天才数学家傅立叶发现,任何周期信号都能用正弦函数级数表示,任何非周期信号都可以用正弦信号的加权积分表示。
> 所以这些正弦函数的分布就产生了频域的概念。
将图像二维离散傅立叶变换后:
四个角,为低频部分。中心为频率最高处。
最亮说明低频能量最高(看图片,黑大衣,背景等这些灰度变化小的像素占了大多数,它们就是低频分量)。
由于二维DFT的周期性和共轭对称性,我们可以将频率谱中心化。
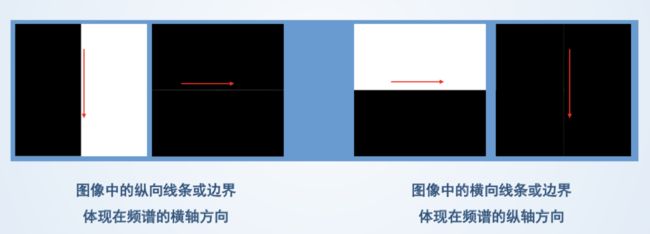
频谱图的纵横交错性:
* 频率滤波基础
步骤:
1、图像空域转频域
2、将频谱与频率滤波器相乘
3、进行傅立叶反变换得到图像
* 频域滤波分类:
1、低通滤波
2、高通滤波
3、带通和带阻滤波
4、同态滤波
* 陷波滤波器
低通滤波器
思想:噪声和边缘属于高频成分,低通,顾名思义低频通过,滤去高频。
分类:
1、理想低通滤波器
其中D0为人为确定的截止频率
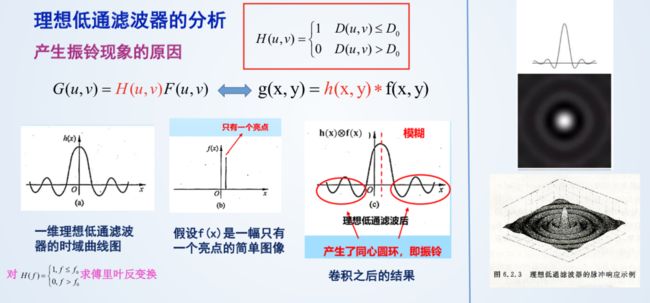
缺点:可能产生振铃现象
振铃现象产生的原因:
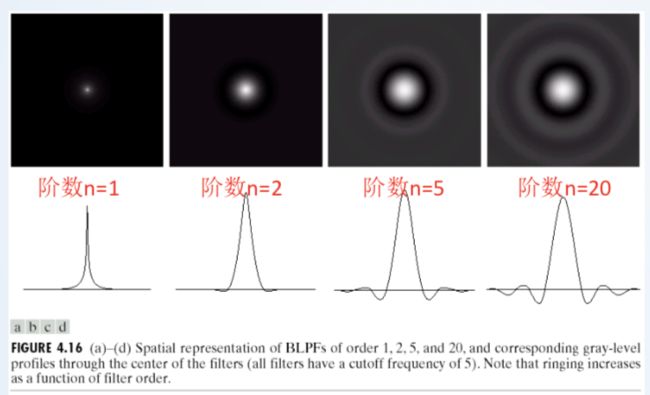
2、Butterworth低通过滤器
缺点:平滑效果不如理想低通
当Butterworth的阶数n升高时,振铃现象加大。但是优于理想低通,因为低频与高频之间是平滑过度的。而阶数越高,平滑程度越低,所以振铃现象增强。
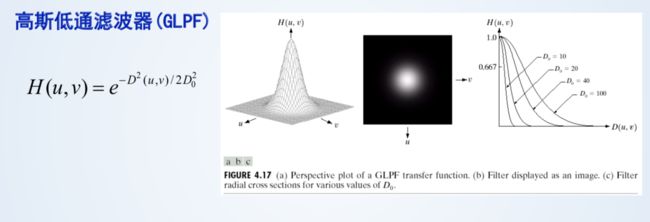
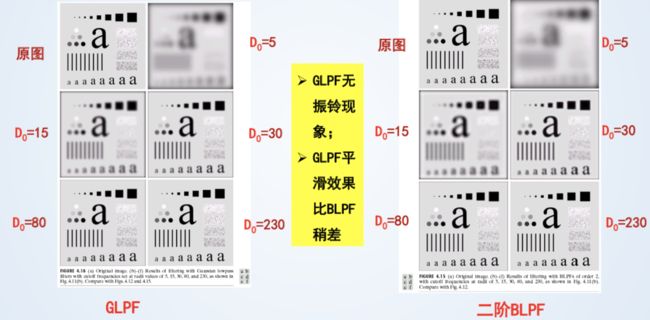
3、高斯低通过滤器(GLPF)
缺点:平滑效果不如前两个
平滑效果与截止频率的关系:
高通滤波器
高频通过,滤去低频。实现锐化。
高通滤波模版 = 1 - 低通滤波模版
效果:
同样IHPF有振铃现象。
高通滤波得到的仅仅为边缘信息,非边缘信息全变黑了。为了得到增强的锐化图像,使用高频增强滤波方法。
方法:
k * 高通滤波器 + c
k 为 > 1 的系数,c为常数
带通-带阻滤波器
同态滤波器
对于动态范围很大图像(黑的很黑,白的很白),而且细节在黑或者白的部分。
使用灰度级扩展提高反差,图像动态范围进一步加大。
压缩灰度级,动态范围变小,但是细节更加无法分辨。
此时需要将频率过滤与灰度变换结合起来——同态滤波。
* 理论基础:
图像是根据照度/反射率模型组成的。
照度:太阳光或者其他光源,一般变化较小,为低频。
反射率:由物体表面材质决定,变化大,为高频。
(举个例子,比方你望去窗外,太阳光照射所有物体的光几乎是一致的。但呈现出的不同细节等是由花草房子之类的反射率决定的)
那么,
减弱入射光i(x,y)可以缩小灰度范围。
怎强反射光r(x,y)可以提高图像对比度。
过程:
这样同态滤波器就自动的对低频的入射光进行虚弱,降低动态范围。对高频进行增强,提高对比度。
第五章 图像的复原与重建
图像退化:图像在产生、存储、传输过程中,由于设备等的不完善使得图像质量损坏。
图像复原:在图像退化模型的基础上,根据先验知识建立退化模型,再进行反运算恢复原始图像。
* 图像增强与图像复原的联系与区别
联系:都是改善图像的视觉质量
区别:增强是主观的,不考虑图像退化原因。复原是客观的,目的是最大程度还原成原图像。
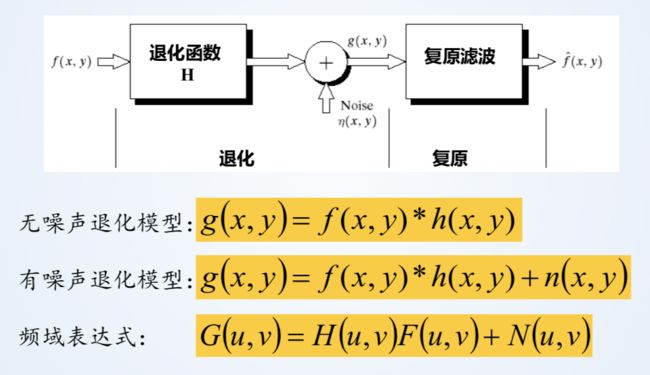
图像退化模型:
噪声模型
使用概率密度函数进行描述。
分类:
1、高斯噪声
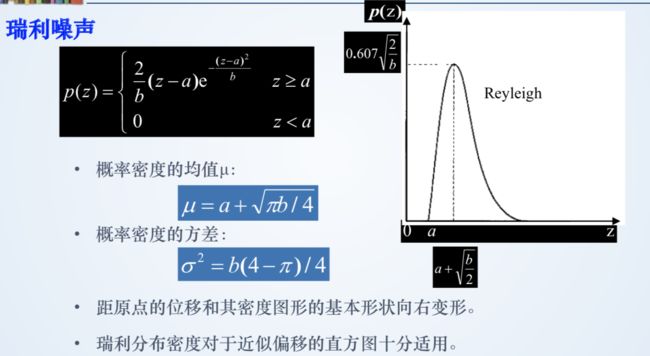
2、瑞利噪声
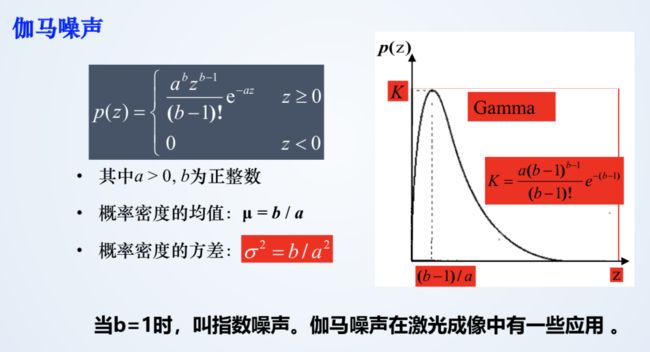
3、伽马噪声
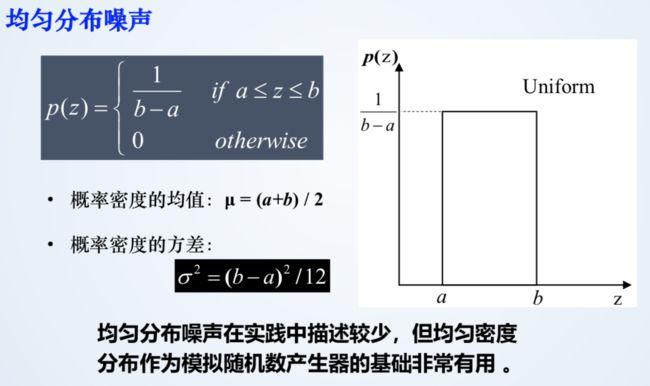
4、均匀分布噪声
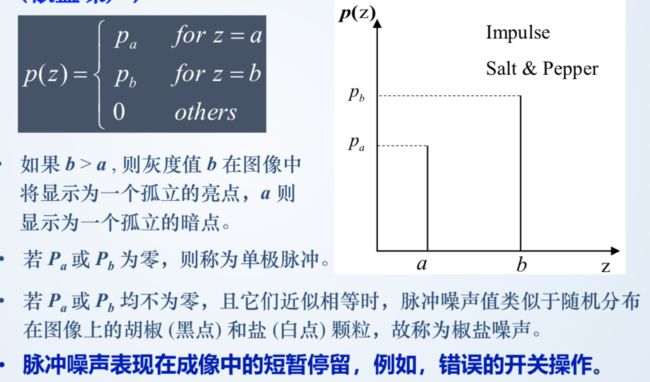
5、脉冲噪声(椒盐噪声)
6、周期噪声
一些噪声的灰度直方图:
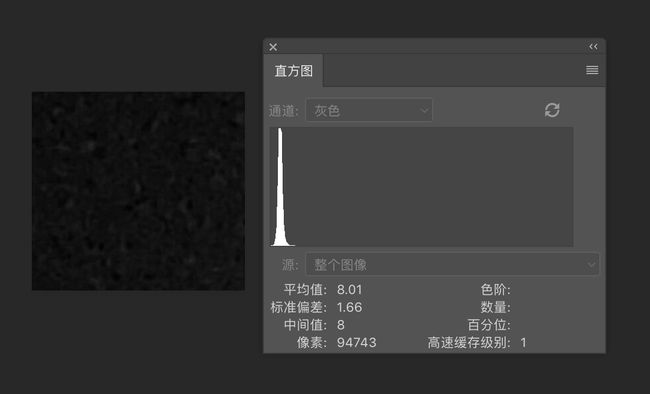
案例:
分析:
取一块变化很小的地方,绘制直方图。发现是高斯噪声模型。
噪声滤除
处理加性噪声(高斯噪声、均匀分布噪声)——空域滤波
1、算数均值滤波,做算术平均
2、几何均值滤波,做几何平均
优点:几何均值滤波图像细节保留更多,平滑程度和算术差不多。
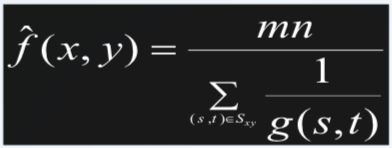
3、谐波均值滤波
处理“盐”噪声效果较好,不适用于“椒”噪声。
4、逆谐波均值滤波
Q-滤波器阶数 :
Q > 0 处理“椒”噪声
Q == 0 为算术均值滤波
Q < 0 处理“盐”噪声(Q == -1,为谐波均值滤波)
5、统计排序滤波器:
中值滤波器:相同尺寸下,比均值滤波器引起的模糊小。处理脉冲噪声很有效。但多次使用会模糊图像。
最大值滤波器:处理“椒”噪声效果好,但会从黑色物体边缘移走一些黑色色素。
最小值滤波器:处理“盐”噪声效果好,但会从白色物体边缘移走一些白色色素。
中点滤波器:计算滤波模版内最大值最小值的算术平均,即为中点值。处理高斯和均匀噪声效果最好。
6、自适应滤波器(可根据当前处理的像素信息,自行确定修复强度)
效果:
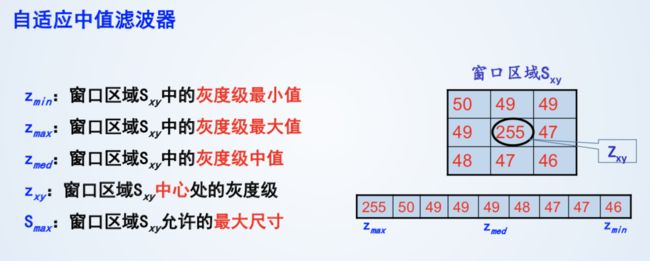
7、自适应中值滤波
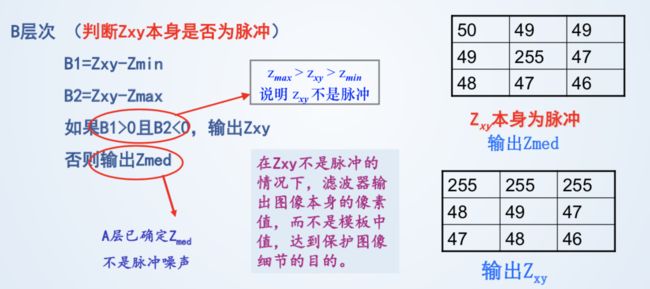
在模版内找中值,中值不是脉冲,则看中心值Zxy是不是脉冲。中心值Zxy是脉冲,则用中值代替。不是脉冲,则中心Zxy不变(优点:保存原有样子)。
如果模版已经扩展到最大了,中值还是脉冲,则输出中值。
8、逆滤波
需要先验知识,知道是什么情况的退化模型。但是噪声仍然是随机的,无法确定。
所以,一般用于信噪比高的的图像复原问题。
需要先验知识,知道是什么情况的退化模型。但是噪声仍然是随机的,无法确定。
所以,一般用于信噪比高的的图像复原问题。
如果H(u,v)取非常小的值的时候,原图像被破坏,这时候要认为干预,只在原点周围有限区域做逆滤波。
第六章 彩色图像处理
描述彩色光源3个量:
辐射量:从光源流出的能量总量。
光通量:观察者从光源感受到的能量。
亮度:主观的描述,与颜色无关,仅仅为强度。
人类对红绿蓝颜色最敏感,从而构成三基色假说,也称之为三原色。
三基色假说:三基色是一组正交基。就是说,它们相互独立,其中任何一种颜色都不能由另外两种混合而成。而其他所有颜色可由三基色按一定比例混合得到。
CIE色度图:
1、x轴:红色,y轴:绿色,蓝色: 1 - x - y;
2、边界上为全饱和的纯色,内部为混合色
3、等能量点:CIE白光标准,x = y = 1 - x - y,饱和度为0
4、任意2点的线段,都可以由线段两端的颜色混合而成。任意3点组成的三角形内的颜色,都可以由3个端点颜色混合而成。
5、等能量点到边界任意点的连线,可以定义特定色谱的所有色调。
6、该图的三原色不是固定的。
色彩模型:
1、RGB彩色模型
像素深度:每个像素所用bits数
若每个颜色用8bits,则像素深度为24
表示的颜色有2^24种
2、HSI彩色模型
这是从人对色彩的感知角度建立的彩色模型。
H(Hue)色调:观察者接受的主要颜色。
S(Saturation)饱和度:纯色背白光稀释的程度。
I(Intensity)亮度:色彩的明亮度,主观指标。
两种彩色模型利弊:
RGB适合图像生成,HSI适合图像描述。
HSI更加能够反映色彩本质,被广泛应用于计算机视觉、图像视频检索等领域。
伪彩色图像处理
根据一定的准则对灰度值赋予彩色的处理,方法就是确定灰度值与彩色的映射关系。
1、强度分层技术:不同灰度值的图像用不同颜色。
eg
2、灰度级到彩色的转换
不同的灰度值,分别确定RGB值,最后合成为彩色。
eg
全彩色图像处理
1、分别处理RGB分量图像,最后合成。
2、直接对每个像素的RGB进行处理。
色彩变换
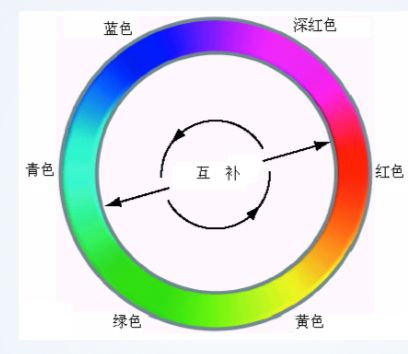
1、补色:色环上对面的颜色。
2、色彩分离开
突出图像中特殊彩色的区域
以球形为例:给定一个颜色向量(r,g,b),任何颜色(x,y,z)两者欧式距离平方小于给定距离时,则保留。
第八章 图像压缩
设n1为原始图像每个像素平均bits数,n2为压缩后的。
压缩比CR = n1 / n2
相对数据冗余RD = (n1 - n2) / n1
客观保真度标准:
图像压缩过程:
压缩:
映射:把图像由普通像素灰度矩阵的表形势转换为其他表达形式,以降低时间冗余与空间冗余。这一过程通常可逆。
量化:根据预设保真准则降低输出的精度,这一过程不可逆。
符号编码
解压缩:
符号解码
逆映射
统计编码(无损)
1、Huffman编码:数据结构已经学习。
2、算术编码:
整个消息就只有一个码字(浮点数)
缺点:对错误敏感,精度有限,需要结束符号。
编码:
解码:
3、行程编码
当图像由大面积色块组成,压缩效果好。
但灰度变化大的图像,数据量可能还会增大。(最坏情况,下一个像素都和上一个像素不一样,那么,对每一个像素都要多存一个行程1,数据量将加倍)
预测编码
根据“过去时刻”的像素值,估计当前像素值。消除相邻像素的冗余。
根据有无量化步骤来确定是否是有损压缩。
变换编码
将图像变换到另一个空间进行编码操作。
一般使用正交变换(优点):
1、正交变换可逆,不会丢失信息。
2、正交变换有能量保持性质。
3、能量重新分配与集中。
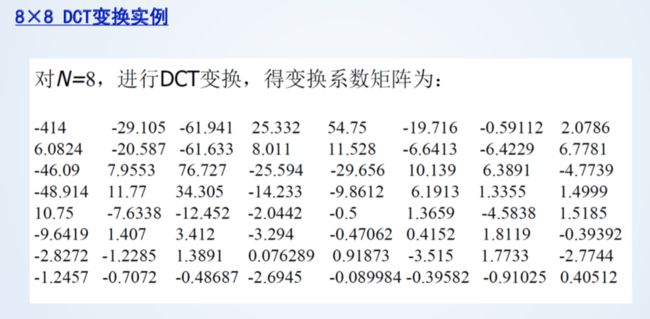
离散余弦变换(DCT):
1、携带信息能力强。
2、单片集成电路就可以实现。
3、可使图像块效应最小。
块变换编码:把图像分为大小相等且不重叠的小块,对每块进行单独编码。
块越大,块效应减弱,压缩率上升,但计算复杂度上升。
比特分配:对变换后的图像块进行截取、量化、编码。
通过保留变换后图像的一部分“重要系数”,丢弃其他部分,可以重建较高质量的图像。
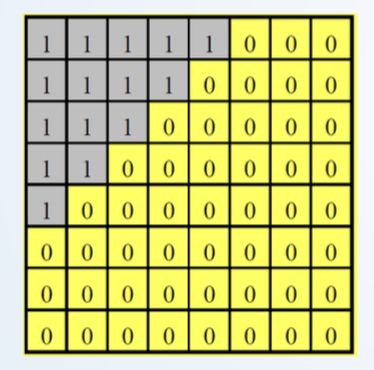
保留系数的方法
1、区域编码:
值保留能量集中部分的区域系数,其余置0。
系数保留的位置固定,所以不是对所有图像都有很好的控损能力。
2、阈值编码:
设定一个阈值,超过阈值的保留,其余舍弃。
有一定自适应能力。
但是会花费而外数据量存储超过阈值的像素位置(比如最右下脚的像素系数超过阈值,我们就得花数据记录它的位置),所以,压缩比会下降。
JEEG联合照片专家组
标准:
有损压缩:基于DCT
无损压缩:基于预测技术
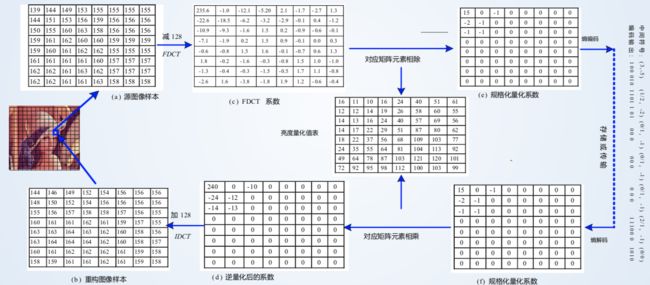
步骤:
1、使用DCT变换,得到频域。
2、用加权函数进行量化。
3、用Huffman编码对量化系数进行编码。
RGB仅支持YCbCr颜色模式,需要对以RGB模式的图像进行色彩模式转换。
Hi, Lena see u again!
Reference:
武汉大学 涂卫平教授《数字图像处理》课件