利用极小极大搜索和alpha-beta剪枝算法预测五子棋对弈落子
目录
一、问题描述
二、算法描述
三、评估函数
四、参考资料
五、源代码(Java版)
一、问题描述
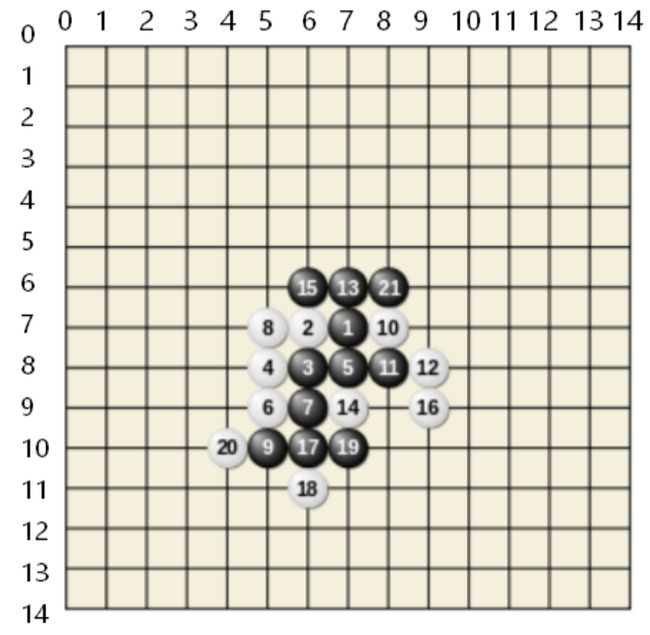
利用极小极大搜索和alpha-beta剪枝算法预测五子棋落子问题,初始棋局如图所示,AI为白子,玩家为黑子,当前由AI落子。
二、算法描述
(一)极小化极大算法:
极小化极大搜索是一种在有限的深度范围内搜索博弈树的求解方法,程序代表AI方MAX节点,目的是打败玩家,基本原理为:
(1)轮到MIN落子时,MAX节点考虑最坏的情况,即评估函数取极小值。
(2)轮到MAX落子时,MAX节点考虑最好的情况,即评估函数取极大值。
(3)搜索到叶子节点进行回溯,代表双方的对抗策略,交替使用(1)(2)规则回溯到root节点即可得到评估值。
function minimax(node, depth) // 给定初始状态和搜索深度
if node is a terminal node or depth = 0
return the evaluate value of the node //使用评估函数返回局面得分
if player’s turn // 玩家走棋,是极小节点,选择一个得分最小的走法
let val := +∞
foreach child of node
val := min(val, minimax(child, depth-1)
else AI’s turn //AI走棋,是极大节点,选择一个得分最大的走法
let val := -∞
foreach child of node
val := max(val, minimax(child, depth-1))
return val;(二)Alpha-beta算法:
极小化极大算法的搜索效率非常低下,而Alpha-beta剪枝算法能够提高搜索效率,基本原理为:
(1)alpha剪枝:任何极小层(由MIN落子)的节点的beta值都不大于其前驱节点(MAX节点)的alpha值,即搜索过程中,只要找到一个MIN节点的评估值不大于其前驱MAX节点的评估值,则可舍弃后续的搜索,这表示当前MIN节点落子对MAX是有利的。
(2)beta剪枝:任何极大层(由MAX落子)的节点的alpha值都不小于其前驱节点(MIN节点)的beta值。即搜索过程中,只要找到一个MAX节点的评估值不小于其前驱MIN节点的评估值,则可舍弃后续的搜索,这表示当前MAX节点落子对MAX是有利的。
function alphaBeta(node, alpha, beta , depth)
if node is a terminal node or depth = 0
return the evaluate value of node //使用评估函数返回局面得分
else
if AI’s turn
foreach child of node
val := alphaBeta(child, alpha, beta, depth-1)
if(val > alpha) alpha:= val
if(alpha >= beta) break
return alpha
else player’s turn
foreach child of node
val := alphaBeta(child, alpha, beta, depth-1)
if(val < beta) beta:= val
if(alpha >= beta) break
return beta三、评估函数
评估函数用于对博弈树中的叶子节点的状态进行评估,需要考虑五子棋中的基本棋型和特点,对叶子节点的棋局进行评估,给出评估值。
五子棋中的基本棋型(1代表AI落子,2代表玩家落子,0代表空位):
1. 连五:五颗同色棋子连在一起,如11111,22222
2. 活四:有两个点可以形成连五,如011110,022220
3. 冲四:有一个点可以形成连五,如011112,122220
4. 活三:可以形成活四的三点,如001110,002220
5. 眠三:只能形成冲四的三点,如001112,002221
6. 活二:能够形成活三的二点,如000110,000220
7. 眠二:能够形成眠三的二点,如000112,000221
在程序中可以某一坐标为中心,将改坐标点横竖撇捺四个方向的状态拼接为字符串,判断字符串是否包含上述的某种棋型作为判断标准。
由于算法是针对AI而言,因此在评估函数中,对玩家方赋予负值,AI方赋予正值。对于棋盘中的落子,从横竖撇捺四个方向判断形成的基本棋型,对不同的棋型赋予不同的权重,如连五代表一方胜利,赋予最大值代表AI胜利,赋予最小值代表玩家胜利。
根据棋型的重要性,划分权重如下(AI权重为正,玩家权重为负):
| 棋型 |
权重 |
| 连五 |
100000000 |
| 活四 |
10000000 |
| 冲四 |
1000000 |
| 活三 |
100000 |
| 眠三 |
10000 |
| 活二 |
1000 |
| 眠二 |
100 |
| 仅一 |
10 |
| 无 |
1 |
(一)评估函数v1
在评估过程中,计算AI所有落子位置横竖撇捺四个方向形成的棋型,得出评估值作为叶子节点的评估值。
效果:此种评估方式效果很差,仅对AI落子点进行判断过于片面,且会造成急于进攻疏于防守的局面。
(二)评估函数v2
在评估过程中,将棋盘中的所有落子的评估值相加得出最后的评估值。最终得到的评估值实际为AI落子形成的棋局评估值减玩家落子形成的棋局评估值。按此计算的目的是平衡进攻和防守。以叶子节点的评估值进行回溯,进而选择初始状态的下一步落子。
效果:评估结果较好,能够平衡进攻和防守。
四、参考资料
五子棋基本棋型及其特点
Alpha-beta剪枝
极小极大搜索方法、负值最大算法和Alpha-Beta搜索方法
五子棋的核心算法
Alpha-Beta搜索
最小-最大搜索
五子棋AI算法第四篇-启发式搜索函数
五、源代码(Java版)
Github地址:利用极小极大搜索和alpha-beta剪枝算法预测五子棋对弈落子