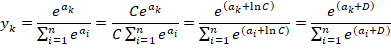深度学习笔记

持续更新...

目录

sigmoid和tanh的缺点

softmax回归

神经网络计算结构

针对问题的不同算法

one-hot表示

阶跃函数做激活函数的问题

卷积层和池化层的展开实现

图像上采样（upsampling）和下采样（downsampling）

名词解释

卷积的部分连接

神经网络的本质

Global Pooling (全局池化)

---

sigmoid和tanh的缺点

        sigmoid函数和tanh函数两者共同的缺点是，在z特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致降低梯度下降的速度。

——《吴恩达深入学习》1.3.6

---

softmax回归

softmax函数：   ：最后一层共n输出，求第k个输出的softmax值

        softmax函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。比如， 的值会超过20000， 会变成一个后面有40多个0的超大值， 的结果会返回一个表示无穷大的 inf 。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况。

softmax函数的实现可以进行如下改进：

        在进行softmax的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的D可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。

——《深度学习入门：基于Python的理论与实践》3.5.2

 

        一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果。并且，即便使用softmax函数，输出值最大的神经元的位置也不会变（比如， a的最大值是第2个元素， y 的最大值也仍是第2个元素。）。因此，神经网络在进行分类时，输出层的softmax函数可以省略。在实际的问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会被省略。

——《深度学习入门：基于Python的理论与实践》3.5.4

---

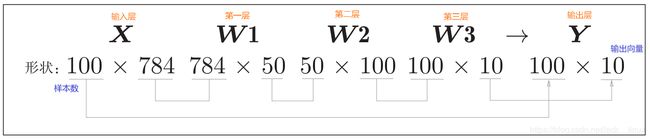
神经网络计算结构

如图所示：

图 神经网络计算结构

——《深度学习入门：基于Python的理论与实践》3.6.3

---

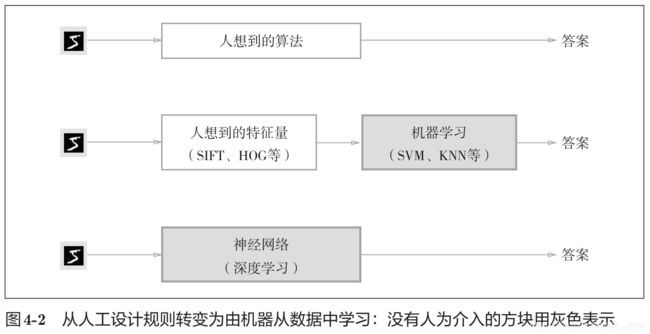
针对问题的不同算法

        如图4-2所示，神经网络直接学习图像本身。在第2个方法，即利用特征量和机器学习的方法中，特征量仍是由人工设计的，而在神经网络中，连图像中包含的重要特征量也都是由机器来学习的。

识别方法

        目前所有的深度神经网络都是利用计算机的计算能力来模拟出成千上万神经元来达到仿真的效果。然后再用模拟出来的这个神经网络，去解决真正业务的问题。所以相比一般的程序，深度神经网络多了一个仿真再处理的过程，等于是开了虚拟机再运行程序。

        传统机器学习基于统计学成功的把思考的这个问题转换为可以通过规则和逻辑来表达的方式，所以让计算机就像处理一般的程序一样，无需经过仿真环节，直接动用逻辑计算能力。

        神经网络是有史以来最美丽的编程范例之一。在传统的编程方法中，我们告诉计算机做什么，将大问题分解成计算机可轻松执行的许多精确定义的小任务。相比之下，在神经网络中，我们不需要告诉计算机如何解决我们的问题，而是让它通过观测数据学习，找出解决手头问题的办法。

—— 八大神经网络架构

—— 机器学习在干什么？

——《深度学习入门：基于Python的理论与实践》4.1.1

---

one-hot表示

将正确解标签表示为1，其他标签表示为0的表示方法称为one-hot表示，如：t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

——《深度学习入门：基于Python的理论与实践》4.2.1

---

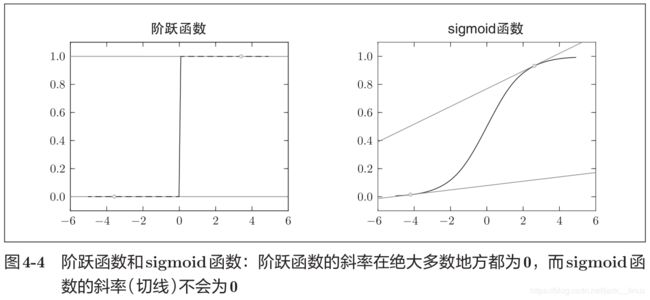
阶跃函数做激活函数的问题

        如果使用阶跃函数作为激活函数，神经网络的学习将无法进行。如图4-4所示，阶跃函数的导数在绝大多数地方（除了0以外的地方）均为0。也就是说，如果使用了阶跃函数，那么即便将损失函数作为指标，参数的微小变化也会被阶跃函数抹杀，导致损失函数的值不会产生任何变化

——《深度学习入门：基于Python的理论与实践》4.2.1

---

卷积层和池化层的展开实现

• 卷积层的展开实现：

• 池化层的展开实现：

——《深度学习入门：基于Python的理论与实践》7.4.2—7.4.4

---

图像上采样（upsampling）和下采样（downsampling）

        下采样：即采样点数减少。对于一幅 的图像来说，如果降采样系数为 ，则即是在原图中 每行每列每隔  个点取一个点组成一幅图像。

     上采样：图像放大几乎都是采用内插值方法，即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。

——图像降采样和升采样

——图像的上采样（upsampling）与下采样（subsampled）

---

名词解释

CNN —— Convolutional Neural Network，卷积神经网络

MLP —— Multi-Layer Perceptron，多层感知机 / 多层神经网络

FCN —— Fully Convolutional Network，全卷积网络

FC Layer —— Fully Connected Layer，全连接层

ROI —— Region of Interest，感兴区域

RPN —— Region Proposal Network，区域候选网络 / 区域生成网络 / 区域推荐网络

DPM —— Deformable Parts Model，可变形部件模型

SPP —— Spatial Pyramid Pooling，空间金字塔池化

IOU —— Intersection over Union，交并比

mAP —— Mean Average Precision，平均均值精度

---

卷积的部分连接

        以LeNet网络举例，如下图所示：

图 LeNet网络

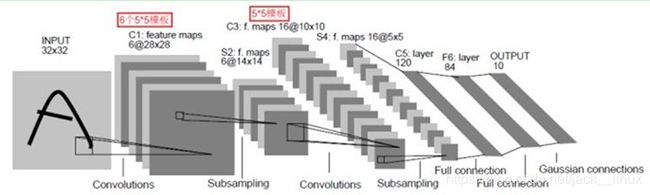
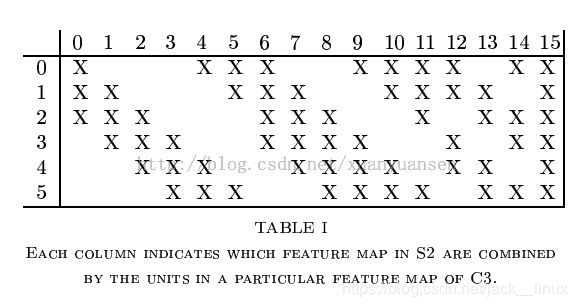
        原始图像进来以后，先进入一个卷积层C1，由6个5x5的卷积核组成，卷积出28x28的图像，然后下采样到14x14（S2）。接下来，再进一个卷积层C3，由16个5x5的卷积核组成，之后再下采样到5x5（S4）。注意，这里S2与C3的连接方式并不是全连接，而是部分连接，如下图所示：

图 部分卷积连接

        其中行代表S2层的某个节点，列代表C3层的某个节点。我们可以看出，C3-0跟S2-0,1,2连接，C3-1跟S2-1,2,3连接，后面依次类推，仔细观察可以发现，其实就是排列组合：

0 0 0 1 1 1

0 0 1 1 1 0

0 1 1 1 0 0

...

1 1 1 1 1 1

我们可以领悟作者的意图，即用不同特征的底层组合，可以得到进一步的高级特征，例如：/ + \ = ^ （比较抽象O(∩_∩)O~），再比如好多个斜线段连成一个圆等等。

最后，通过全连接层C5、F6得到10个输出，对应10个数字的概率。

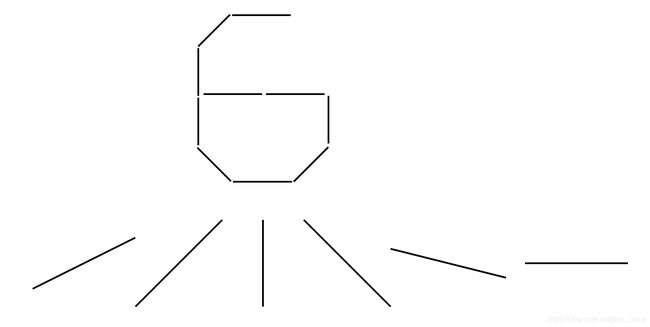
        最后说一点个人的想法哈，我认为第一个卷积层选6个卷积核是有原因的，大概也许可能是因为0~9其实能用以下6个边缘来代  表：

是不是有点道理呢，哈哈

然后C3层的数量选择上面也说了，是从选3个开始的排列组合，所以也是可以理解的。

——深度学习简介(一)——卷积神经网络

---

神经网络的本质

        神经网络由大量的节点（或称“神经元”、“单元”）相互连接构成，每个节点代表一种特定的函数，称为激励函数（Activation Function）。节点之间的连接具有特定的权重，信号经过会进行加权，代表神经网络的记忆。网络的输出则依网络的连接方式、权重值和激励函数的不同而不同。网络本身则代表对自然界某种算法或者函数的逼近，也可能是一种逻辑策略的表达。

——《行人检测：理论与实践》：81

---

Global Pooling (全局池化)

        说白了，“global pooling”就是pooling的滑窗size 和整张feature map的size一样大。这样，每个 W×H×CW×H×C 的feature map输入就会被转化为 1×1×C1×1×C 输出。因此，其实也等同于每个位置权重都为 1/(W×H)1/(W×H) 的FC层操作。等同于输入一个tensor，输出一根vector。

        “global pooling”在滑窗内的具体pooling方法可以是任意的，所以就会被细分为“global avg pooling”、“global max pooling”等。由于传统的pooling太过粗暴，操作复杂，目前业界已经逐渐放弃了对pooling的使用。替代方案 如下：

• 采用 Global Pooling 以简化计算
• 增大conv的 stride 以免去附加的pooling操作。

—— 深度学习: global pooling (全局池化)

---

前向传播的空间变换

对于神经网络：

通过如下5种对输入空间的操作，完成输入向量 —> 输出空间的变换：

1. 升维/降维
2. 放大/缩小
3. 旋转
4. 平移
5. 弯曲

        其中1，2，3是由  完成的，4是由  完成的，5是由  完成的。即用线性变换跟随着非线性变化 ，将输入空间投向另一个空间。

        以分类为例，当要分类正数、负数、零三类的时候，一维空间的直线可以找到两个超平面分割这三类（比当前空间低一维的子空间。当前空间是直线的话，超平面就是点）。

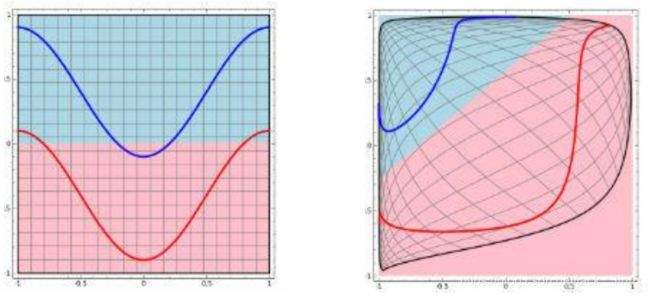
        平面的四个象限也是线性可分。但下图的红蓝两条线就无法找到一超平面去分割（当前空间为“二维平面”，故超平面为“线”）。神经网络的解决方法依旧是转换到另外一个空间下，用的是所说的5种空间变换操作。比如下图就是经过放大、平移、旋转、扭曲原二维空间后，在三维空间下就可以成功找到一个超平面分割红蓝两线 (同SVM的思路一样)。

图1 “线性不可分”问题的分类方法

        上面是一层神经网络可以做到的，如果把  当做新的输入再次用这5种操作进行第二遍空间变换的话，网络也就变为了二层。最终输出是 
        设想网络拥有很多层时，对原始输入空间的“扭曲力”会大幅增加，如下图，最终我们可以轻松找到一个超平面分割空间。

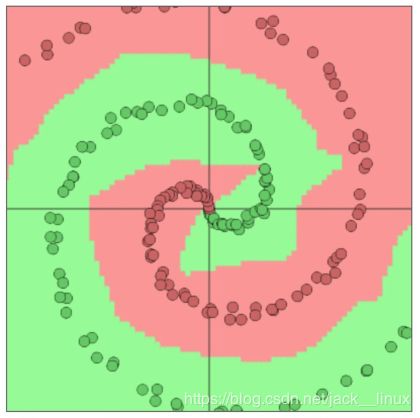图2.1 输入分类图像 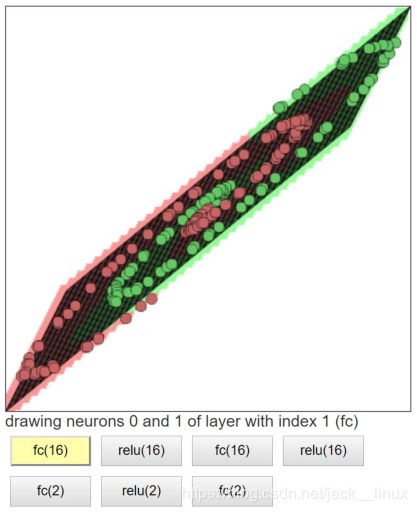图2.2 线性变换1 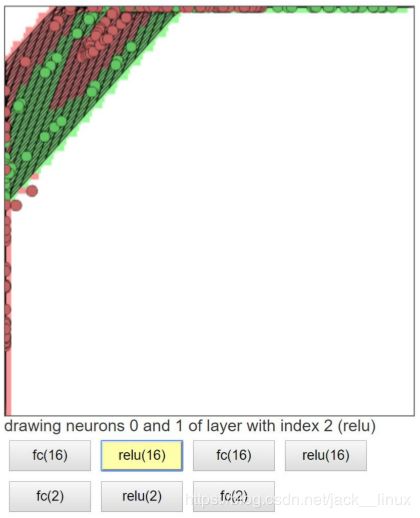图2.3 激活1 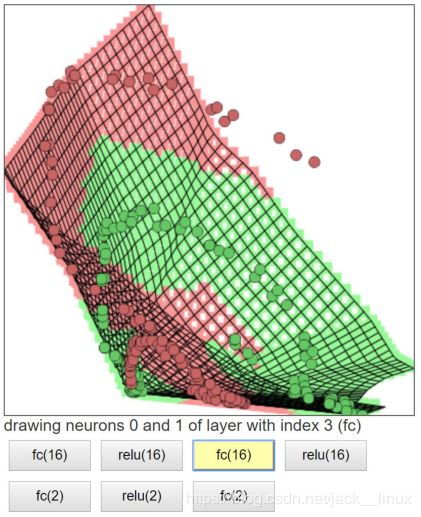图2.4 线性变换2

 

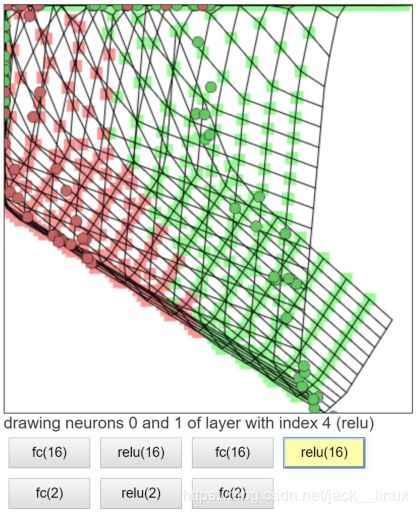图2.5 激活2 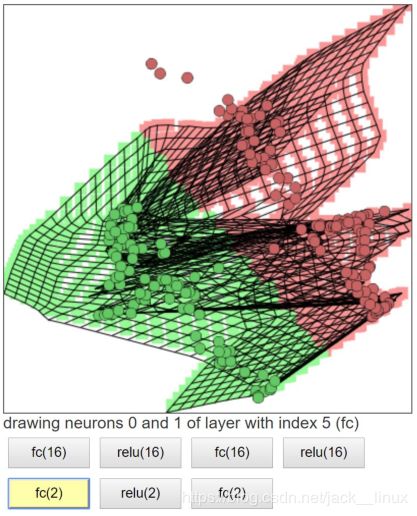图2.6 线性变换3 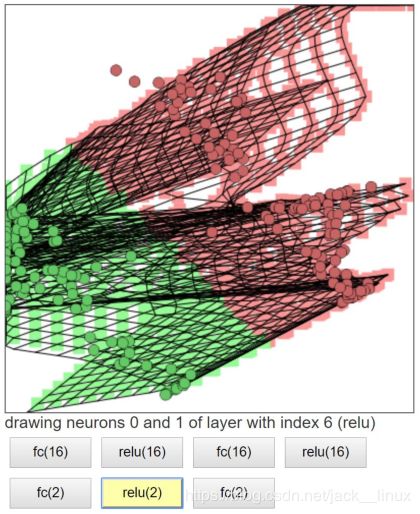图2.7 激活3 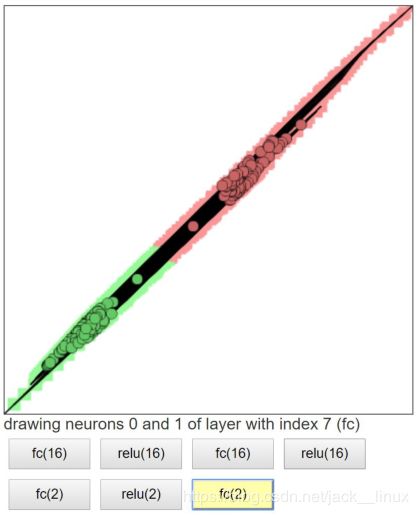图2.8 线性变换4，可分类

 

线性可分视角：神经网络的学习就是学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投向线性可分/稀疏的空间去分类/回归。
增加节点数：增加维度，即增加线性转换能力。
增加层数：增加激活函数的次数，即增加非线性转换次数。

—— 金忍，神经网络与检测识别应用

神经网络原理 DEMO：https://cs.stanford.edu/people/karpathy/convnetjs//demo/classify2d.html
http://playground.tensorflow.org

---

Batch Bormalization（BN）

该过程在 z 到 a 之间，即：

Batch Normalization

如上图所示，BN步骤主要分为4步：

1. 求每一个训练批次数据的均值
2. 求每一个训练批次数据的方差
3. 使用求得的均值和方差对该批次的训练数据做归一化，获得0-1分布。其中  是为了避免分母为0时所使用的微小正数。
4. 尺度变换和偏移：将  乘以  调整数值大小，再加上  增加偏移后得到 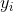 ，这里的  是尺度因子，  是平移因子。这一步是BN的精髓，由于归一化后的  基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，我们引入两个新的参数： 和 。 和  是在训练时网络自己学习得到的。

【注】： 和  同  于  一样，也属于可学习参数，使用梯度下降法更新（或其他的优化算法： Momentum、RMSprop、Adam ）。

可以去掉参数b ，（见吴恩达）