经典的卷积网络架构(一)——LeNet-5详解

LeNet-5出自论文Gradient-Based Learning Applied to Document Recognition

是一种用于手写体字符识别的非常高效的卷积神经网络

如有错误，欢迎指正！

目录

论文解读

摘要

术语

A.卷积网络

B.LeNet-5

C.损失函数

网络结构分析

代码实现

基于Tensorflow

基于Pytorch

参考博文

Github

---

引言：整理经典的卷积网络架构

---

论文解读

论文太长，就挑一些重点的概述一下。

（其实刚开始看论文会想着翻译成中文再看，但后面看习惯了也就直接对着英文半蒙半猜的边看边理解了，如果每次都翻译下来的话很浪费时间，也没有这个必要）

摘要

采用反向传播算法训练的多层神经网络是一种成功的基于梯度的学习的最佳例子。给定一个适当的网络结构，基于梯度的学习算法可以用来合成一个复杂的决策面，该决策面只需很少的预处理就可以对高维模式（如手写字符）进行分类。本文综述了各种手写体字符识别方法，并在标准手写体数字识别任务上进行了比较。专门设计用来处理二维变化的卷积神经网络优于所有其他技术。

现实生活中的文档识别系统由多个模块组成，包括字段提取、分割、识别和语言建模。一种新的学习模式，称为Graph transformer network(GTN)，允许这样的多模块系统可以整体使用基于梯度的方法进行训练，从而最大限度地减少整体的性能度量。

介绍了两种在线手写识别系统。实验证明了全局训练的优越性和图变换网络的灵活性。

文中还介绍了一种用于读取银行支票(bank check？)的Graph transformer network。它使用卷积神经网络字符识别器结合全局训练技术在企业和个人支票中提供记录准确性。它可以有效得商业化并且每天可读取数百万张支票。

术语

GT：Graph transformer 图变换

GTN： Graph transformer network

HMM： Hidden Markov model 隐马尔科夫模型

HOS： Heuristic oversegmentation 启发式超思维

K-NN： K-nearest neighbor K近邻

NN： Neural network 神经网络

OCR： Optical character recognition 光学字符识别

PCA： Principal comp onent analysis 主成分分析

RBF： Radial basis function 径向基函数

RS-SVM： Reduced-set supp ort vector method RS-支持向量机 

SDNN： Space displacement neural network

SVM： Support vector method 支持向量机 

TDNN： Time delay neural network  时延神经网络

V-SVM： Virtual supp ort vector method

 

第二部分卷积神经网络用于孤立字符识别这小节是论文的重点，主要介绍了以下三个方面得内容。

A.卷积网络

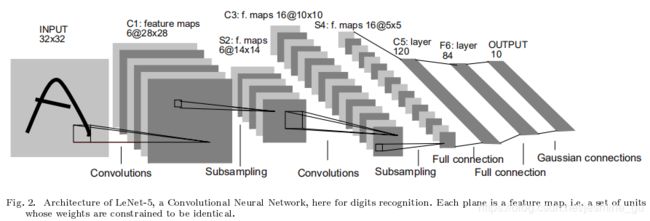
卷积网络组合了三种体系结构思想以实现一定程度的位移、缩放和形变的不变性。这三种体系结构思想分别是：局部感知野(local receptive fields)、权值共享(shared weights)、时间或者空间的下采样(spatial or tempral sub-sampling)。一个典型的用于字符识别的网络如下图2所示，文中将这个网络结构称为LeNet-5。

……

(以下三段摘自参考博文2）

一个具体的示例就是下图2 LeNet-5中的第一层，第一层隐藏层中的所有单元形成6个平面，每个是一个特征图。一个特征图中的一个单元对应有25个输入，这25个输入连接到输入层的5x5区域，这个区域就是局部感受野。每个单元有25个输入，因此有25个可训练的参数加上一个偏置。由于特征图中相邻单元以前一层中连续的单元为中心，所以相邻单元的局部感受野是重叠的。比如，LeNet-5中，水平方向连续的单元的感受野存在5行4列的重叠，之前提到过，一个特征图中所有单元共享25个权值和一个偏置，所以他们在输入图像的不同位置检测相同的特征，每一层的其他特征图使用不同的一组权值和偏置，提取不同类型的局部特征。LeNet中，每个输入位置会提取6个不同的特征。特征图的一种实现方式就是使用一个带有感受野的单元，扫描整个图像，并且将每个对应的位置的状态保持在特征图中，这种操作等价于卷积，后面加入一个偏置和一个函数，因此，取名为卷积网络，卷积核就是连接的权重。卷积层的核就是特征图中所有单元使用的一组连接权重。卷积层的一个重要特性是如果输入图像发生了位移，特征图会发生相应的位移，否则特征图保持不变。这个特性是CNN对位移和形变保持鲁棒的基础。

一旦计算出feature map,那么精确的位置就变得不重要了，相对于其他特征的大概位置是才是相关的。比如，我们知道左上方区域有一个水平线段的一个端点，右上方有一个角，下方垂直线段有一个端点，我们就知道这个数字是7。这些特征的精确位置不仅对识别没有帮助，反而不利于识别，因为对于不同的手写体字符，位置会经常变动。在特征图中降低特征位置的精度的方式是降低特征图的空间分辨率，这个可以通过下采样层达到，下采样层通过求局部平均降低特征图的分辨率，并且降低了输出对平移和形变的敏感度。LeNet-5中的第二个隐藏层就是下采样层。这个层包含了6个特征图，与前一层的6个特征图对应。每个神经元的感受野是2x2,每个神经元计算四个输入的平均，然后乘以一个系数，最后加上一个偏执，最后将值传递给一个sigmoid函数。相邻的神经元的感受野没有重叠。因此，下采样层的特征图的行和列是前一层特征图的一半。系数和偏置影响了sigmoid函数的效果。如果系数比较小，下采样层相当于对输入做了模糊操作。如果系数较大，根据偏置的值下采样层可以看成是“或”或者“与”操作。卷积层和下采样层是交替出现的，这种形式形成一个金字塔：每一层，特征图的分辨率逐渐减低，而特征图的数量逐渐增加。LeNet-5中第三个隐藏层(C3层)的每个神经元的输入可以来自前一层(S2)的多个特征图。卷积和下采样的结合的灵感来源于Hubel and Wiesel’s”简单”和”复杂”细胞的概念,虽然那个时候没有像反向传播的全局监督学习过程。下采样以及多个特征结合可以大大提高网络对几何变换的不变性。

由于所有的权值都是通过反向传播学习的，卷积网络可以看成是一个特征提取器。权值共享技术对降低参数的数量有重要的影响，同时权值共享技术减小了测试误差和训练误差之间的差距。LeNet-5包含了340908个连接，但是由于权值共享只包含了60000个可训练的参数。

B.LeNet-5

这一部分介绍LeNet-5更多的细节。

网络一共7层，不包含输入层，输入的图像尺寸是32*32的，比Mnist数据库中的28*28大。这样做的原因是希望潜在的明显的特征，比如笔画的端点或角点，能够出现在最高层特征检测器感受野的中心。

详见下面的网络结构分析。

C.损失函数

 

 

---

网络结构分析

(如上图所示) 共7层(不含输入层)，主要还是CNN的几个基本模块的组合：卷积层、池化层、全连接层

1、INPUT——输入层

输出的图像尺寸大小为32*32

2、C1——卷积层

卷积核 5*5*6

输出特征图 28*28*6 其中28=(32-5)/1+1

神经元个数 28*28*6

可训练参数 (5*5+1)*6 每个卷积核有5*5个参数和一个偏置参数，共有6个卷积核

连接数 (5*5+1)*6*28*28

C1中的每个特征图的每个单元都和输入的25个点相连，其中5*5的区域被称为感知野。每个特征图的每个单元共享25个权值和一个偏置。

3、S2——池化层

输出 14*14*6 其中14=28/2

神经元个数 14*14*6

连接数 (2*2+1)*6*14*14

4、C3——卷积层

卷积核 5*5*16

输出特征图 10*10*16 其中10=14-5+1

神经元个数 28*28*6

可训练参数 6*(3*5*5+1) +6*(4*5*5+1) +3*(4*5*5+1) +1*(6*5*5+1) 

连接数 (6*(3*5*5+1) +6*(4*5*5+1) +3*(4*5*5+1) +1*(6*5*5+1) )*10*10

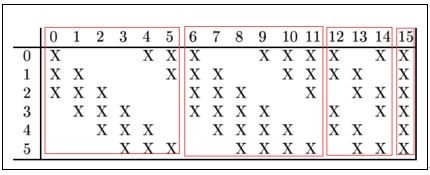
C3层比较特殊，在于它要从第一次卷积池化得到的6个特征图变成16个特征图，不是直接对应连接生成，而是通过将每个feature map连接到上层的6个或者几个特征图，以此来提取不同的特征。

为什么不把S2中的所有特征图直接连接到每个C3的特征图呢？有两个原因。

1、不完全的连接机制可以使得连接数量保持在合理的范围内；(减少了参数）

2、破坏了网络对称性。不完全的连接可以保证C3中的特征图提取到不同的特征。

 

那么具体是这样的：

C3的前6个特征图与S2的相连3个特征图相连，对应的参数是6*(3*5*5+1)

接下来的6个特征图与S2的相连4个特征图相连，对应的参数是6*(4*5*5+1)

再接下来的3个特征图与S2的不相连4个特征图相连，对应的参数是3*(4*5*5+1)

最后一个特征图与S2所有的6个特征图相连，对应的参数是1*(6*5*5+1)

 

5、S4——池化层

输出 5*5*16 其中5=10/2

神经元个数 5*5*16

连接数 (2*2+1)*16*5*5

6、C5——卷积层

卷积核 5*5*120

输出特征图 1*1*120(120维的向量) 其中1=5-5+1

可训练参数 120*(16*5*5+1)

7、F6——全连接层

可训练参数 86*(120+1)

F5层得到的输出120维向量也即F6的输入向量和权重向量点积之后，加上偏置，送入到激活函数(Sigmoid)函数输出。

8、OUTPUT——输出层

最后得到10分类，对应数字0-9。采用的是径向基函数(RBF)的网络连接方式。

输出层这一部分还不是很理解，存个疑惑。

---

代码实现

 

基于Tensorflow

# -*- coding: utf-8 -*-

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
import numpy as np
import sys
import os

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
logs_train_dir = './Model'

def weight_variable(shape):
    # 产生正态分布，标准差为0.1
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def bias_variable(shape):
    # 创建一个结构为shape矩阵也可以说是数组shape声明其行列，初始化所有值为0.1
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


def conv2d(x,W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')


def inference(images):
    # 第1层卷积
    with tf.variable_scope('conv1'):
        W_conv1 = tf.Variable(weight_variable([5, 5, 1, 6]), name="weight")
        b_conv1 = tf.Variable(bias_variable([6]), name="bias")
        h_conv1 = tf.nn.relu(conv2d(images, W_conv1) + b_conv1)
    # print(np.shape(h_conv1))
    # 第2层池化
    with tf.variable_scope('pool2'):
        h_pool2 = max_pool_2x2(h_conv1)
    # print(np.shape(h_pool2))

    # 第3层卷积
    with tf.variable_scope('conv3'):
        W_conv3 = tf.Variable(weight_variable([5, 5, 6, 16]), name="weight")
        b_conv3 = tf.Variable(bias_variable([16]), name="bias")
        h_conv3 = tf.nn.relu(conv2d(h_pool2, W_conv3) + b_conv3)
    # print(np.shape(h_conv3))
    # 第4层池化
    with tf.variable_scope('pool4'):
        h_pool4 = max_pool_2x2(h_conv3)
    # print(np.shape(h_pool4))
    h_pool4_flat = tf.reshape(h_pool4, [-1, 7 * 7 * 16])

    # 5\6\7全连接层
    with tf.variable_scope('fc5'):
        W_fc5 = weight_variable([7 * 7 * 16, 120])
        b_fc5 = bias_variable([120])
        h_fc5 = tf.nn.relu(tf.matmul(h_pool4_flat, W_fc5) + b_fc5)

    with tf.variable_scope('fc6'):
        W_fc6 = weight_variable([120, 84])
        b_fc6 = bias_variable([84])
        h_fc6 = tf.nn.relu(tf.matmul(h_fc5, W_fc6) + b_fc6)

    with tf.variable_scope('out'):
        W_out = weight_variable([84, 10])
        b_out = bias_variable([10])
        h_out = tf.nn.softmax(tf.matmul(h_fc6, W_out) + b_out)

    # h_out_drop = tf.nn.dropout(h_out, 0.5)
    return h_out

x = tf.placeholder(tf.float32, [None, 28*28])
y_ = tf.placeholder(tf.float32, [None, 10])
x_image = tf.reshape(x, [-1, 28, 28, 1])

y_conv = inference(x_image)

# 定义损失函数和学习步骤
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv), reduction_indices=[1]))   # 交叉熵
train_step = tf.train.AdamOptimizer(1e-3).minimize(cross_entropy)   # 用Adam优化器

correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))


summary_op = tf.summary.merge_all()
sess = tf.InteractiveSession()
saver = tf.train.Saver()
sess.run(tf.global_variables_initializer())
train_writer = tf.summary.FileWriter(logs_train_dir, sess.graph)

for i in range(2000):
    batch = mnist.train.next_batch(50)
    if i % 100 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1]})
        print("step %d, training accuracy %g" % (i, train_accuracy))
        # summary_str = sess.run(summary_op)
        # train_writer.add_summary(summary_str, i)
    train_step.run(feed_dict={x: batch[0], y_: batch[1]})
checkpoint_path = os.path.join(logs_train_dir, 'thing.ckpt')
saver.save(sess, checkpoint_path)
print("test accuracy %g" % accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

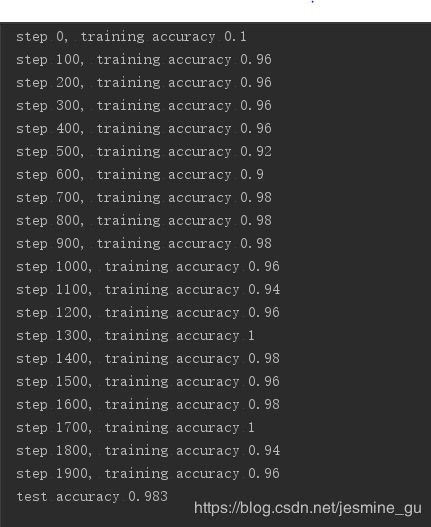
实验结果(迭代2000次)

 

基于Pytorch

最近打算学一下Pytorch，所以看了一点基础教程，直接上手实践吧。

 

 

 

参考博文

1.网络解析（一）：LeNet-5详解

2.LeNet论文的翻译与CNN三大核心思想的解读

---

感觉整个整理下来花的时间比预期的多了很多，那就慢慢来吧。

所有的论文和笔记会一点点合并整理到我的Github。

Github