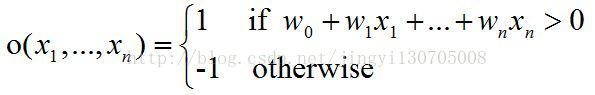感知器及其训练法则
1. 什么是感知器
感知器以一个实数值向量作为输入,计算这些输入的线性组合,然后如果结果大于某个阈值,就输出1,否则输出-1。更准确地,如果输入为x1到xn,那么感知器计算的输出为:
其中wi为权值,用来决定输入xi对感知器输出的贡献率。为了简化表示,我们假想有一个附加的常量输入x0=1,那么我们就可以写成向量形式:
这样,感知器可以表示成下图:
图1 感知器
学习一个感知器意味着选择w1,...,wn的值,接下来我们就来介绍一下常用的感知器训练法则。
2. 感知器的训练法则
对于单个感知器的权值,已经有几个常用算法,这里给出两种:感知器法则、delta法则。这两种算法可以保证收敛到可接受的假设,只是在不同的条件下收敛到的假设略有不同。
2.1 感知器法则
为了得到可接受的权向量,感知器法则是从随机的权值开始,然后反复地对每一个训练样例应用这个感知器,在当前感知器误分类样例时修改感知器的权值。重复这个过程,直到感知器正确分类所有的训练样例。修改权值的法则如下:
其中:
这里,wi为每次迭代时xi对应的权值,△wi为每次wi的修正值,t是当前训练样本的目标输出,o是感知器的输出,η是学习速率。学习速率的作用是缓和每一步调整权的程度,它通常被设为一个小的数值(例如0.1),而且有时会使其随着权调整次数的增加而衰减。
事实证明,在经过有限次地使用感知器训练法则后,上面的训练过程会收敛到一个正确分类所有训练样例的权向量,前提是训练样例线性可分,并且使用了充分小的η。如果数据不是线性可分的,那么不能保证训练过程收敛。
2.2 delta法则
当训练样本是非线性可分时,感知器训练法则就束手无策了,为了解决这个问题,提出了delta法则。delta法则的关键思想是使用梯度下降来搜索可能的权向量假设空间,以找到最佳拟合训练样本的权向量。delta训练法可以理解成一个无阈值的感知器,即一个线性单元,其输出o可表示为:
为了推导线性单元的权值学习法则,先指定一个度量标准来衡量假设(权向量)相对于训练样例的训练误差,其中最常用的度量标准为:
其中,D是训练样例的集合,td是样例d的目标输出,od是线性单元对样例d的输出。
接下来,我们的目的就是确定一个权向量使得E达到最小。梯度下降法从任意的初始向量开始,然后以很小的步伐反复修改这个向量。每一步都沿误差曲面产生最陡峭下降的方向修改权向量,继续这个过程直到得到全局的最小误差点。
那么怎么计算最陡峭下降的方向呢?答案是通过计算E关于向量w的偏导数来确定,实际上这个下降最快的方向就是使E上升最快的方向的反方向。既然梯度确定了E最陡峭上升的方向,那么梯度下降的训练法则为:
其中:
这里η是一个正数的学习速率,它决定梯度下降搜索中的步长。公式的负号是因为我们想让权向量向E下降的方向移动。这个训练法则也可以写成它的分量形式:
其中:
这样,公式变得很清楚,最陡峭的下降可以按照∂E/∂wi改变w中的每一个分量wi来实现。现推导每个梯度分量的公式,如下:
最终,梯度下降权值更新公式为:
梯度下降是一种重要的通用学习范型,在实践中会遇到这样两个问题:(1)有时收敛过程可能非常慢(它可能需要数千步的梯度下降);(2)如果在误差曲面上有多个局部极小值,那么不能保证这个过程会找到全局最小值。为了缓解这些问题,提出一种随机梯度下降。随机梯度下降的思想是根据每一个单独样例的误差增量计算权值更新,修改后的公式为:
标准的梯度下降与随机梯度下降的区别:
a. 标准的梯度下降是在权值更新前对所有样例汇总误差,而随机梯度下降的权值是通过考查每个训练实例来更新的;
b. 在标准梯度下降中,权值更新的每一步对多个样例求和,这需要大量的计算,另一方面由于使用的是真正的梯度,标准的梯度下降对于每一次权值的更新经常使用比随机梯度下降较大的步长;
c. 由于随机梯度下降使用不同的▽Ed(w)而不是▽E(w)来引导搜索,所以随机梯度下降可能避免陷入这些局部极小值中。
3. 小结
本文讨论了迭代学习感知器权值的两个相似的算法,感知器法则和delta法则(随机梯度下降)。这两个算法的关键差异是感知器法则是根据阈值化的感知器输出误差更新权值,而delta法则则是根据输入的非阈值化线性组合的误差来更新权值。另一个差异是感知器法则经过有限次地迭代就可以收敛到一个能理想分类的假设,但前提是训练样例线性可分;随机梯度下降无论样例是否线性可分都会收敛,只是需要的时间很长。