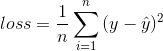常用Loss总结

1. BCELoss

用于二分类任务，二值交叉熵(Binary Cross Entropy)。

公式如下，其中y是真实值，是预测值：

使用方式如下：

class torch.nn.BCELoss


Examples::

        >>> m = nn.Sigmoid()
        >>> loss = nn.BCELoss()
        >>> input = torch.randn(3, requires_grad=True)  
        >>> target = torch.empty(3).random_(2)  # 0 或者 1
        >>> output = loss(m(input), target)
        >>> output.backward()

 2. CELoss

用于多分类任务，交叉熵(Cross Entropy)。

公式如下，其中y是真实值，是预测值：

使用方式如下：

class torch.nn.CrossEntropyLoss


It is useful when training a classification problem with `C` classes.
The `input` is expected to contain scores for each class.

Examples::

        >>> loss = nn.CrossEntropyLoss()
        >>> input = torch.randn(3, 5, requires_grad=True)
        >>> target = torch.empty(3, dtype=torch.long).random_(5)
        >>> output = loss(input, target)
        >>> output.backward()

3. MSELoss

计算均方误差 Mean Squared Error (squared L2 Norm)。

公式如下，其中y是真实值，是预测值：

class torch.nn.MSELoss

Creates a criterion that measures the mean squared error (squared L2 norm) between
    each element in the input `x` and target `y`.

Examples::

        >>> loss = nn.MSELoss()
        >>> input = torch.randn(3, 5, requires_grad=True)
        >>> target = torch.randn(3, 5)
        >>> output = loss(input, target)
        >>> output.backward()

 

类别极度不均衡情况

4. FocalLoss

https://www.cnblogs.com/king-lps/p/9497836.html

https://arxiv.org/pdf/1708.02002.pdf

二分类任务，Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

Focal loss 修改自 cross entropy loss for binary classfication （严格来讲是BCE，而不是CE），二值交叉熵：

可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。

 

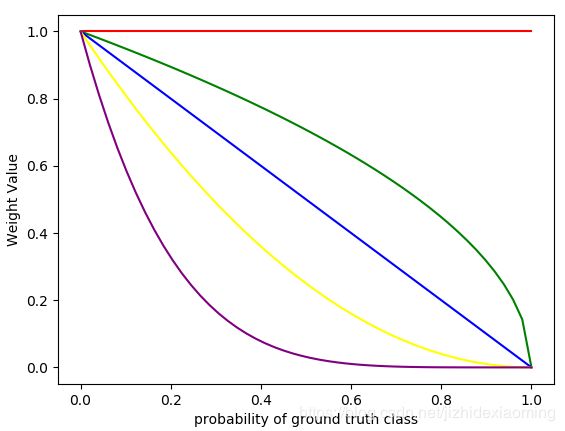
公式4是y = 1时的Focal loss和预测概率p之间关系。其中，gamma=0时，即为二值交叉熵函数。Focal loss只是在原有函数上加个权重，我们可以单独画出y = 1的权重函数图像：

画图所用到的代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 1)
y1, y2, y3, y4, y5 = (1-x)**0, (1-x)**0.5, (1-x)**1, (1-x)**2, (1-x)**5
plt.plot(x, y1, 'red')
plt.plot(x, y2, 'green')
plt.plot(x, y3, 'blue')
plt.plot(x, y4, 'yellow')
plt.plot(x, y5, 'purple')
# plt.title('line chart')
plt.xlabel('probability of ground truth class')
plt.ylabel('Weight Value') 
plt.show()

生成的权重图像：

 

注意：用权重函数，加权BCELoss，则生成论文中的函数图像。由上图可知，其中gamma=2时，权重函数是个单调下降函数，预测的概率值较小时（即为难样本），Focal Loss所加的权重较大，使得整体loss变大，突出难样本；预测值较大时，Focal Loss所加的权重较小（即为易样本），Focal Loss所加的权重较小，使得整体loss变小，这不要紧，因为预测值较大，我们就是希望loss较小。

 

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 1)
y1, y2, y3, y4, y5 = (1-x)**0 * (-np.log(x)), (1-x)**0.5 * (-np.log(x)), (1-x)**1 * (-np.log(x)), (1-x)**2 * (-np.log(x)), (1-x)**5 * (-np.log(x))
plt.plot(x, y1, 'red')
plt.plot(x, y2, 'green')
plt.plot(x, y3, 'blue')
plt.plot(x, y4, 'yellow')
plt.plot(x, y5, 'purple')
# plt.title('line chart')
plt.xlabel('probability of ground truth class')
plt.ylabel('Focal loss') 
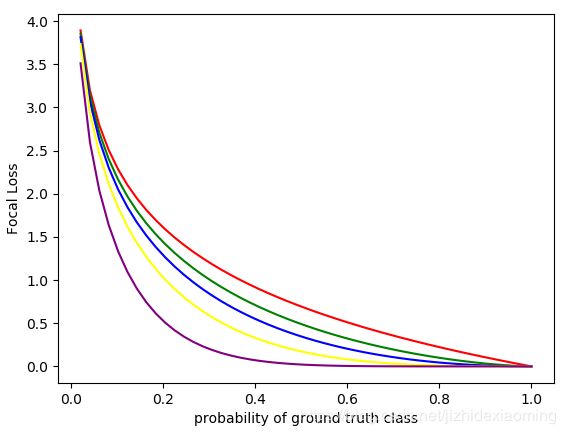
plt.show()

 

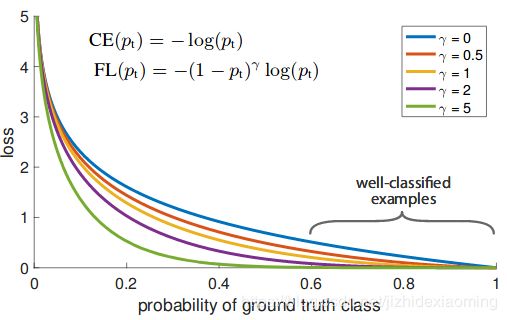
备注：论文中的图像如下

 

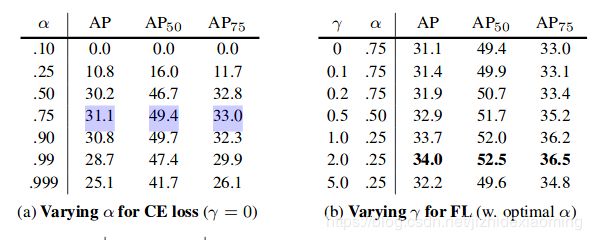
此外，加入平衡因子alpha，用来平衡正负样本本身的比例不均：文中alpha取0.25。用到缺陷检测时，有缺陷的样本非常少，同样可以加入平衡因子alpha。 In practice α may be set by inverse class fre-quency or treated as a hyperparameter to set by cross validation. 即alpha可以设置与样本数成反比，也可以视为一个超参数。

作为正类的有缺陷样本数较少，按照论文的意思应该是alpha大于0.5才对，那是没有情况下才是这样的，因为Focal Loss受两个调节因子影响，不能但看一个，所以这个参数只是试出来的。 

从论文中的实验部分可以得到验证，左边是只有alpha, 没有加权的，所以apha=0.75时最好。

 

 

5. DiceLoss

https://www.aiuai.cn/aifarm1159.html

较适用于样本极度不均的情况，公式如下。

后面部分是A和B相似度度量。其中上面分子是矩阵A和B逐个元素相乘，再求和。分母是矩阵分别求和，再相加。对于二分类问题，GT 分割图是只有 0, 1 两个值的，因此 可以有效的将在 Pred 分割图中未在 GT 分割图中激活的所有像素清零，即不管背景像素，只关注要检测的部分. 对于激活的像素，主要是惩罚低置信度的预测，较高值会得到更好的 Dice 系数.

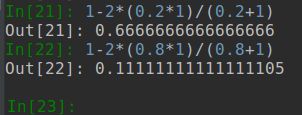
验证结果，预测值为0.2比0.8的loss更大，正好符合：当前类为正类，预测值越小，对应的loss越大。注意diceLoss是不管负类的。

import torch.nn as nn
import torch.nn.functional as F

class SoftDiceLoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(SoftDiceLoss, self).__init__()
 
    def forward(self, logits, targets):
        num = targets.size(0)
        smooth = 1
        
        probs = F.sigmoid(logits)
        m1 = probs.view(num, -1)
        m2 = targets.view(num, -1)
        intersection = (m1 * m2)
 
        score = 2. * (intersection.sum(1) + smooth) / (m1.sum(1) + m2.sum(1) + smooth)
        score = 1 - score.sum() / num
        return score

 

待续。。。