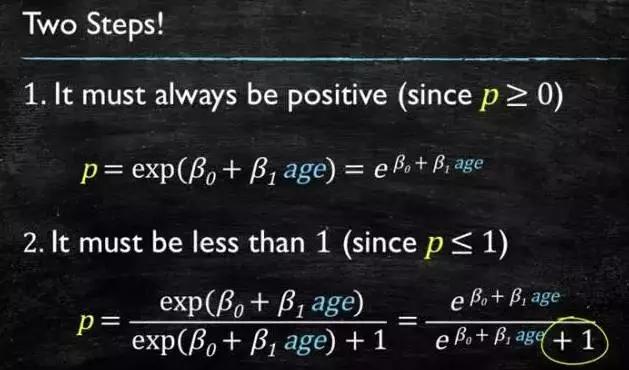图解十大经典机器学习算法入门
弱人工智能近几年取得了重大突破,悄然间,已经成为每个人生活中必不可少的一部分。以我们的智能手机为例,看看到底温藏着多少人工智能的神奇魔术。
下图是一部典型的智能手机上安装的一些常见应用程序,可能很多人都猜不到,人工智能技术已经是手机上很多应用程序的核心驱动力。
图1 智能手机上的相关应用
传统的机器学习算法包括决策树、聚类、贝叶斯分类、支持向量机、EM、Adaboost等等。这篇文章将对常用算法做常识性的介绍,没有代码,也没有复杂的理论推导,就是图解一下,知道这些算法是什么,它们是怎么应用的。
人工智能领域知识面广泛,推荐专注于人工智能在线教育的平台—深蓝学院。深蓝学院由中科院自动化所毕业博士团队创建,虽成立半年,但在业界已颇具口碑。
决策树
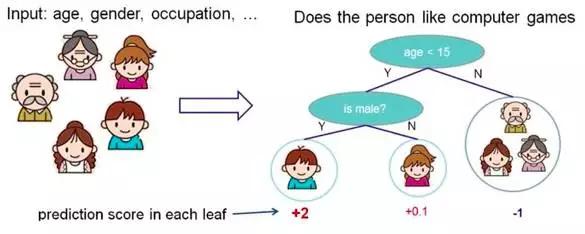
根据一些 feature(特征) 进行分类,每个节点提一个问题,通过判断,将数据分为两类,再继续提问。这些问题是根据已有数据学习出来的,再投入新数据的时候,就可以根据这棵树上的问题,将数据划分到合适的叶子上。
图2 决策树原理示意图
随机森林
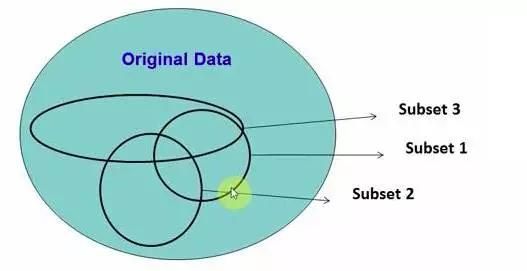
在源数据中随机选取数据,组成几个子集:
图3-1 随机森林原理示意图
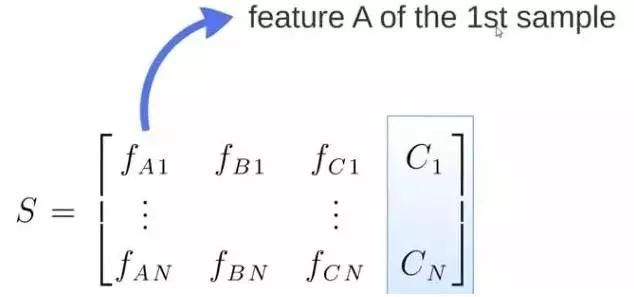
S矩阵是源数据,有1-N条数据,A、B、C 是feature,最后一列C是类别:
由S随机生成M个子矩阵:
这M个子集得到 M 个决策树:将新数据投入到这M个树中,得到M个分类结果,计数看预测成哪一类的数目最多,就将此类别作为最后的预测结果。
图3-2 随机森林效果展示图
逻辑回归
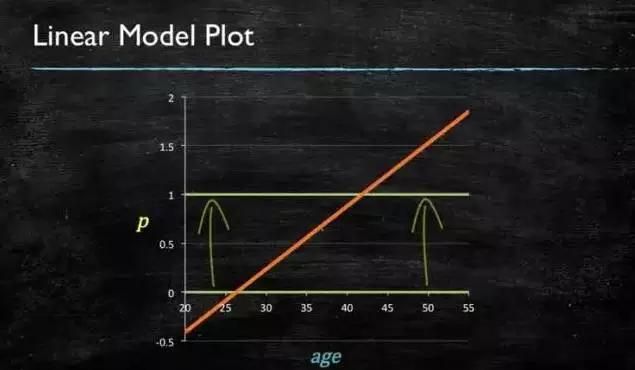
当预测目标是概率这样的,值域需要满足大于等于0,小于等于1的,这个时候单纯的线性模型是做不到的,因为在定义域不在某个范围之内时,值域也超出了规定区间。
图4-1 线性模型图
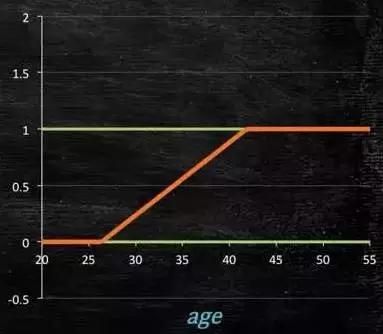
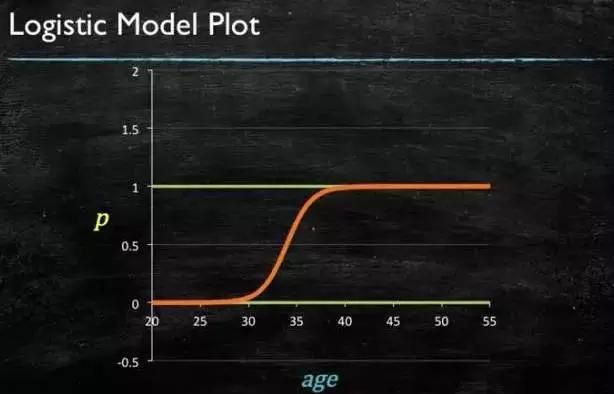
所以此时需要这样的形状的模型会比较好:
图4-2
那么怎么得到这样的模型呢?
这个模型需要满足两个条件 “大于等于0”,“小于等于1” 。大于等于0 的模型可以选择绝对值,平方值,这里用指数函数,一定大于0;小于等于1 用除法,分子是自己,分母是自身加上1,那一定是小于1的了。
图4-3
再做一下变形,就得到了 logistic regressions 模型:
图4-4
通过源数据计算可以得到相应的系数了:
图4-5
图4-6 LR模型曲线图
支持向量机
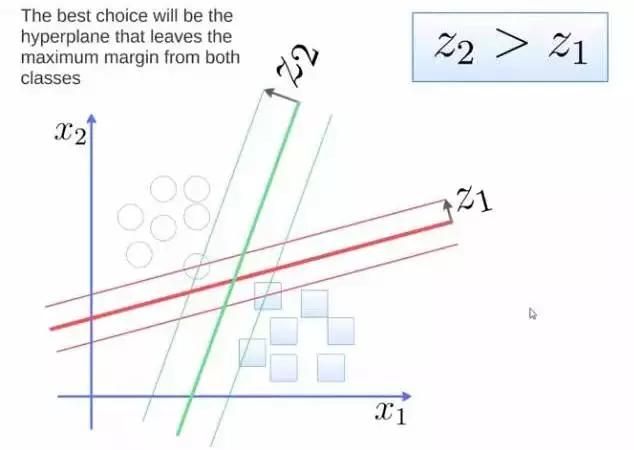
要将两类分开,想要得到一个超平面,最优的超平面是到两类的 margin 达到最大,margin就是超平面与离它最近一点的距离,如下图,Z2>Z1,所以绿色的超平面比较好。
图5 分类问题示意图
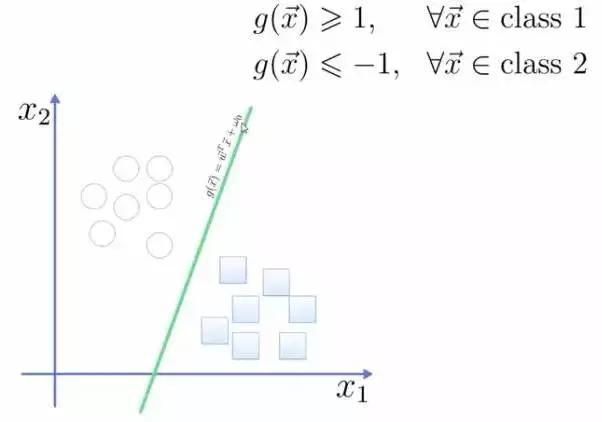
将这个超平面表示成一个线性方程,在线上方的一类,都大于等于1,另一类小于等于-1:
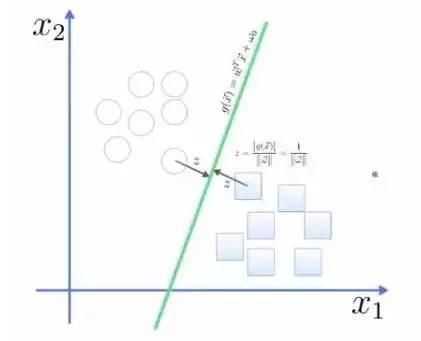
点到面的距离根据图中的公式计算:
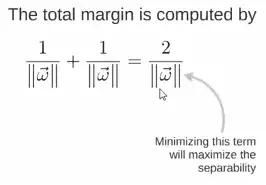
所以得到total margin的表达式如下,目标是最大化这个margin,就需要最小化分母,于是变成了一个优化问题:
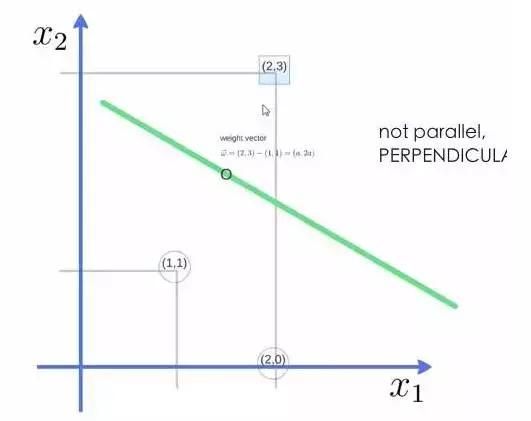
举个例子,三个点,找到最优的超平面,定义了 weight vector=(2,3)-(1,1):
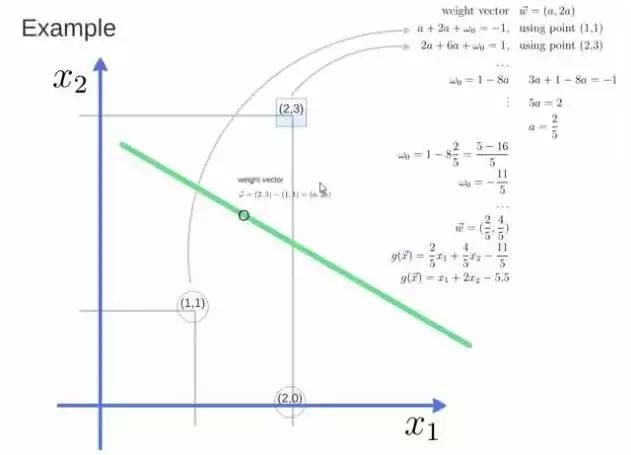
得到weight vector为(a,2a),将两个点代入方程,代入(2,3)另其值=1,代入(1,1)另其值=-1,求解出 a 和 截矩 w0 的值,进而得到超平面的表达式。
a求出来后,代入(a,2a)得到的就是support vector,a和w0代入超平面的方程就是support vector machine。
朴素贝叶斯
举个在 NLP 的应用:给一段文字,返回情感分类,这段文字的态度是positive,还是negative:
图6-1 问题案例
为了解决这个问题,可以只看其中的一些单词:
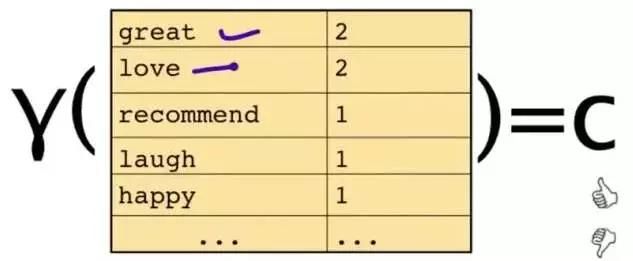
这段文字,将仅由一些单词和它们的计数代表:
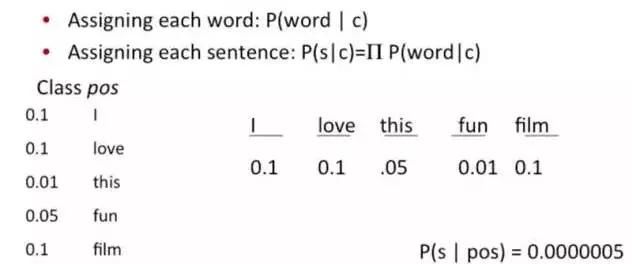
原始问题是:给你一句话,它属于哪一类 ?通过bayes rules变成一个比较简单容易求得的问题:
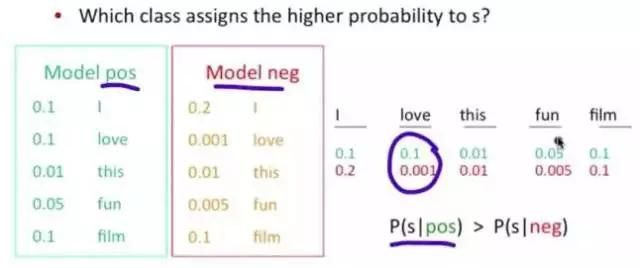
问题变成,这一类中这句话出现的概率是多少,当然,别忘了公式里的另外两个概率。例子:单词“love”在positive的情况下出现的概率是 0.1,在negative的情况下出现的概率是0.001。
图6-2 NB算法结果展示图
K近邻算法
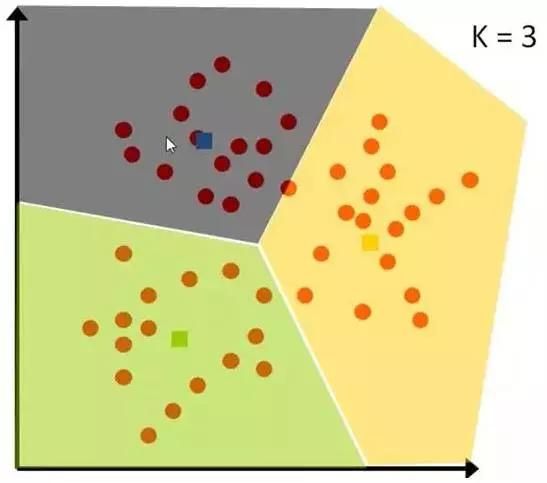
给一个新的数据时,离它最近的 k 个点中,哪个类别多,这个数据就属于哪一类。
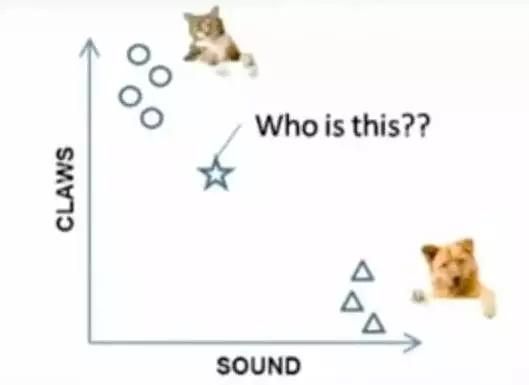
例子:要区分“猫”和“狗”,通过“claws”和“sound”两个feature来判断的话,圆形和三角形是已知分类的了,那么这个“star”代表的是哪一类呢?
图7-1 问题案例
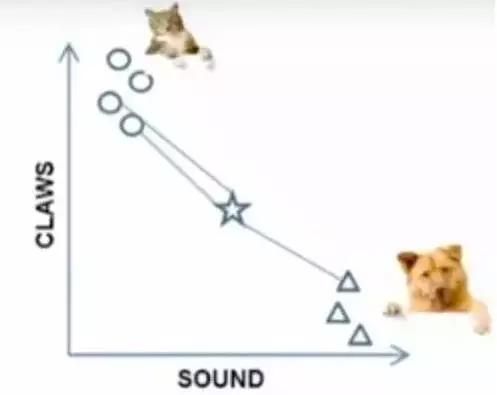
k=3时,这三条线链接的点就是最近的三个点,那么圆形多一些,所以这个star就是属于猫。
图7-2 算法步骤展示图
K均值算法
先要将一组数据,分为三类,粉色数值大,黄色数值小 。最开始先初始化,这里面选了最简单的 3,2,1 作为各类的初始值 。剩下的数据里,每个都与三个初始值计算距离,然后归类到离它最近的初始值所在类别。
图8-1 问题案例
分好类后,计算每一类的平均值,作为新一轮的中心点:
图8-2
几轮之后,分组不再变化了,就可以停止了:
图8-3 算法结果展示
Adaboost
Adaboost 是 Boosting 的方法之一。Boosting就是把若干个分类效果并不好的分类器综合起来考虑,会得到一个效果比较好的分类器。
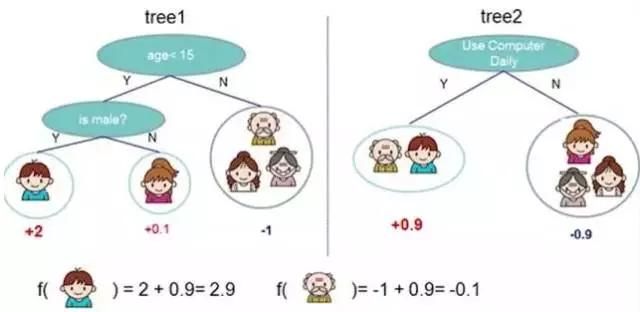
下图,左右两个决策树,单个看是效果不怎么好的,但是把同样的数据投入进去,把两个结果加起来考虑,就会增加可信度。
图9-1 算法原理展示
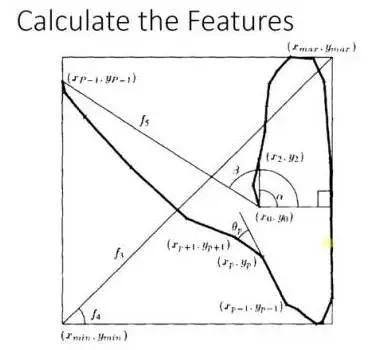
Adaboost 的例子,手写识别中,在画板上可以抓取到很多features(特征),例如始点的方向,始点和终点的距离等等。
图9-2
training的时候,会得到每个feature的weight(权重),例如2和3的开头部分很像,这个feature对分类起到的作用很小,它的权重也就会较小。
图9-3
而这个alpha角就具有很强的识别性,这个feature的权重就会较大,最后的预测结果是综合考虑这些feature的结果。
图9-4
神经网络
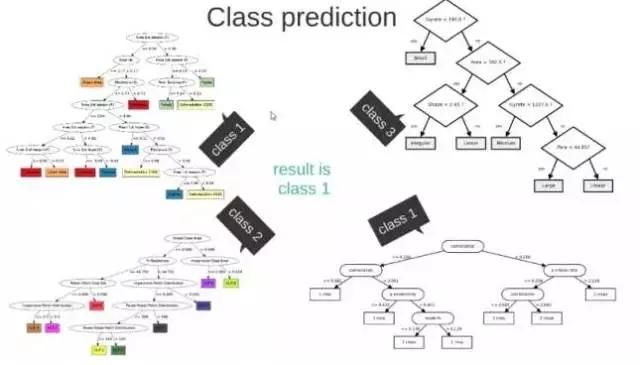
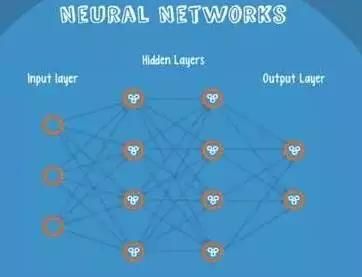
Neural Networks适合一个input可能落入至少两个类别里:NN由若干层神经元,和它们之间的联系组成。 第一层是input层,最后一层是output层。在hidden层和output层都有自己的classifier。
图10-1 神经网络结构
input输入到网络中,被激活,计算的分数被传递到下一层,激活后面的神经层,最后output层的节点上的分数代表属于各类的分数,下图例子得到分类结果为class 1;同样的input被传输到不同的节点上,之所以会得到不同的结果是因为各自节点有不同的weights 和bias,这也就是forward propagation。
图10-2 算法结果展示
马尔科夫
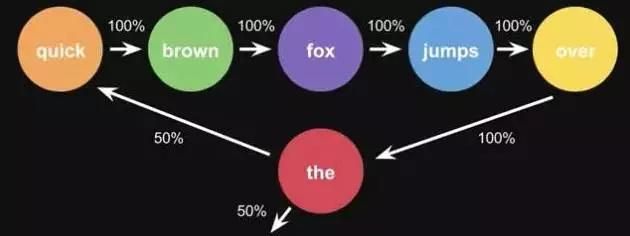
Markov Chains由state(状态)和transitions(转移)组成。例子,根据这一句话 ‘the quick brown fox jumps over the lazy dog’,要得到markov chains。
步骤,先给每一个单词设定成一个状态,然后计算状态间转换的概率。
图11-1 马尔科夫原理图
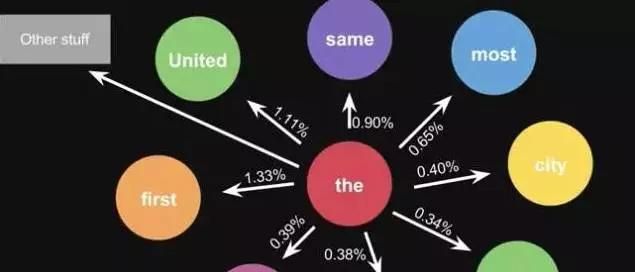
这是一句话计算出来的概率,当你用大量文本去做统计的时候,会得到更大的状态转移矩阵,例如the后面可以连接的单词,及相应的概率。
图11-2 算法结果展示
上述十大类机器学习算法是人工智能发展的践行者,即使在当下,依然在数据挖掘以及小样本的人工智能问题中被广泛使用。