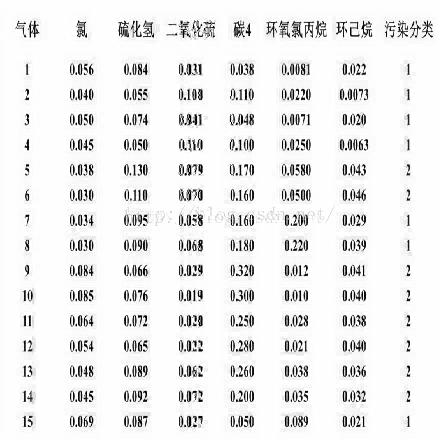
小波融合---超分辨率重建

在《小波图像融合的Matlab实现示例（添加图片演示080428）》一文中，有示例图

1。远景模糊近景清晰的 2。远景清晰近景模糊的3。小波融合

这好象有点超分辨率重建的意思了。

复制了它的代码，缺少一些函数。搜索了一阵，在《小波融合 高频区域能量取大 低频平均 matlab》的文章中找到可以运行的代码

 lowfrefus 函数（低频融合）两者不同，并且一个高频部分没用上 nlfilter 

由于图像太小，没有看出明显差别

下面把《小波融合 高频区域能量取大 低频平均 matlab》的文中的用到的复制过来

%高频区域能量取大，低频平均
function y=imfus(I1,I2)

st=cputime; %程序开始运行时的cpu时间 
 
if(nargin~=2)
    I1=imread('o_Fus01.jpg');
    I2=imread('o_Fus02.jpg');
end
I1=rgb2gray(I1);
I2=rgb2gray(I2);


 [r1,c1]=size(I1);% 读取图像分解后的小波分解系数矩阵的大小

 [r2,c2]=size(I2);
 if(r1~=r2)||(c1~=c2)
     error('图像尺寸不匹配。图像大小必须相同！');
    return;
 end 
 dim=3;%小波分解层数
%  
y1=mywavedec2(I1,dim);

y2=mywavedec2(I2,dim);
%-----------------分解结束，下面 融合--------
% 高频
y11=nlfilter(y1,[3 3],@myfunction3);
y21=nlfilter(y2,[3 3],@myfunction3);
%y11=y1;y21=y2;
[m,n]=size(y11);
for i=1:m
    for j=1:n
        if abs(y11(i,j))>abs(y21(i,j))
            y3(i,j)=y1(i,j);
 
        else
            y3(i,j)=y2(i,j);
 
        end 
    end 
end 
[r,c]=size(y1);% 根据低频融合算法进行图像融合
LLa=y1(1:r/(2^dim),1:c/(2^dim));% 调用lowfrefus函数对低频部分的小波分解系数 进行融合，剩下之前计算得系数，为高频 
LLb=y2(1:r/(2^dim),1:c/(2^dim));
 y3(1:r/(2^dim),1:c/(2^dim))=lowfrefus(LLa,LLb);
 
 y=mywaverec2(y3,dim);% 调用mywaverec2函数重构融合图像 
 y=uint8(y);
 %imwrite(yy,'重构图像.jpg');
 et=cputime-st;

 disp(['用时：',num2str(et)]);

%小波分解
function y1=mywavedec2(I1,dim) 

I1=modmat(I1,dim);% 首先规范化输入矩阵，使其行列数均能被2^dim 整除， 从而使分解顺利进行 
figure;
subplot(121);
imshow(I1);
title('原始图像'); %画出规范化后的源图像

 [m,n]=size(I1);%求出规范化矩阵x的行列数 
 
 xd=double(I1);%将矩阵x的数据格式转换为适合数值处理的double 格式 
 
 for i=1:dim 
     xd=modmat(xd,1);
     [dLL,dHL,dLH,dHH]=mydwt2(xd); %矩阵小波分解
    
     tmp=[dLL,dHL;dLH,dHH];%将分解系数存入缓存矩阵
     
     xd=dLL;    %将缓存矩阵左上角部分的子矩阵作为下一层分解的源矩阵 
 
     [row,col]=size(tmp); %求出缓存矩阵的行列数
    
     y1(1:row,1:col)=tmp;%将缓存矩阵存入输出矩阵的相应行列
     
 end 
 yd=y1;%uint8(y1);%将输出矩阵的数据格式转换为适合显示图像的uint8格式
for i=1:dim %  对矩阵yd 进行分界线处理，画出分解图像的分界线 
    m=m-mod(m,2);
    n=n-mod(n,2);
    yd(m/2,1:n)=255;%0;%
    yd(1:m,n/2)=255;%0;%
    m=m/2;n=n/2;
end
 subplot(122);
imshow(uint8(yd));
title([ num2str(dim) ' 层小波分解图像' ]);

 % 规范化输入矩阵，使其行列数均能被2^dim 整除， 从而使分解顺利进行 
 function y=modmat(x,dim) 
     
 
 [row,col]=size(x);%求出输入矩阵的行列数row,col
 rt=row-mod(row,2^dim); %将row,col分别减去本身模 2^dim 得到的数 
 ct=col-mod(col,2^dim); %所得的差为rt、ct，均能被2^dim 整除 
 

 y=x(1:rt,1:ct); %输出矩阵 y 为输入矩阵 x 的 rt*ct 维子矩阵
 
function [LL,HL,LH,HH]=mydwt2(x)
    
lpd=[1/2 1/2];hpd=[-1/2 1/2];%默认的低通、高通滤波器

[row,col]=size(x);

for j=1:row %首先对输入矩阵的每一行序列进行一维离散小波分解 
    tmp1=x(j,:);
    [ca1,cd1]=mydwt(tmp1,lpd,hpd,1);
    x(j,:)=[ca1,cd1];%将分解系数序列再存入矩阵x中，得到[L|H]
end 
for k=1:col %再对输入矩阵的每一列序列进行一维离散小波分解 
    tmp2=x(:,k);
    [ca2,cd2]=mydwt(tmp2,lpd,hpd,1);
    x(:,k)=[ca2,cd2]; %将分解所得系数存入矩阵 x 中，得到[LL,Hl;LH,HH] 
end 
 
 LL=x(1:row/2,1:col/2);%LL是矩阵x 的左上角部分 
 
 
 LH=x(row/2+1:row,1:col/2); %LH是矩阵x 的左下角部分 

 
 HL=x(1:row/2,col/2+1:col);%HL是矩阵x 的右上角部分 
 
 
 HH=x(row/2+1:row,col/2+1:col);%HH是矩阵x 的右下角部分 
 
 
function [cA,cD]= mydwt(x,lpd,hpd,dim)
cA=x;%初始化cA
cD=[];
for i=1:dim
    cvl=conv(cA,lpd); %低通滤波，为了提高运行速度，调用MATLAB 提供的卷积函数 conv() 
    dnl=downspl(cvl); %通过下抽样求出平均部分的分解系数
    cvh=conv(cA,hpd); %高通滤波
    dnh=downspl(cvh); %通过下抽样求出本层分解后的细节部分系数
    cA=dnl; %下抽样后的平均部分系数进入下一层分解
    cD=[cD,dnh];%将本层分解所得的细节部分系数存入序列cD
end 

 %下采样
 function y=downspl(x);
 N=length(x);% 读取输入序列长度
 M=floor(N/2);%输出序列的长度是输入序列长度的一半（带小数时取整数部分）
 i=1:M;
 y(i)=x(2*i);

%求滑动窗口中的元素的平方和
function c=myfunction3(x)

y=0;
%平方和
% for i=1:numel(x)
%    y=x(i).^2+y;
% end
%差值和
for i=2:numel(x)
    y=abs(x(i-1)-x(i))+y;
end
c=y;

%小波重构
 function y=mywaverec2(x,dim) 
 
 xd=uint8(x);% 将输入矩阵的数据格式转换为适合显示图像的uint8格式 
 [m,n]=size(x);
 for i=1:dim %对转换矩阵xd进行分界线处理 
     m=m-mod(m,2);
     n=n-mod(n,2);
     xd(m/2,1:n)=255;%0;%
     xd(1:m,n/2)=255;%0;%
     m=m/2;n=n/2;
 end
figure;
 subplot(121);imshow(xd);
title([ num2str(dim) ' 层小波分解图像']);%画出带有分界线的分解图像 
xr=double(x);% 将输入矩阵的数据格式转换回适合数值处理的double格式 
[row,col]=size(xr);% 求出转换矩阵xr的行列数 
for i=dim:-1:1 %重构次序是从内层往外层进行，所以先抽取矩阵xr 的最内层 分解矩阵进行重构 
    tmp=xr(1:floor(row/2^(i-1)),1:floor(col/2^(i-1)));% 重构的内层矩阵的行列数均为矩阵xr 的2^(i-1) 
    [rt1,ct1]=size(tmp);% 读取待重构矩阵tmp 的行列数 
    rt=rt1-mod(rt1,2);ct=ct1-mod(ct1,2);
     rLL=tmp(1:rt/2,1:ct/2);% 将待重构矩阵tmp 分解为四个部分 
     rHL=tmp(1:rt/2,ct/2+1:ct);
     rLH=tmp(rt/2+1:rt,1:ct/2);
     rHH=tmp(rt/2+1:rt,ct/2+1:ct);
     tmp(1:rt,1:ct)=myidwt2(rLL,rHL,rLH,rHH);% 将重构结果返回到矩阵tmp 
     xr(1:rt1,1:ct1)=tmp;% 把矩阵tmp 的数据返回到矩阵 xr 的相应区域，准备 下一个外层的重构 
end 
y=xr;% 重构结束后得到的矩阵xr即为输出矩阵y 
yu=uint8(xr);%将矩阵xr的数据格式转换为适合显示图像的uint8 格式 
subplot(122);
imshow(yu);
title('小波重构融合图像');

function y=myidwt2(LL,HL,LH,HH);

 lpr=[1 1];hpr=[1 -1];% 默认的低通、高通滤波器
 tmp_mat=[LL,HL;LH,HH];% 将输入的四个矩阵组合为一个矩阵
 [row,col]=size(tmp_mat);
 
for k= 1:col %首先对组合矩阵tmp_mat的每一列，分开成上下两半 
    ca1=tmp_mat(1:row/2,k);% 分开的两部分分别作为平均系数序列ca1、细节系数 序列cd1 
    cd1=tmp_mat(row/2+1:row,k);
    tmp1=myidwt(ca1,cd1,lpr,hpr);% 重构序列
    yt(:,k)=tmp1;% 将重构序列存入待输出矩阵yt 的相应列，此时 y=[L|H]
end
for j=1:row %将输出矩阵 y 的每一行，分开成左右两半
    ca2=yt(j,1:col/2);% 分开的两部分分别作为平均系数序列ca2、细节系数序列cd2 
    cd2=yt(j,col/2+1:col);
    tmp2=myidwt(ca2,cd2,lpr,hpr);% 重构序列
    yt(j,:)=tmp2;% 将重构序列存入待输出矩阵yt 的相应行，得到最终 的输出矩阵 y=yt 
end 
y=yt;

function y=myidwt(cA,cD,lpr,hpr);

lca=length(cA);% 求出平均、细节部分分解系数的长度
lcd=length(cD);

 while (lcd)>=(lca) % 每一层重构中，cA 和 cD 的长度要相等，故每层重构后， 
                    % lcd小于 lca，则重构停止，这时的 cA 即为重构信号 序列 y 。 
      upl=upspl(cA);%对平均部分系数进行上抽样
      cvl=conv(upl,lpr);% 低通卷积
      cD_up=cD(lcd-lca+1:lcd);% 取出本层重构所需的细节部分系数，长度与本层平均部分系数的长度相等 
      uph=upspl(cD_up);% 对细节部分系数进行上抽样
      cvh=conv(uph,hpr);% 高通卷积
      cA=cvl+cvh;% 用本层重构的序列更新cA，以进行下一层重构
      cD=cD(1:lcd-lca);% 舍弃本层重构用到的细节部分系数，更新cD
      lca=length(cA);% 求出下一层重构所用的平均、细节部分系数的长度
      lcd=length(cD);
 end %lcd

如果还要用到其它函数，自行去复制吧

如果要比较两者不同效果，也自行去复制lowfrefus 相关吧。

=====================================

又在《matlab使用小波变换进行图像融合》一文中找到两个示例图

12

运行该文中的小波融合：

中间哪个水印好象消失了

运行本文的小波融合：

水印又出来了，一个只有平均，一个加了高频取大，效果就是不一样。