模拟用户弧线滑动，算法python实现

前言

用自动化软件执行脚本时，其中拖拽、滑动等这些操作往往是直线，而实际用户滑动时一般都不是直线，可能是一段弧线或者更复杂的线。

下面就介绍一种计算两个点直线弧线路径的方法，并通过 python 和 sikuli 实现弧线滑动

弧线坐标计算

已知 A、B两点坐标分别为(x1,y1)、（x2,y2），求经过A、B两点的弧线，显然这样的弧线有无数条，需要再加上限定条件，弧线的弧度φ，也就是A、B两点和圆心连线的夹角，范围是(0, π)，限定弧度后，这样的弧线就只剩两条了。

1. 求出圆心坐标

如图，先考虑B在A右上方，弧线位于AB下方的情况：

一开始想用圆心坐标列二元二次方程组，比较麻烦，就改用三角函数来运算，效果很好。主要思路就是求出其中一条半径 OA的长度和斜率，再通过 A 点坐标增量的方式求出圆心 O 的坐标

AB的长度 d = ((x2-x1)^2 + (y2-y1)^2) ^(1/2)
OA与AB的夹角 α= (π - φ)/2
根据正弦定理求半径 r = d/sinα* sinφ
AB与x轴的夹角 β= arctan((y2-y1)/(x2-x1))
OA与x轴的夹角 γ=α+β
最后O点坐标为 (x0, y0) = (x1+r*cosinγ, y1+r*sinγ)

其他情况处理：
图中各条线的相对位置只是一种情况，其他情况计算公式可能稍有不同，某些地方的加减号可能要互换。经过验证，只要把求β的步骤中的arctan(a)换成一个二元函数atan2(x,y)就可以适应各种情况了。
具体就是 β= atan2((y2-y1),(x2-x1))
atan2和arctan的不同之处是，arctan返回的是一个180°的范围(-π/2, π/2)的值，而atan2(x, y)则会根据x, y值是正数还是负数，也可以理解成点(x, y)所在的象限，返回一个360°范围(-π, π)的角度值，并且这个角度的正切值是 y/x 。
具体验证过程就不写了，atan2函数在python的math包里有，后面代码部分会介绍。

2. 求出弧线上采样点的坐标

知道了圆心(x0,y0)和半径r，可以求出圆上任意一点的坐标。但是我们要的是画出A点到B点之间的一段弧线。而让软件画出这段弧线，其实就是要在某种索引下，将鼠标或者模拟手指（触屏设备），依次划过这段弧线上离散采样的n个点。

那这个索引选什么比较好呢，首先想到坐标x,y中的一个作为索引，但这样是不行的，因为单一一个横坐标或者纵坐标与点不是一一对应的，给出一个x，求圆上的点有可能求出两个y

索引可以选择点所在的半径和x轴的夹角，夹角与圆上的点一一对应的，用atan2（x,y）函数也能很容易的求出夹角来。

首先要有已知圆上点坐标求夹角的公式，这样才能分别求出起始和结束点的夹角，已确定夹角作为索引时的其实和结束范围

圆上点(x,y)的夹角α = atan2(x-x0, y-y0)
那么起始点A的夹角 α1 = atan2(x1-x0, y1-y0)
结束点B的夹角 α2 = atan2(x2-x0, y2-y0)

已知夹角求圆上点的坐标，因为sin和cos都是周期为2π的，所以这里夹角的取值范围不需要限制在(-π,π )之间，可以是任意值：

x = x0 + r*cosα
y = y0 + r*sinα

确定索引范围
知道起始和结束的夹角，如果需要采样n个点，把起始和结束点之间分割成n个角度，再求出对应点的坐标，不就可以了吗？有时可能没那么简单，之前还需要加一步，夹角范围翻转，如图：

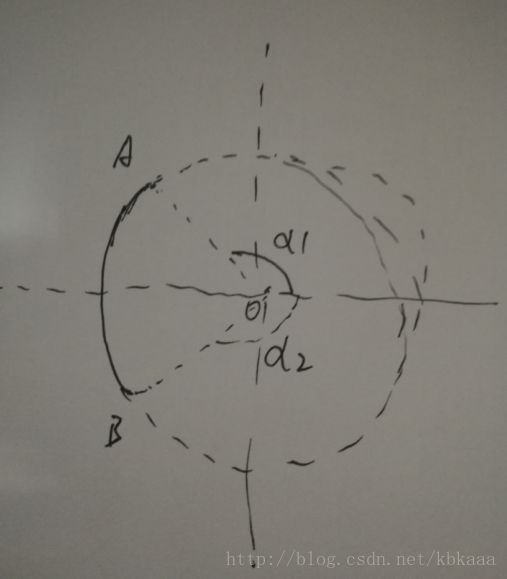
当AB之间夹角跨度超过180°时，虽然我们想要的是实线部分较短的这一段弧线，但直接用α1和α2的话，得到的会是虚线部分，较长的这一段弧线。因此要首先进行判断，如果α1减α2的绝对值大于π，则需要将其中较小的一个加上2π，这样才能得到较短的那段弧线

代码实现

这里使用python和sikuliX，sikuliX(http://www.sikulix.com/)是一款基于计算机视觉的自动化工具。

from __future__ import division
import random
import math

def distance(location1, location2):
    return math.sqrt((location1.getX() - location2.getX())**2 + (location1.getY() - location2.getY())**2)

def getCircleXY(a, x0, y0, r):
    x = x0 + r * math.cos(a)
    y = y0 + r * math.sin(a)
    return (x,y)

def getAngleXY(x, y, x0, y0):
    return math.atan2(y-y0, x-x0)

def getAngle(location1, location0):
    return getAngleXY(location1.getX(), location1.getY(), location0.getX(), location0.getY())

def dragDropX(location1, location2, dragTime):
    print "[Debug]start dragDropX function"
    x1 = location1.getX()
    y1 = location1.getY()
    x2 = location2.getX()
    y2 = location2.getY()
    connerA = math.pi / 6
    connerB = (math.pi - connerA)/2
    d0 = math.sqrt((x2-x1)**2 + (y2-y1)**2)
    r = d0 * math.sin(connerB)/math.sin(connerA)
    connerC = math.atan2((y2-y1),(x2-x1))
    connerD = connerC + connerB

    x0 = x1 + r * math.cos(connerD)
    y0 = y1 + r * math.sin(connerD)
    location0 = Location(x0, y0)

    startPoint = location1
    endPoint = location2
    startAngle = getAngle(startPoint, location0)
    endAngle = getAngle(endPoint, location0)
    if abs(endAngle - startAngle) > math.pi:
        if endAngle < startAngle:
            endAngle += math.pi * 2
        else:
            startAngle += math.pi * 2

    n = 30
    jitter = math.ceil(r * abs(endAngle - startAngle)/n/10)
    mmd = Settings.MoveMouseDelay
    threadLock.acquire()
    mouseMove(startPoint)
    mouseDown(Button.LEFT)
    Settings.MoveMouseDelay = dragTime/n  
    angleStep = (endAngle - startAngle) / n
    for i in range(n):
        angle = startAngle + angleStep * i
        lo = getCircleXY(angle, x0, y0, r)
        mouseMove(Location(lo[0]+random.randint(-jitter,jitter), lo[1]+random.randint(-jitter,jitter)))
    mouseMove(endPoint)
    mouseUp(Button.LEFT)
    threadLock.release()
    Settings.MoveMouseDelay = mmd

实现效果

利用sikuliX编辑脚本，在屏幕上查找两个形状，再从一个执行弧形滑动到另一个形状。

下面为效果图，不同颜色对应不同的弧度值，分别是60°、30°、15°、7.5°