DeepLabv1补充:对全连接条件随机场(Fully Connected / Dense CRF)的理解
1. 随机场 (random field)
由若干位置组成的整体,每一个位置按某种分布随机地赋一个值,全体即组成一个随机场。
2. 马尔科夫随机场(MRF)
马尔科夫随机场是随机场的特例,假设某一个位置的赋值只与和它相邻的位置相关。
3. 条件随机场(CRF)
条件随机场是马尔科夫随机场的特例,假设马尔可夫随机场只有X和Y两个随机变量,一般情况下,X是给定的,Y是输出。
形式化定义:设X和Y是随机变量, P ( Y ∣ X ) P(Y|X) P(Y∣X)是给定X时Y的条件概率分布,若Y构成一个马尔科夫随机场,则 P ( Y ∣ X ) P(Y|X) P(Y∣X)是条件随机场。
4. 线性链条件随机场(linear CRF)
若X和Y有相同的结构,即 X = ( X 1 , X 2 , . . . , X n ) , Y = ( Y 1 , Y 2 , . . . Y n ) X=(X_1,X_2,...,X_n),Y=(Y_1,Y_2,...Y_n) X=(X1,X2,...,Xn),Y=(Y1,Y2,...Yn),则构成线性链(linear chain)条件随机场。
形式化定义:设 X = ( X 1 , X 2 , . . . , X n ) , Y = ( Y 1 , Y 2 , . . . Y n ) X=(X_1,X_2,...,X_n),Y=(Y_1,Y_2,...Y_n) X=(X1,X2,...,Xn),Y=(Y1,Y2,...Yn)均为线性链表示的随机变量序列,在给定随机变量序列X的情况下,如果随机变量Y的条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)构成条件随机场,即具有马尔科夫性,即:
P ( Y i ∣ X , Y 1 , Y 2 , . . . , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) P(Y_i|X,Y_1,Y_2,...,Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1}) P(Yi∣X,Y1,Y2,...,Yn)=P(Yi∣X,Yi−1,Yi+1)
则$P(Y|X)是线性链条件随机场
5. 全连接条件随机场(Fully Connected / Dense CRF)
如下图,有一幅图像:
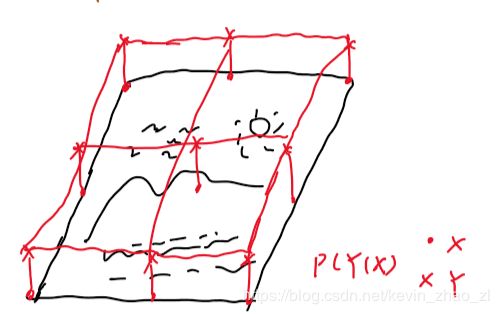
若像素类别之和自己所在的像素点有关,则建模如下图:

更加复杂地,每一个像素类别和图像中所有像素有关,则如下图:
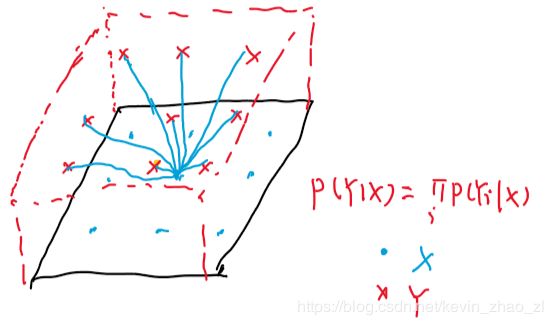
更加fancy的,每一个像素类别和它的一个4邻域相关,如下图所示:
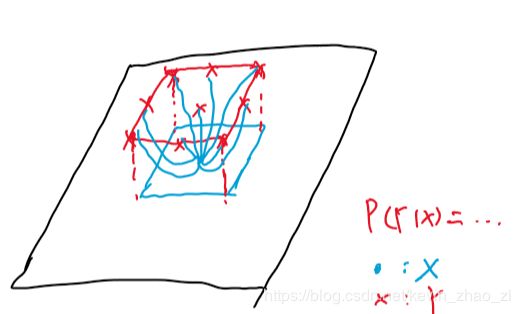
最复杂的,把能连的都连起来,构成全连接CRF,即Dense CRF。下图并没有画全所有连接:
