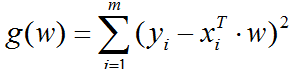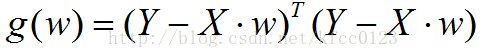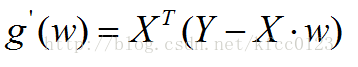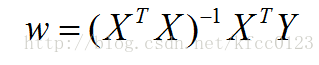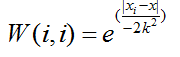线性回归算法及用python实现
一、线性回归算法简介
1、线性回归:
线性回归是利用数理统计中的回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。在线性回归中,数据使用线性预测函数来建模,并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。
回归的目的就是预测数值型的目标值,因此我们要用线性回归找到一条最佳拟合直线。
2、回归系数的求解:
设最佳拟合直线为:y(x)=w^T*x,其中回归系数w=(w0,w1,w2,...,wn),变量x=(1,x1,x2,...,xn),w^T表示w的转置
对于任意一个数据(x(i),y(i)),与最佳拟合直线的误差为:|y(x(i))-y(i)|=|w^T*x(i)-y(i)|
在这里我们用最小二乘法算误差,即:(w^T*x(i)-y(i))^2
而y(x)为最佳拟合直线,意味着所有的点的误差最小。即:
而我们要做就是使所有误差最小的回归参数w
用矩阵可以这样表示:
对w求导,得:
令上式等于0,得:
即:
3、局部加权线性回归:
线性回归有一个问题就是欠拟合,解决这个问题方法就是局部加权线性回归。
我们给预测点附近的每个点都赋予一定的权重,得到的回归系数为:
其中:W为矩阵,除对角线外其他元素均为0
二、python代码的实现
在实现代码前,你需要先建立一个含有数据点的文本,比如ex0.txt,文本格式为:
当然,你也可以代入自己的数据点
1、线性回归:
from numpy import *
import matplotlib.pyplot as plt
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1 #得到特征值的个数
dataMat = []; labelMat = []
fr = open(fileName) #打开文件
for line in fr.readlines(): #读取整行
lineArr =[]
curLine = line.strip().split('\t') #将一行的不同特征分开
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def standRegres(xArr,yArr):
xMat = mat(xArr); yMat = mat(yArr).T
xTx = xMat.T*xMat
ws = xTx.I * (xMat.T*yMat) #求 w=(x.T*x).I*x.T*y
return ws
a,b=loadDataSet('ex0.txt')
ws=standRegres(a,b)
print ws
x=arange(0,1,0.01)
plt.plot([i[1] for i in a],b,'or')
plt.plot(x,float(ws[0])+float(ws[1])*x,'g')
plt.show()[[ 3.00772239]
[ 1.66874279]]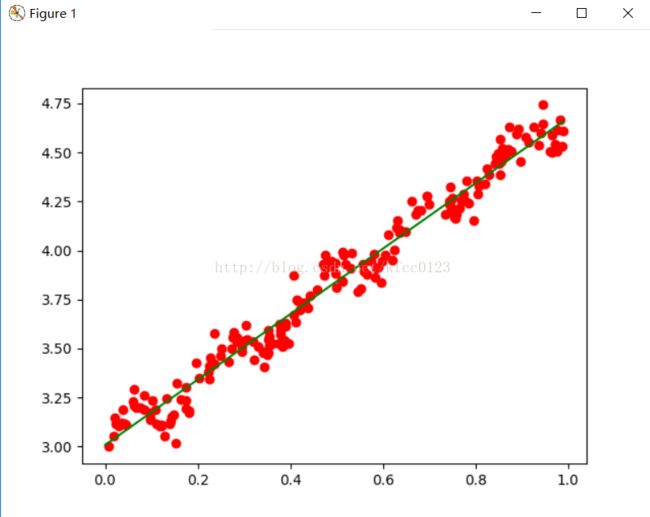
局部加权线性回归
from numpy import *
import matplotlib.pyplot as plt
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1 #得到特征值的个数
dataMat = []; labelMat = []
fr = open(fileName) #打开文件
for line in fr.readlines(): #读取整行
lineArr =[]
curLine = line.strip().split('\t') #将一行的不同特征分开
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def lwlr(testPoint,xArr,yArr,k=1.0):
xMat = mat(xArr); yMat = mat(yArr).T
m = shape(xMat)[0] #m为行数
weights = mat(eye((m))) #创建m*m的单位矩阵
for j in range(m):
diffMat = testPoint - xMat[j,:]
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) #对角线上的元素改为exp(|x(i)-x|/(-2k*k))
xTx = xMat.T * (weights * xMat)
ws= xTx.I * (xMat.T * (weights * yMat)) #求 w=(x.T*W*x).I*x.T*W*y
return testPoint * ws
def lwlrTestPlot(xArr,yArr,k=1.0):
y = zeros(shape(yArr))
Arr=[i[1] for i in xArr]
xCopy = mat(xArr);x=mat(Arr).T #将列表转化为矩阵
xCopy.sort(0);x.sort(0) #给矩阵从小到大排序
for i in range(shape(xArr)[0]):
y[i] = lwlr(xCopy[i],xArr,yArr,k) #调用lwlr函数
return x,y
a,b=loadDataSet('ex0.txt')
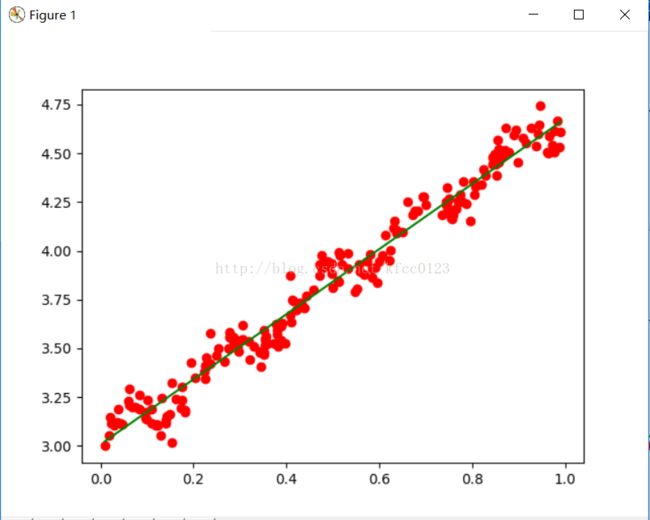
plt.figure(1)
c,d=lwlrTestPlot(a,b,1)
plt.plot([i[1] for i in a],b,'or')
plt.plot(c,d,'g')
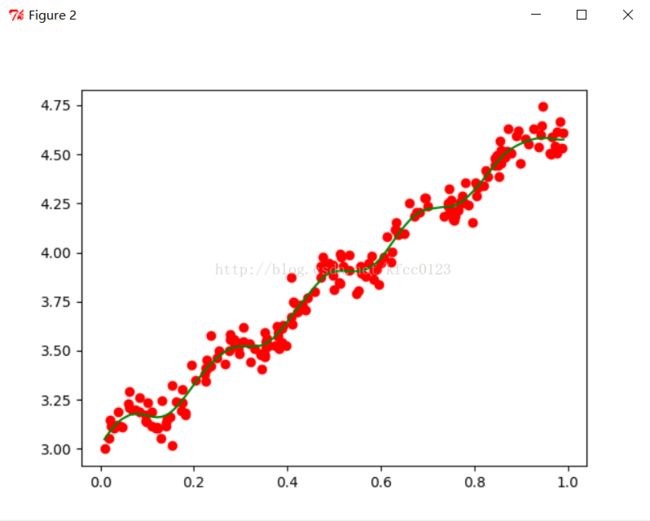
plt.figure(2)
c,d=lwlrTestPlot(a,b,0.03)
plt.plot([i[1] for i in a],b,'or')
plt.plot(c,d,'g')
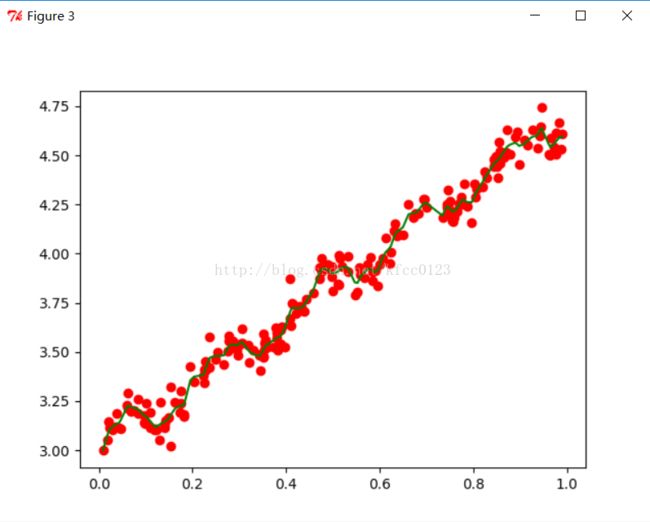
plt.figure(3)
c,d=lwlrTestPlot(a,b,0.008)
plt.plot([i[1] for i in a],b,'or')
plt.plot(c,d,'g')
plt.show()很明显:当k=1时,就是线性回归图像,存在欠拟合现象;
当k=0.03时,效果比较好;
当k=0.008时,存在过拟合现象