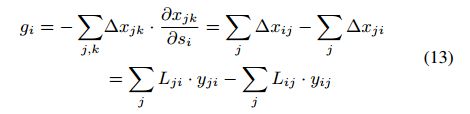感知算法论文(九):Towards Accurate One-Stage Object Detection with AP-Loss
文章目录
- 摘要
- 1. 引言
- 2. 相关工作
- 3. 方法
- 3.1 Ranking Task 和 AP-loss
- 3.1.1 Ranking Task
- 3.1.2 AP-loss
- 3.2 最优化准则
- 3.2.1 误差驱动更新
- 3.2.2 反向传播
- 3.3 分析
- 3.4 训练方法的细节
- 4. 实验
- 4.1 实验设置
- 4.2 消融学习
- 4.2.1 不同参数的对比
- 4.2.2 不同 loss 的对比
- 4.2.3 不同优化方法的对比
- 4.3 基准结果
- 5. 结论
摘要
单阶段目标检测器是通过同时优化分类损失和定位损失来训练的
由于anchor的数量很多,存在前景目标和背景目标不平衡的问题
本文提出了一种新的框架来缓和上述不平衡问题,即使用排序方法来代替分类任务,并且使用 Average-Precision loss(AP-loss)来完成排序问题。
因为 AP-loss 是不可微且非凸的,AP-loss 不能直接被优化,故本文使用一种新的优化方法,可以将感知学习过程的误差驱动的更新机制和深度网络中的反向传播机制进行巧妙的结合。
1. 引言
目标检测需要从背景中定位并识别出目标,其面临的挑战是前景和背景数量极不平衡。
检测过程是一个多任务机制,需要用不同的损失函数来解决分类任务和定位任务。
分类任务主要是识别b-box中的目标的类别,定位任务主要是预测b-box的位置。
两阶段的检测器,首先生成确定数量的候选框,所有检测问题可以从这些候选框中直接解决。
单阶段的检测器,需要直接从大量的预定义的候选框中预测目标类别,大量的b-box会引起前景和背景的极度不平衡,使得分类任务难以进行。
已知,对于一个平凡解(无解),几乎所有的候选框都被预测为负标签,分类指标可能很高,而检测性能较差。如图1(a)所示。

为了解决单阶段目标检测的这种问题,很多不同的方法引入了新的分类损失,如 balanced loss[23]、Focal loss[15] 和 tailored training 方法(Online Hard Example Mining (OHEM))等。这些 losses 对每个 anchor box 都分别独立建模,在分类损失中,其尝试对前景样本和背景样本重新赋权值,来适应样本不平衡的情况,这些方法没有考虑不同 samples 之间的联系。设计的平衡权重是手工选取的超参数,并不能很好的适应于不同类型的数据集。
本文认为,分类任务和检测任务之间的鸿沟阻碍了单阶段目标检测器的性能提升,本文并未从分类损失函数的修正上着手,而是直接使用排序方法(ranking)来代替分类损失。其中,关联的 ranking loss 显式地对关系建模,并且对正样本和负样本的比例不敏感。
如图1(b)所示,本文使用 AP 作为本文目标损失,其本质上更符合目标检测的评价指标。
由于 AP- loss 是不可微且非凸的,所以标准的梯度下降方法无法训练,下面讨论三点:
1)在结构化的 SVM 模型中学习了基于 AP 的 loss,该 SVM 模型是线性模型,所以性能受限。
2)结构化的 hinge loss 用于优化 AP loss的上届,而不是直接优化 loss 本身
3)近似的梯度方法可以用于优化 AP-loss,但效率不高,且容易陷入局部最优。
综上,优化 AP-loss 仍然是一个开放性问题。
本文中,我们用 ranking task 来代替单阶段检测器的 classification task,故我们使用基于 ranking 的 loss(AP-loss)来解决类别不平衡的问题。
详细来讲,本文提出了一种新的基于误差的学习策略,来有效的优化基于 AP 的不可微的目标检测函数。
也就是说,给单阶段检测器的得分输出添加了一些额外的变换,来获得 AP- loss,包括线性变换(将 scores 变换成成对的偏差),之后利用非线性且不可微的“激活函数”将成对偏差变换成 AP-loss 的主要内容,最后就可以通过将原始 term 和 label vector 进行点乘来获得 AP-loss。
受感知学习方法的启发,我们使用误差驱动的学习方式,来直接通过不可微的激活函数传递更新的信号。
不同于梯度方法,我们的学习机制给每个变量的误差一个更新信号的比率,之后使用反向传播来传递权值更新信号。
本文从理论和实际上都证明了提出的优化方法不会出现不可微可非凸的情况,本文主要贡献如下:
- 提出了新的框架来解决分类样本正负不均衡的问题
- 提出了误差驱动的学习机制,可以有效地优化不可微且非凸的基于 AP 的目标函数
- 通过实验验证,本文方法相比于使用 classification loss 的方法效果更好
2. 相关工作
单阶段检测器:目标检测中,单阶段方法可以比两阶段方法更简单且更高效。
众所周知,单阶段目标检测器的优良效果得益于密集的anchors,但这会导致前景和背景目标的不平衡,为了解决这个问题,OHEM [18, 31] 和 Focal Loss [15] 被用来降低简单样本的权重,然而,该问题仍然没有得到有效的解决。
首先,手选超参数难以泛化到其他数据集
其次,anchors 之间的关系没有很好的建模
用于目标检测的 AP loss:
AP 被当做评价指标,但由于其不可微和非凸性,难以用作优化函数,本文的方法有四个特点:
1)本文方法可以被用于任何可微线性或可微非线性模型,如神经网络,其他的那些方法,如[37,19] 仅仅可以在线性 SVM 模型中起作用。
2)本文方法直接优化 AP- loss,[20]会导致 loss 出现 gap
3)本文方法不是近似的梯度,且不受 [34,9] 中的目标函数非凸性的影响
4)本文方法可以端到端的训练检测器
感知学习方法:
本文优化准则的核心是“误差驱动更新”,是感知学习方法的泛化版本,有助于克服不可微目标函数的困难。
感知器是使用阶跃函数作为激活函数的简单的人工神经元,感知学习方法是由Frank Rosenblatt [26]最初提出的,因为阶跃函数是不可微的,其不适合于使用梯度更新准则,但该方法也没有使用类似于交叉熵损失函数的方法来代替优化函数,而是使用“误差驱动更新”方法来更新权值。
当训练数据是线性可分的时,该方法能够保证在有限次数内收敛。
3. 方法
我们主要是使用基于 ranking task 的 AP-loss 来代替 classification task。
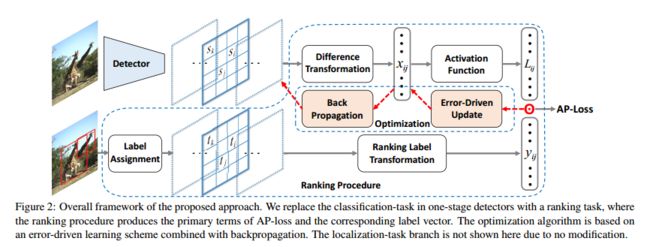
图2展示了本文方法的两个主要结构:ranking 过程 + 误差驱动更新准则
3.1 Ranking Task 和 AP-loss
3.1.1 Ranking Task
传统单阶段检测器:
给定输入图像 I I I
假设预定义的 anchors 序列是 B B B
每个anchor b i ∈ B b_i \in B bi∈B
同时给每个 anchor 根据真实值和 IoU 策略都分配一个 label t i ∈ { − 1 , 0 , 1 , . . . , K } t_i \in \{-1,0,1,...,K \} ti∈{−1,0,1,...,K},1~K 表示目标类别 ID,“0” 表示背景,“-1” 表示忽略的 anchor。
训练和测试阶段,检测器给每个 anchor 都输出一个得分向量 ( s i 0 , . . . , s i K ) (s_i^0, ...,s_i^K) (si0,...,siK)
本框架中,一个 anchor 不再有 K + 1 K+1 K+1 维的得分预测,将每个 anchor 都复制 K 次来得到 b i k b_{ik} bik ,其中 k = 1 , . . . , K k=1,...,K k=1,...,K,且第 k k k 个anchor 负责第 k k k 个类别的检测。
每个 anchor b i k b_{ik} bik 都会依据 IoU 准则(-1 表示未被计入 ranking loss)都会被分配一个 label t i k ∈ { − 1 , 0 , 1 } t_{ik}\in\{-1,0,1\} tik∈{−1,0,1}。
因此,在训练和测试阶段,对于每个 anchor,检测器将仅仅预测一个标量得分 s i k s_{ik} sik。
图3展示了本文的标签分配方法
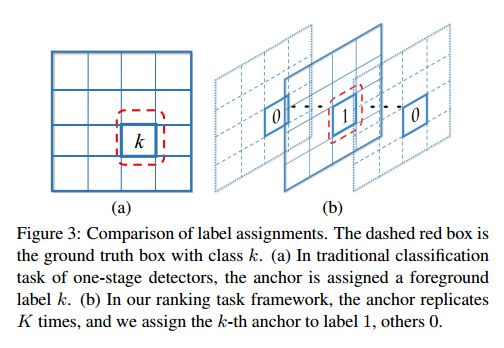
ranking task 影响,每个正值 anchor 都应该被排到负值 anchor 的前面。
ranking 结果的 AP 是从所有类别的得分中得到的,不同于目标检测系统的 meanAP。
我们用这种方法计算 AP,因为得分的分布对所有的类别都是一致的,但对每个类别分别排序的话无法达到这个目标。
3.1.2 AP-loss
为了简单起见,在复制之后我们仍然使用 B B B 来表示 anchor, b i b_i bi 表示第 i i i 个没有复制的 anchor 。
每个 b i b_i bi 对应一个标量得分 s i s_i si 和一个二值label t i t_i ti。
一些变化需要表示为如图2所示的形式。
首先,差分变换将得分 s i s_i si 转化成不同的形式:
![]()
其中, s ( b i ; θ ) s(b_i;\theta) s(bi;θ) 是基于 CNN 的得分函数, θ \theta θ 是 b i b_i bi 的权重。
ranking label 变换将labels t i t_i ti 转化成对应的有序形式::
![]()
其中,1 是指示函数,当满足下标条件时,成立,其他情况都为0。
之后,定义一个向量值激活函数 L ( ⋅ ) L(\cdot) L(⋅) 来得到 AP-loss 的初级形式:
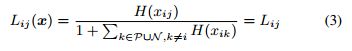
其中, H ( ⋅ ) H(\cdot) H(⋅)是阶跃函数:

当没有两个样本的得分相等时,将该排序定义为 “proper ranking"。
![]()
不失一般性,我们将直接打破该联系,把所有的 ranking 当做 proper ranking 。
此时, AP-loss L A P L_{AP} LAP 变为下列形式:
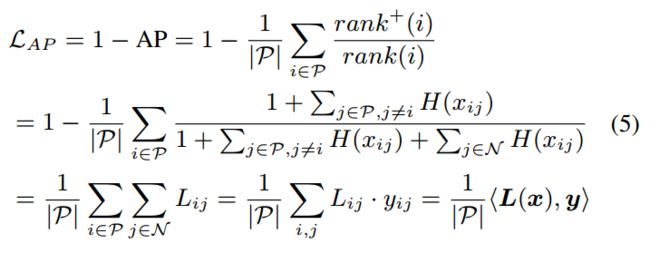
rank(i) 和 rank+(i) 定义了得分 s i s_i si 的ranking 位置
P = { i ∣ t i = 1 } P=\{i|t_i=1\} P={i∣ti=1}, N = { i ∣ t i = 0 } N=\{i|t_i=0\} N={i∣ti=0}, ∣ P ∣ |P| ∣P∣ 是序列 P P P 的大小, L L L 和 y y y 是 L i j L_{ij} Lij 和 y i j y_{ij} yij 的向量形式, < , > <,> <,> 表示内积。
最终,待优化的目标函数为:
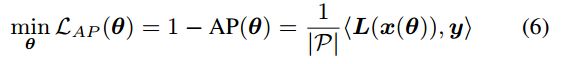
其中, θ \theta θ 是权值,激活函数 L ( ⋅ ) L(\cdot) L(⋅) 是不可微的,故需要一种新的参数更新方法,而非传统的梯度下降法。
除了 AP 指标,其他的基于 ranking 的方法也可以被用来设计 ranking loss。
一个例子是 AUC-loss[12],使用 ROC 曲线下的面积来进行 ranking,且激活函数有些许的特殊:
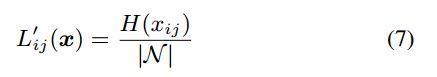
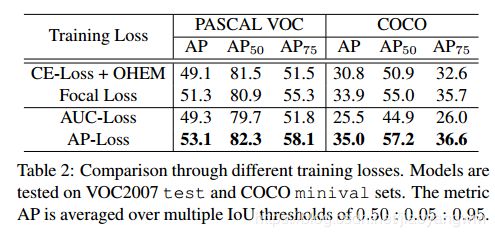
由于 AP 和目标检测任务的评估准则一致的,所以我们认为 AP-loss 直观上比 AUC-loss 更适合于检测任务,并将为我们的实验提供实证研究。
3.2 最优化准则
3.2.1 误差驱动更新
考虑感知学习准则,输入变量的更新方法是“误差驱动”的,也就是说更新是源于期望输出和现有输出的差值。
我们使用该方法,并将其扩展到更一般化的情况,即激活函数的输入和输出是向量。
假设 x i j x_{ij} xij 是输入, L i j L_{ij} Lij 是输出,则 x i j x_{ij} xij 的更新方式如下:
△ x i j = L i j ∗ − L i j \bigtriangleup x_{ij}=L_{ij}^*-L_{ij} △xij=Lij∗−Lij
其中, L i j ∗ L_{ij}^* Lij∗ 是真实标签。
注意到, 当每个项 L i j ⋅ y i j = 0 L_{ij} \cdot y_{ij} =0 Lij⋅yij=0 时,AP-loss 取最小值,且最小值为0。
此时有两种情况:
- 当 y i j = 1 y_{ij}=1 yij=1 时,可以设定期望标签 L i j ∗ = 0 L_{ij}^* =0 Lij∗=0
- 当 y i j = 0 y_{ij}=0 yij=0 时,不关心更新量,且设置其为0,因为此时不会对 AP- loss 有任何贡献。
因此,更新机制简化为:
△ x i j = − L i j ⋅ y i j \bigtriangleup x_{ij}=-L_{ij} \cdot y_{ij} △xij=−Lij⋅yij
3.2.2 反向传播
此时我们有期望更新: △ x \bigtriangleup x △x
之后,需要寻找模型权重 △ θ \bigtriangleup \theta △θ 的更新方式
我们使用点乘来测量连续移动的大小,且用基于 L 2 − n o r m L_2-norm L2−norm 的惩罚方法来调整权重变化( △ θ \bigtriangleup \theta △θ)。
优化问题如下:
![]()
其中, θ ( n ) \theta^{(n)} θ(n) 定义了第 n n n step 的模型权重,第一阶的扩张是:

其中, ∂ x ( θ ( n ) ) / ∂ θ \partial x(\theta^{(n)})/ \partial \theta ∂x(θ(n))/∂θ 是 Jacobian 矩阵。
忽略高阶无穷小,可以得到 step-wise 最小化过程:
之后,最优 △ θ \bigtriangleup \theta △θ 的形式是和链式导数更新法则一致的,这就意味着可以直接将 x i j x_{ij} xij 的梯度设置为 − △ x i j -\bigtriangleup x_{ij} −△xij(Eq.9),且可以通过反向传播进行传递。
所以得分 s i s_i si 的梯度可以通过反向传播差值来获得:
3.3 分析
收敛性:
为了更好的理解 AP- loss 的形状,首先提供了最优准则收敛性的理论分析,其受启发于原始的感知学习方法。
命题1:
在满足以下条件的情况下,能够保证AP- loss 优化准则在有限次内收敛:
1)学习模型是线性的
2)训练数据是线性可分的
一致性:
除了收敛性以外,我们也观察了本文提出的优化准则和 classification-loss 具有内在一致性。
观察1:
当激活函数 L ( ⋅ ) L(\cdot) L(⋅) 采用 softmax 形式和 loss-augmented step 函数形式时,本文的优化算法可以分别表示为交叉熵损失和 hinge 损失的梯度下降算法。
3.4 训练方法的细节
Minibatch 训练:
minibatch 训练准则在深度学习框架中应用广泛,比使用单个样本训练的过程更为稳定。
minibatch 训练有助于优化方法规避 “score-shift” 情况。
AP-loss 可以从一个 batch 中获得,也可以从具有多个 anchor 的单个图像中获得。
假设一个极端情况:我们的检测器可以同时预测 I 1 I_1 I1 和 I 2 I_2 I2 的完美 ranking,但是 I 1 I_1 I1 的最低得分都比 I 2 I_2 I2 的最高得分高,这就是两个图像的 “score-shift”,所以当单独计算每个图像的 AP-loss 时,会出现检测效果较差的情况。
计算一个 mini-batch 的所有图像的得分可以避免上述情况,所以 mini-batch 训练是保证好的收敛性和准确性的重要前提。
分段阶跃函数:
训练初期,得分 s i s_i si 之间非常接近(即几乎所有的 H(x)输入都接近于0),所以,输入的一个微小的改变将会带来一个大的输出改变,会改变更新过程。
为了避免该问题,我们使用下面的分段阶跃函数来代替 H ( x ) H(x) H(x) 函数:
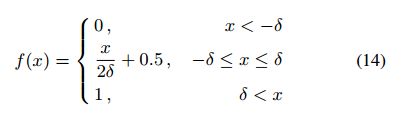
不同 δ \delta δ 情况下的分段阶跃函数如图4所示。
当 δ \delta δ 为 +0 时,该分段函数是最初的阶跃函数,注意, f ( ⋅ ) f(\cdot) f(⋅) 仅仅在输入接近于0的时候与 H ( ⋅ ) H(\cdot) H(⋅) 不同。
另外一个单调且对称的平滑函数同样有效,且仅仅在输入接近于0的时候与 H ( ⋅ ) H(\cdot) H(⋅) 不同。
δ \delta δ 的选择和 CNN 优化过程中的权值衰减有有着很大的联系。
δ \delta δ 决定了正样本和负样本的决策边界的宽度,小的 δ \delta δ 得到较窄的决策边界,会导致权值相应减小。
差值 AP 广泛用于目标检测基准数据的评估,如 PASCAL VOC 和 MS COCO。
4. 实验
4.1 实验设置
本文将提出的方法用于单阶段 RetinaNet [15] 上进行实验。
PASCAL VOC:
在 VOC2007 和 VOC2012 trainval 上进行训练,在 VOC2007 test 上进行评估
在 VOC2007 和 VOC2012 trainval + VOC2007 test 上进行训练,在 VOC2012 test 上进行测试。
此处,使用多个 IoU 阈值( 0:50 : 0:05 : 0:95)得到的 AP 的均值作为评估标准。
设置 Eq.14 中的 δ = 1 \delta=1 δ=1
将 RestNet 作为backbone模型,该模型在 ImageNet-1k 分类数据集上进行了预训练。
在每个层的 FPN,anchors 有 2 sub-ociave 尺度( 2 k / 2 2^{k/2} 2k/2 for k < = 1 k<=1 k<=1),和三个纵横比 [0.5, 1, 2]。
在训练阶段固定BN层
在 2 个 GPU 上使用 mini-batch 训练,每个 GPU 上处理8个图像。
所有模型的训练都迭代 160次,初始学习率为 0.001,在第110次和第140次分别下降10倍。
我们使用和 [18] 中相同的数据增强方式,在测试阶段未使用任何数据增强,训练阶段,输入图像大小固定为 512x512,测试阶段保持初始的纵横比,并将图像 resize ,来保证较短的边是600 pixels。
对每个类别,使用 NMS ,IoU 阈值为0.5。
MS COCO:
所有模型的训练都使用 trainval35k 集( 80k 训练,35k 个验证集中的数据),在 minival 集或 test-dev 上进行测试。
200个迭代次数,初始学习率 0.001,在第 60 次和第 80 次分别减小 10 倍。
4.2 消融学习
首先研究设置参数的影响:
4.2.1 不同参数的对比
此处研究以 3.4 节中的实验设置来进行实验的结果,见表1。
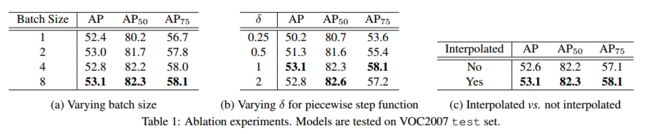
Minibatch Training:
分段阶跃函数:
Interpolated AP:
4.2.2 不同 loss 的对比
我们在 RetinaNet 上使用不同的 loss 来进行对比实验,结果见表2。
4.2.3 不同优化方法的对比
此处同样对不同的优化方法进行了对比:近似梯度方法 [34,9] 和结构化 hinge loss 方法 [20] 。
[34,9] 分别近似于使用平滑函数和包络函数的 AP-loss。
基于此,我们使用 sigmoid 函数代替阶跃函数,来保证梯度存在(非零且可计算)且不改变原始函数的相对大小。
与 [9] 相同,我们使用 log 域的目标函数,即 l o g ( A P + ϵ ) log(AP+\epsilon) log(AP+ϵ),来保证目标函数是有限的。
在 VOC2007 trainval set 上训练检测器,不执行 b-box 回归任务,收敛曲线见图 5b。
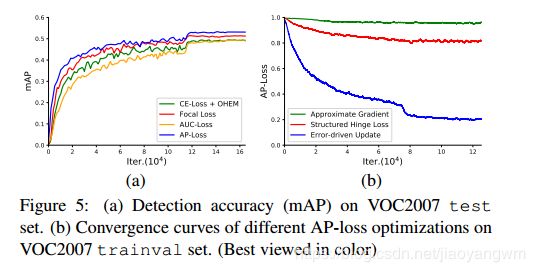
从图中可见,通过近似梯度方法来优化的 AP-loss 可能不收敛,这很可能由于非凸和非准凸性在直接梯度下降上中失败了。
同时,AP-loss 是用结构化的 hinge loss 来优化的,收敛缓慢且在近似 0.8 的地方稳定,这明显比我们的误差驱动更新方案优化的AP-loss的渐近极限差。我们认为该方法并没有直接优化AP-loss,而是由判别函数[20]控制AP-loss的一个上界。在排序任务中,这个判别函数是人工选择的,具有 AUC-like 的形式,这可能会导致优化的可变性。
4.3 基准结果
在消融研究中,我们选择了三个广泛使用的基准,对所提出的检测器与目前最先进的单级检测器进行了实验比较,包括 VOC2007 test, VOC2012 test and COCO 和 test-dev sets。
消融实验中,使用 ResNet-101 作为backbone,而非 ResNet-50,测试图像大小为 500x500。
表3 是不同的结果。
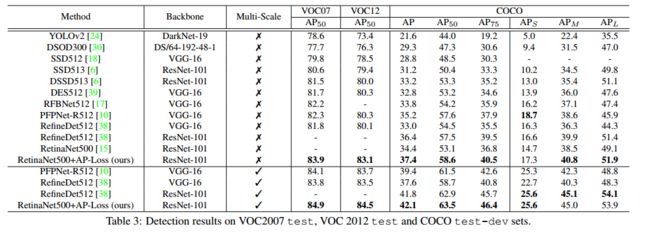
对比 RetinaNet500[15],在 COCO 数据集上本文的方法提升了 3.0%(37.4% vs. 34.4%)。
图6 呈现了使用 focal loss 和 AP-loss 训练 RetinaNet 的结果,本文的方法在这三个基准数据集中的单尺度和多尺度测试中都取得了优于其他方法的效果。

5. 结论
本文中,为了解决单阶段目标检测中的类别不平衡问题,将分类损失函数替换为排序函数,并且使用 AP-loss 来实现 ranking task。
由于 AP-loss 是不可微且非凸的,我们提出了一种新的方法——误差驱动更新机制,来优化该函数。
我们对所提出的方法进行了理论分析,实验结果表明,该方法可以显著提高现有单阶段检测器的性能。