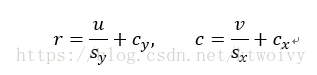#3D视觉#相机标定简介

目录

1.  相机和投影仪标定原理

2.  相机标定流程

3.  投影仪标定流程

 

 

1.  相机和投影仪标定原理

标定主要是解决从世界坐标系到相机坐标系，再到成像坐标之间的投影矩阵的关系，进而确定相机或投影仪的内参和外参。

涉及四个坐标，如图：

世界坐标系也称真实或现实世界坐标系，它是客观世界的绝对坐标。一般的3D场景都用这个坐标系来表示。

摄像机坐标系是以摄像机为中心制定的坐标系统，取摄像机的光轴做为z轴。

成像平面坐标系是指在摄像机内所形成的象平面坐标系统，即图像中的uv坐标系。成像平面与摄像机坐标系统的xy平面平行，这样成像平面原点就在摄像机的光轴(z轴)上。

图像坐标系是指在计算机内部数字图像所用的坐标系，文中即cr坐标系。图像坐标系与成像平面坐标系在同一平面上，图像坐标系包括图像物理坐标系(以毫米等为单位)和图像像素坐标系(以像素为单位)。

 

摄像机标定过程中各坐标系转换流程如下：

首先，世界坐标系中的一点，为了将其投影到成像平面上，需要首先将其转换到摄像机坐标系中。从世界坐标系到摄像机坐标系的变换由平移和旋转组成。

其中，是世界坐标系中的点，是摄像机坐标系中的点，是一个平移向量，即将世界坐标系的原点平移到摄像机坐标系的原点，是一个旋转矩阵。R和T的6个参数即为摄像机的外参。

接下来是将三维空间点从摄像机坐标系中投影到成像平面坐标系中，这个投影就是透视投影，公式为：

其中f是焦距。

投影到成像平面之后，镜头的畸变会导致（u,v）发生变化，需要进行校正，不过此时不需要三维信息了，畸变参数向量，前三个是径向，后两个是切向。

最后，将校正后的(u,v)从成像平面转换到图像坐标系中，坐标为(r,c)，公式为：

其中是图像主点，sx和sy是指图像传感器水平和垂直方向上相邻像素之间的距离。

所以总结来说，标定内参6个参数，确定摄像机如何实现三维空间点到二维图像点的映射。标定外参6个参数,决定了摄像机坐标系与世界坐标系之间的相对位置关系。

 

投影仪标定即将投影仪视为逆向相机，进行标定。重要的是获得单应性矩阵H，但是投影仪本身不具备捕捉图像的能力，需要借助相机建立模型。然后利用已知的点的物理坐标和像素坐标获得单应性矩阵，然后通过单应性矩阵寻找图像上投影点对应的物理坐标，最后利用该物理坐标和标准的棋盘投影图像的像素坐标标定得到摄像机内外参数。

 

2.  相机标定流程

第一步：采集不同位姿下的同一个棋盘格图像，如下所示

第二步：利用MATLAB相机标定工具箱进行初标定

安装工具箱之后，在命令框中输入calib，选择standard模式，出现如下界面：

然后将MATLAB运行路径设置在图像所在文件夹，依次点击Read images，按照指示读入图像，Extract grid corners，按照指示，对每张图像进行角点提取，注意MATLAB命令框中的提示，一般情况下选择默认的参数设置，即直接enter，往前运行，需要注意的是dX,dY的取值，按照实际棋盘个大小设置，例如本次用的棋盘是12mmx12mm。角点提取之后，点击Calibration，进行标定，得到初始的标定结果，如图。

可以看到，error较大，需要进一步优化。

第三步：优化标定结果。此步是MATLAB对比c++标定的优势，能根据误差分布，不断优化结果。

点击Analyse error，可以看到误差分布图，如下：

可以看到误差较大，而且分布并不集中。点击图中不集中的点，可以显示是由于哪一张图像引起的误差，例如：

接下来，点击Recomp.corners，重新选定窗大小和图像标号，然后点击calibration，可以看到误差不断变小。

最后变到某一比较满意的误差，分别也比较集中，即可认为标定结束。点击Save，保存标定结果。

本次使用的相机最终标定结果是：

 

3.  投影仪标定流程

投影仪标定使用的是c++程序。

第一步：采集图像如下：

周围的四个点用来求单应性矩阵，中心棋盘为投影所得。

第二步：检测图像中的四个圆圆心的位置，利用已知的物理坐标（以左上角点为圆心，建立坐标系）和检测得到的图像坐标，计算单应性矩阵。

 

第三步：检测图像中棋盘的角点，根据单应性矩阵，求得物理坐标。

第四步：根据标准的投影棋盘图像像素坐标，和投影变换所得的物理坐标，对投影仪进行标定。

生成棋盘所用数据如下图：

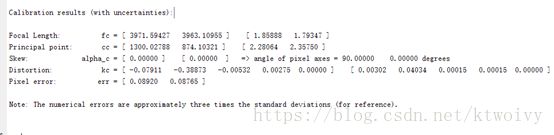
最终标定结果如下：

（该标定结果没有考虑投影图像的白边，实际上还需要确定白边像素尺寸，在程序中生成标准角点时加上这个像素）