详说Normalization(Batch Normalization,Layer Normalization,Instance Normalization,Group Normalization)

详说各种 Normalization

Batch Normalization 是 Sergey 等人于2015年在 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 中提出的一种归一化方法。

在开始讨论之前， 我们需要先探讨一个问题， 对于深度神经网络而言， 什么样的输入是一个好的输入，或者说什么样的输入可以又快又好的训练模型？ 通常我们希望输入的数据能够满足独立同分布，并且我们希望数据能分布在激活函数梯度较大的范围之内。可是在深度神经网络中，底层的参数更新会对高层的输入分布产生很大的影响，也就是说即使一开始我们的数据满足了要求，可是随着网络的传递，数据也会发生变化，不能满足要求。作者称这个现象叫 internal covariate shift。为了解决这个问题，作者提出了 Batch Normalization。

1. 什么是 Batch Normalization？

直接借用原文中的一副图来说明 Batch Normalization 的过程。
其中 $x_i$ 为输入数据， ${\mu }_{\beta }$ 为对一个 batch 的输入数据取平均值，${\sigma }_{\beta }^2$ 为方差，$\widehat{x_i}$ 是归一化之后的输入数据，其满足均值为 $0$， 方差为 $1$ ， 是一个标准正太分布。 其中 $ϵ$ 是一个很小的正数，仅仅是为了保证分母不为零。第四个方程是在 $\widehat{x_i}$ 基础上做了一个 $\gamma$ 倍的缩放 和 $\beta$ 的偏移。而这里的 $\gamma$ 和 $\beta$ 是超参数，也就是需要通过训练来的学习。

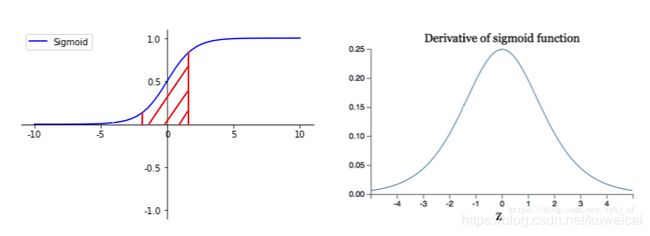
对于整个 Batch Normalization 的过程应该是非常清晰的，就是将输入的数据进行归一化，使其服从 均值为 $0$， 方差为 $1$ 的分布。唯一可能令人费解的是 为什么要进行第四个方程的操作？这里需要结合激活函数来说，比如对于 sigmoid 激活函数，归一化之后的数据输入 sigmoid 激活函数，会使数据落在近乎线性的区域(红色标记的区域仅仅是一个示意，并不严谨)，这个区域里 sigmoid 激活函数近乎于一个线性函数，实质上并不能起到非线性的作用，这样就不能起到拟合复杂系统的作用，当拟合能力弱了之后自然训练的结果也不会好。

那如何解决，作者通过第四步的操作，来解决这个问题。作者希望通过第四部将符合标准正态分布的数据变换会其原本的分布。

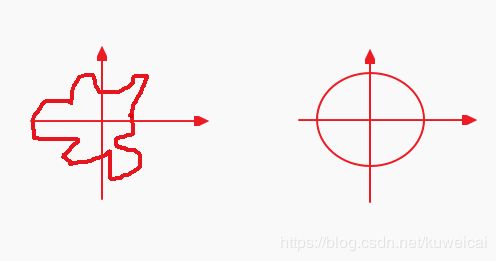
也许有人说又变回去了，那前面那些不是白整了吗？当然不是。下面的说法也许不够严谨，但是也可以说明这个问题，比如下面两批数据是同分布的，但是显然数据的结构并不相同，第二批数据明显更不容易过拟合。

2. Batch Normalization 有什么作用？

• a. 可以增大 learning rate， 使训练更快收敛
• b. 更不容易过拟合， 因此可以替代 dropout，或者少用 dropout，可以减少 L2 正则化的权重，同时可以减少 argument 的操作，可以不用太操心 initialization 的操作。

3. Batch Normalization 放在什么位置？

通常我们按照如下的位置:

Conv -> Batch Norm -> ReLU -> Pooling

当然也有人尝试如下的放置方法
Conv -> ReLU -> Batch Norm -> Pooling

4. Test 的时候均值和方差哪里来？

训练的时候我们每个 batch 都有均值和方差，可是 test 的时候呢？比如我就 test 一张图片。。。通常我们直接拿最后一次训练的时候的均值和方差。所以在实际应用时，需要计算并保存均值和方差信息。

5. 常用的 Normalization 方式有哪些？

5.1 Batch Normalization

Batch Normalization 上面已经介绍过了， 这里仅仅总结一下它的一些特性。

• batch normalization 和 batch size 紧密相关，当 batch size 比较小时，并不能得到好的统计数据，效果也就大打折扣。
• batch normalization 是以神经元为单位，计算每个神经元的所有输入的均值和方差
• batch normalization 需要存储均值和方差信息
• batch normalization 常用在固定深度的神经网络中， 比如 CNN
• batch normalization 对于深度不固定的网络， 比如 RNN， 通常计算会比较复杂

5.2 Layer Nornalization

Layer Normalization 是 Jimmy Lei Ba 等人（等人里面包括 Hinton）于 2016年 在 Layer Normalization 中提出的一种 normalization 的方法。
顾名思义，batch normalization 针对每个神经元的输入进行统计，而 layer normalization 则是在每个训练的样本下， 针对每个 layer 中的所有神经元的输入进行统计，得到的均值和方差作为一个规范，对该层的所有输入进行相同的规范化操作。

Layer Normalization 的特点如下。

• layer normalization 同一层的均值和方差相同， 不同的输入样本有不同的均值和方差
• layer normalization 训练和测试的时候进行相同的操作，不需要存储统计信息
• layer normalization 可以用于RNN， 或者是 batch size 较小的场合
• layer normalization 对于相似度较大的特征， 会降低模型的表示能力，此时 batch normalization 更优。

对比 batch normalization 和 layer normalization， 目前 batch normalization 使用更广，对于较大batch size的时候，batch normalization 的表现比 layer normalization好很多， 但是 layer normalization 具有更好适用性。

5.3 Weight Normalization

前面的 BN 和 LN 都是针对输入数据进行的 normalization， 而 WN 则是针对 weight 来进行归一化。WN不依赖于输入数据的分布，故可应用于mini-batch较小的情景且可用于动态网络结构。此外，WN还避免了LN中对每一层使用同一个规范化公式的不足。三种规范化方式尽管对输入数据的尺度化（scale）来源不同，但其本质上都实现了数据的规范化操作。

5.4 Instance Normalization

Instance Normalization(IN) 是 Dmitry Ulyanov 等人在 2016 年于 Instance Normalization: The Missing Ingredient for Fast Stylization 中提出的一种归一化方式。

在 GAN 和 style transfer 的任务中，目前的 IN 要好于 BN，IN 主要用于对单张图像的单个通道的数据做处理，而 BN 主要是对整个 Bacth 的数据做处理。由于BN在训练时每个 batch 的均值和方差会由于 shuffle 都会改变，所以可以理解为一种数据增强，而 IN 可以理解为对数据做一个归一化的操作。

更多可以参考 Batch normalization和Instance normalization的对比？。

5.5 Group Normalization

Group Normalization 是何凯明等人于 2018 年于 Group Normalization 提出的一种 normalization 方式。Group Normalization（GN）是针对Batch Normalization（BN）在batch size较小时错误率较高而提出的改进算法，因为BN层的计算结果依赖当前batch的数据，当batch size较小时（比如2、4这样），该batch数据的均值和方差的代表性较差，因此对最后的结果影响也较大。GN 根据通道进行分组，然后在每个组内做归一化，计算器均值和方差，从而不受批次中样本数量的约束。这里将通道分为 G 组，G 是一个超参数，通常为 默认为32。

如下图所示，随着batch size越来越小，BN层所计算的统计信息的可靠性越来越差，这样就容易导致最后错误率的上升；而在batch size较大时则没有明显的差别。虽然在分类算法中一般的GPU显存都能cover住较大的batch设置，但是在目标检测、分割以及视频相关的算法中，由于输入图像较大、维度多样以及算法本身原因等，batch size一般都设置比较小，所以GN对于这种类型算法的改进应该比较明显。

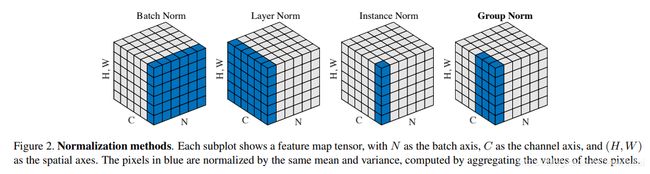
通过下面的对比图可以清晰的看到，GN 是介于 LN 和 IN直接的一种归一化方式。可以看出BN的计算和 batch size 相关（蓝色区域为计算均值和方差的单元），而 LN、BN 和 GN 的计算和 batch size 无关。同时 LN 和 IN 都可以看作是 GN 的特殊情况（LN是group=C时候的GN，IN是group=1时候的GN）。

上图中，从C方向看过去是指一个个通道，从N看过去是一张张图片。每6个竖着排列的小正方体组成的长方体代表一张图片的一个feature map。蓝色的方块是一起进行Normalization的部分。由此就可以很清楚的看出，Batch Normalization是指6张图片中的每一张图片的同一个通道一起进行Normalization操作。而Instance Normalization是指单张图片的单个通道单独进行Noramlization操作。

更多内容可以参考全面解读Group Normalization-（吴育昕-何恺明) 。