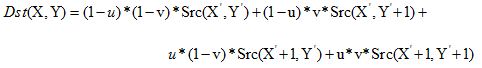数字图像的缩放及opencv中的实现
1. 数字图像的缩放
常用的数字图像的缩放的方式有最近邻插值、双线性插值、双三次插值。
最近邻插值就是把目标图像的像素点映射到原图像中,那个像素离得最近,就把目标图像中的像素值取为该点的值。
双线性插值是指考虑两个方向(X & Y),四个像素点来计算目标图像中的像素值。和最近邻相比,每个双线性不仅考虑了两个方向,并且每个方向上考虑了目标像素与原像素点的距离的加权。双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
关于最近邻和双线性插值的原理可以参考下面两篇博客,里面的讲解通俗易懂。
http://blog.csdn.net/andrew659/article/details/4818988
http://blog.csdn.net/qq_20823641/article/details/52221442
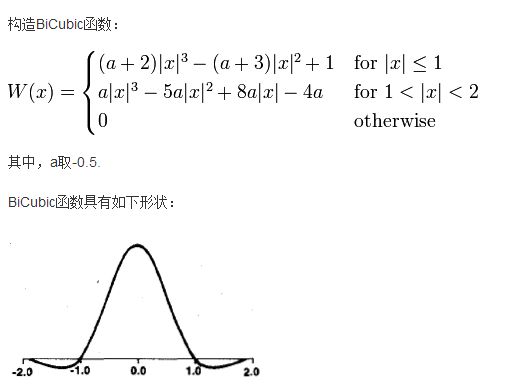
双三次插值则可以看成是考虑了更大范围(16“邻域”)的一种加权来计算目标像素点的像素值。相比双线性计算量更大了,当然也取得了更平滑的边缘。
2.opencv中图像缩放API
opencv中提供了resize()来对图像进行缩放。但是其提供了五种插值方式供选择,除了刚刚提到的三种还有INTER_AERE(区域插值)和INTER_LANCZOS4(兰索斯插值)。下面是官方文档。根据官方文档,对于缩小图像,一般情况下最好用CV_INTER_AREA,而对于放大图像,一般情况下最好用CV_INTER_CUBIC(效率不高,慢) 或 CV_INTER_LINEAR(效率较高,速度较快)。
C++: void resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, intinterpolation=INTER_LINEAR )
| Parameters: |
|
|---|
fx & fy默认值为0,interpolation 默认值为1(INTER_LINEAR),INTER_NEAREST==0,INTER_CUBIC==2, INTER_AREA==3,INTER_LANCZOS4==4
下面用for循环代替cv::resize函数来说明其详细的插值实现过程,其中部分代码摘自于cv::resize函数中的源代码。
每种插值算法的前部分代码是相同的,如下:
cv::Mat matSrc, matDst1, matDst2;
matSrc = cv::imread("lena.jpg", 2 | 4); //载入无损的源图像
matDst1 = cv::Mat(cv::Size(800, 1000), matSrc.type(), cv::Scalar::all(0));
matDst2 = cv::Mat(matDst1.size(), matSrc.type(), cv::Scalar::all(0));
double scale_x = (double)matSrc.cols / matDst1.cols;//x方向的缩放因子
double scale_y = (double)matSrc.rows / matDst1.rows;//y方向的缩放因子
2.1、最近邻:公式,
for (int i = 0; i < matDst1.cols; ++i)//以目标图像为基准,映射到源图像中
{
int sx = cvFloor(i * scale_x); //向下取整
sx = std::min(sx, matSrc.cols - 1); //防止超出源图像的边界
for (int j = 0; j < matDst1.rows; ++j)
{
int sy = cvFloor(j * scale_y);
sy = std::min(sy, matSrc.rows - 1); //防止超出源图像的边界
matDst1.at(j, i) = matSrc.at(sy, sx);
}
}
cv::imwrite("nearest_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 0);
cv::imwrite("nearest_2.jpg", matDst2); 2.2、双线性:由相邻的四像素(2*2)计算得出,公式,
char* dataDst = matDst1.data;
int stepDst = matDst1.step;//每一行像素数据所占的字节数
uchar* dataSrc = matSrc.data;
int stepSrc = matSrc.step;
int iWidthSrc = matSrc.cols;
int iHiehgtSrc = matSrc.rows;
for (int j = 0; j < matDst1.rows; ++j)
{
float fy = (float)((j + 0.5) * scale_y - 0.5);
int sy = cvFloor(fy); //sy为fy的整数部分(向下取整)
fy -= sy; //fy更新为fy的小数部分
sy = std::min(sy, iHeihgtSrc - 2); //防止sy越上界
sy = std::max(0, sy); //防止sy越下界
short cbufy[2];
cbufy[0] = cv::saturate_cast((1.f - fy) * 2048);
cbufy[1] = 2048 - cbufy[0];
for (int i = 0; i < matDst1.cols; ++i)
{
float fx = (float)((i + 0.5) * scale_x - 0.5);
int sx = cvFloor(fx);//sx为fx的整数部分(向下取整)
fx -= sx;//fx更新为fx的小数部分
if (sx < 0) {
fx = 0, sx = 0;
}
if (sx >= iWidthSrc - 1) {
fx = 0, sx = iWidthSrc - 2;
}
short cbufx[2];
cbufx[0] = cv::saturate_cast((1.f - fx) * 2048);
cbufx[1] = 2048 - cbufx[0];
//由于cbufx[0]和cbufy[1]都放大了2048(2^11)倍,这里右移是为了还原,
//这样先乘后右移的操作在图像处理中很常见,主要是为了简化计算
for (int k = 0; k < matSrc.channels(); ++k)
{
*(dataDst+ j*stepDst + 3*i + k) = (*(dataSrc + sy*stepSrc + 3*sx + k) * cbufx[0] * cbufy[0] +
*(dataSrc + (sy+1)*stepSrc + 3*sx + k) * cbufx[0] * cbufy[1] +
*(dataSrc + sy*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[0] +
*(dataSrc + (sy+1)*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[1]) >> 22;
}
}
}
cv::imwrite("linear_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 1); //调用resize()中的双线性插值
cv::imwrite("linear_2.jpg", matDst2); 2.3 双三次
下面的代码中a取-0.75
int iscale_x = cv::saturate_cast(scale_x);
int iscale_y = cv::saturate_cast(scale_y);
for (int j = 0; j < matDst1.rows; ++j)
{
float fy = (float)((j + 0.5) * scale_y - 0.5);
int sy = cvFloor(fy);
fy -= sy;
sy = std::min(sy, matSrc.rows - 3);
sy = std::max(1, sy);
const float A = -0.75f;
float coeffsY[4];
coeffsY[0] = ((A*(fy + 1) - 5*A)*(fy + 1) + 8*A)*(fy + 1) - 4*A;
coeffsY[1] = ((A + 2)*fy - (A + 3))*fy*fy + 1;
coeffsY[2] = ((A + 2)*(1 - fy) - (A + 3))*(1 - fy)*(1 - fy) + 1;
coeffsY[3] = 1.f - coeffsY[0] - coeffsY[1] - coeffsY[2];
short cbufY[4];
cbufY[0] = cv::saturate_cast(coeffsY[0] * 2048);
cbufY[1] = cv::saturate_cast(coeffsY[1] * 2048);
cbufY[2] = cv::saturate_cast(coeffsY[2] * 2048);
cbufY[3] = cv::saturate_cast(coeffsY[3] * 2048);
for (int i = 0; i < matDst1.cols; ++i)
{
float fx = (float)((i + 0.5) * scale_x - 0.5);
int sx = cvFloor(fx);
fx -= sx;
if (sx < 1) {
fx = 0, sx = 1;
}
if (sx >= matSrc.cols - 3) {
fx = 0, sx = matSrc.cols - 3;
}
float coeffsX[4];
coeffsX[0] = ((A*(fx + 1) - 5*A)*(fx + 1) + 8*A)*(fx + 1) - 4*A;
coeffsX[1] = ((A + 2)*fx - (A + 3))*fx*fx + 1;
coeffsX[2] = ((A + 2)*(1 - fx) - (A + 3))*(1 - fx)*(1 - fx) + 1;
coeffsX[3] = 1.f - coeffsX[0] - coeffsX[1] - coeffsX[2];
short cbufX[4];
cbufX[0] = cv::saturate_cast(coeffsX[0] * 2048);
cbufX[1] = cv::saturate_cast(coeffsX[1] * 2048);
cbufX[2] = cv::saturate_cast(coeffsX[2] * 2048);
cbufX[3] = cv::saturate_cast(coeffsX[3] * 2048);
for (int k = 0; k < matSrc.channels(); ++k)
{
matDst1.at(j, i)[k] = abs((matSrc.at(sy-1, sx-1)[k] * cbufX[0] * cbufY[0] + matSrc.at(sy, sx-1)[k] * cbufX[0] * cbufY[1] +
matSrc.at(sy+1, sx-1)[k] * cbufX[0] * cbufY[2] + matSrc.at(sy+2, sx-1)[k] * cbufX[0] * cbufY[3] +
matSrc.at(sy-1, sx)[k] * cbufX[1] * cbufY[0] + matSrc.at(sy, sx)[k] * cbufX[1] * cbufY[1] +
matSrc.at(sy+1, sx)[k] * cbufX[1] * cbufY[2] + matSrc.at(sy+2, sx)[k] * cbufX[1] * cbufY[3] +
matSrc.at(sy-1, sx+1)[k] * cbufX[2] * cbufY[0] + matSrc.at(sy, sx+1)[k] * cbufX[2] * cbufY[1] +
matSrc.at(sy+1, sx+1)[k] * cbufX[2] * cbufY[2] + matSrc.at(sy+2, sx+1)[k] * cbufX[2] * cbufY[3] +
matSrc.at(sy-1, sx+2)[k] * cbufX[3] * cbufY[0] + matSrc.at(sy, sx+2)[k] * cbufX[3] * cbufY[1] +
matSrc.at(sy+1, sx+2)[k] * cbufX[3] * cbufY[2] + matSrc.at(sy+2, sx+2)[k] * cbufX[3] * cbufY[3] ) >> 22);
}
}
}
cv::imwrite("cubic_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 2);
cv::imwrite("cubic_2.jpg", matDst2); 2.4 基于像素区域关系:共分三种情况,图像放大时类似于最近邻插值,图像缩小(x轴、y轴同时缩小)又分两种情况,此情况下可以避免波纹出现。
看了fengbingchun的博客,但是感觉这一段有问题,等什么时候自己把源代码翻出来看看吧
2.5 兰索斯插值:由相邻的8*8像素计算得出,公式类似于双线性
int iscale_x = cv::saturate_cast(scale_x);
int iscale_y = cv::saturate_cast(scale_y);
for (int j = 0; j < matDst1.rows; ++j)
{
float fy = (float)((j + 0.5) * scale_y - 0.5);
int sy = cvFloor(fy);
fy -= sy;
sy = std::min(sy, matSrc.rows - 5);
sy = std::max(3, sy);
const double s45 = 0.70710678118654752440084436210485;
const double cs[][2] = {{1, 0}, {-s45, -s45}, {0, 1}, {s45, -s45}, {-1, 0}, {s45, s45}, {0, -1}, {-s45, s45}};
float coeffsY[8];
if (fy < FLT_EPSILON)
{
for (int t = 0; t < 8; t++)
coeffsY[t] = 0;
coeffsY[3] = 1;
}
else
{
float sum = 0;
double y0 = -(fy + 3) * CV_PI * 0.25, s0 = sin(y0), c0 = cos(y0);
for (int t = 0; t < 8; ++t)
{
double dy = -(fy + 3 -t) * CV_PI * 0.25;
coeffsY[t] = (float)((cs[t][0] * s0 + cs[t][1] * c0) / (dy * dy));
sum += coeffsY[t];
}
sum = 1.f / sum;
for (int t = 0; t < 8; ++t)
coeffsY[t] *= sum;
}
short cbufY[8];
cbufY[0] = cv::saturate_cast(coeffsY[0] * 2048);
cbufY[1] = cv::saturate_cast(coeffsY[1] * 2048);
cbufY[2] = cv::saturate_cast(coeffsY[2] * 2048);
cbufY[3] = cv::saturate_cast(coeffsY[3] * 2048);
cbufY[4] = cv::saturate_cast(coeffsY[4] * 2048);
cbufY[5] = cv::saturate_cast(coeffsY[5] * 2048);
cbufY[6] = cv::saturate_cast(coeffsY[6] * 2048);
cbufY[7] = cv::saturate_cast(coeffsY[7] * 2048);
for (int i = 0; i < matDst1.cols; ++i)
{
float fx = (float)((i + 0.5) * scale_x - 0.5);
int sx = cvFloor(fx);
fx -= sx;
if (sx < 3)
{
fx = 0, sx = 3;
}
if (sx >= matSrc.cols - 5)
{
fx = 0, sx = matSrc.cols - 5;
}
float coeffsX[8];
if (fx < FLT_EPSILON)
{
for ( int t = 0; t < 8; t++ )
coeffsX[t] = 0;
coeffsX[3] = 1;
}
else
{
float sum = 0;
double x0 = -(fx + 3) * CV_PI * 0.25, s0 = sin(x0), c0 = cos(x0);
for (int t = 0; t < 8; ++t)
{
double dx = -(fx + 3 -t) * CV_PI * 0.25;
coeffsX[t] = (float)((cs[t][0] * s0 + cs[t][1] * c0) / (dx * dx));
sum += coeffsX[t];
}
sum = 1.f / sum;
for (int t = 0; t < 8; ++t)
coeffsX[t] *= sum;
}
short cbufX[8];
cbufX[0] = cv::saturate_cast(coeffsX[0] * 2048);
cbufX[1] = cv::saturate_cast(coeffsX[1] * 2048);
cbufX[2] = cv::saturate_cast(coeffsX[2] * 2048);
cbufX[3] = cv::saturate_cast(coeffsX[3] * 2048);
cbufX[4] = cv::saturate_cast(coeffsX[4] * 2048);
cbufX[5] = cv::saturate_cast(coeffsX[5] * 2048);
cbufX[6] = cv::saturate_cast(coeffsX[6] * 2048);
cbufX[7] = cv::saturate_cast(coeffsX[7] * 2048);
for (int k = 0; k < matSrc.channels(); ++k)
{
matDst1.at(j, i)[k] = abs((matSrc.at(sy-3, sx-3)[k] * cbufX[0] * cbufY[0] + matSrc.at(sy-2, sx-3)[k] * cbufX[0] * cbufY[1] +
matSrc.at(sy-1, sx-3)[k] * cbufX[0] * cbufY[2] + matSrc.at(sy, sx-3)[k] * cbufX[0] * cbufY[3] +
matSrc.at(sy+1, sx-3)[k] * cbufX[0] * cbufY[4] + matSrc.at(sy+2, sx-3)[k] * cbufX[0] * cbufY[5] +
matSrc.at(sy+3, sx-3)[k] * cbufX[0] * cbufY[6] + matSrc.at(sy+4, sx-3)[k] * cbufX[0] * cbufY[7] +
matSrc.at(sy-3, sx-2)[k] * cbufX[1] * cbufY[0] + matSrc.at(sy-2, sx-2)[k] * cbufX[1] * cbufY[1] +
matSrc.at(sy-1, sx-2)[k] * cbufX[1] * cbufY[2] + matSrc.at(sy, sx-2)[k] * cbufX[1] * cbufY[3] +
matSrc.at(sy+1, sx-2)[k] * cbufX[1] * cbufY[4] + matSrc.at(sy+2, sx-2)[k] * cbufX[1] * cbufY[5] +
matSrc.at(sy+3, sx-2)[k] * cbufX[1] * cbufY[6] + matSrc.at(sy+4, sx-2)[k] * cbufX[1] * cbufY[7] +
matSrc.at(sy-3, sx-1)[k] * cbufX[2] * cbufY[0] + matSrc.at(sy-2, sx-1)[k] * cbufX[2] * cbufY[1] +
matSrc.at(sy-1, sx-1)[k] * cbufX[2] * cbufY[2] + matSrc.at(sy, sx-1)[k] * cbufX[2] * cbufY[3] +
matSrc.at(sy+1, sx-1)[k] * cbufX[2] * cbufY[4] + matSrc.at(sy+2, sx-1)[k] * cbufX[2] * cbufY[5] +
matSrc.at(sy+3, sx-1)[k] * cbufX[2] * cbufY[6] + matSrc.at(sy+4, sx-1)[k] * cbufX[2] * cbufY[7] +
matSrc.at(sy-3, sx)[k] * cbufX[3] * cbufY[0] + matSrc.at(sy-2, sx)[k] * cbufX[3] * cbufY[1] +
matSrc.at(sy-1, sx)[k] * cbufX[3] * cbufY[2] + matSrc.at(sy, sx)[k] * cbufX[3] * cbufY[3] +
matSrc.at(sy+1, sx)[k] * cbufX[3] * cbufY[4] + matSrc.at(sy+2, sx)[k] * cbufX[3] * cbufY[5] +
matSrc.at(sy+3, sx)[k] * cbufX[3] * cbufY[6] + matSrc.at(sy+4, sx)[k] * cbufX[3] * cbufY[7] +
matSrc.at(sy-3, sx+1)[k] * cbufX[4] * cbufY[0] + matSrc.at(sy-2, sx+1)[k] * cbufX[4] * cbufY[1] +
matSrc.at(sy-1, sx+1)[k] * cbufX[4] * cbufY[2] + matSrc.at(sy, sx+1)[k] * cbufX[4] * cbufY[3] +
matSrc.at(sy+1, sx+1)[k] * cbufX[4] * cbufY[4] + matSrc.at(sy+2, sx+1)[k] * cbufX[4] * cbufY[5] +
matSrc.at(sy+3, sx+1)[k] * cbufX[4] * cbufY[6] + matSrc.at(sy+4, sx+1)[k] * cbufX[4] * cbufY[7] +
matSrc.at(sy-3, sx+2)[k] * cbufX[5] * cbufY[0] + matSrc.at(sy-2, sx+2)[k] * cbufX[5] * cbufY[1] +
matSrc.at(sy-1, sx+2)[k] * cbufX[5] * cbufY[2] + matSrc.at(sy, sx+2)[k] * cbufX[5] * cbufY[3] +
matSrc.at(sy+1, sx+2)[k] * cbufX[5] * cbufY[4] + matSrc.at(sy+2, sx+2)[k] * cbufX[5] * cbufY[5] +
matSrc.at(sy+3, sx+2)[k] * cbufX[5] * cbufY[6] + matSrc.at(sy+4, sx+2)[k] * cbufX[5] * cbufY[7] +
matSrc.at(sy-3, sx+3)[k] * cbufX[6] * cbufY[0] + matSrc.at(sy-2, sx+3)[k] * cbufX[6] * cbufY[1] +
matSrc.at(sy-1, sx+3)[k] * cbufX[6] * cbufY[2] + matSrc.at(sy, sx+3)[k] * cbufX[6] * cbufY[3] +
matSrc.at(sy+1, sx+3)[k] * cbufX[6] * cbufY[4] + matSrc.at(sy+2, sx+3)[k] * cbufX[6] * cbufY[5] +
matSrc.at(sy+3, sx+3)[k] * cbufX[6] * cbufY[6] + matSrc.at(sy+4, sx+3)[k] * cbufX[6] * cbufY[7] +
matSrc.at(sy-3, sx+4)[k] * cbufX[7] * cbufY[0] + matSrc.at(sy-2, sx+4)[k] * cbufX[7] * cbufY[1] +
matSrc.at(sy-1, sx+4)[k] * cbufX[7] * cbufY[2] + matSrc.at(sy, sx+4)[k] * cbufX[7] * cbufY[3] +
matSrc.at(sy+1, sx+4)[k] * cbufX[7] * cbufY[4] + matSrc.at(sy+2, sx+4)[k] * cbufX[7] * cbufY[5] +
matSrc.at(sy+3, sx+4)[k] * cbufX[7] * cbufY[6] + matSrc.at(sy+4, sx+4)[k] * cbufX[7] * cbufY[7] ) >> 22);// 4194304
}
}
}
cv::imwrite("Lanczos_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 4);
cv::imwrite("Lanczos_2.jpg", matDst2);