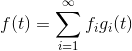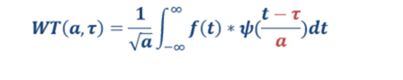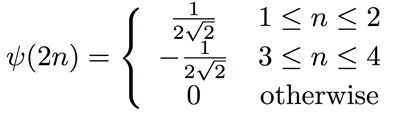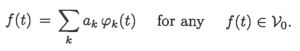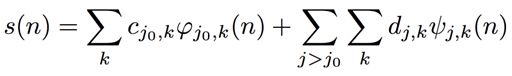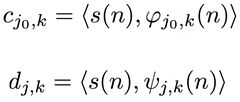小波变换
小波,一个神奇的波,可长可短可胖可瘦(伸缩平移),当去学习小波的时候,第一个首先要做的就是回顾傅立叶变换(又回来了,唉),因为他们都是频率变换的方法,而傅立叶变换是最入门的,也是最先了解的,通过傅立叶变换,了解缺点,改进,慢慢的就成了小波变换。主要的关键的方向是傅立叶变换、短时傅立叶变换,小波变换等,第二代小波的什么的就不说了,太多了没太多意义。当然,其中会看到很多的名词,例如,内积,基,归一化正交,投影,Hilbert空间,多分辨率,父小波,母小波,这些不同的名词也是学习小波路上的标志牌,所以在刚学习小波变换的时候,看着三个方向和标志牌,可以顺利的走下去,当然路上的美景要自己去欣赏(这里的美景就是定义和推导了)。因为内容太多,不是很重要的地方我都注释为(查定义)一堆文字的就是理论(可以大体一看不用立刻就懂),同时最下面也给了几个网址辅助学习。
一、基
傅立叶变换和小波变换,都会听到分解和重构,其中这个就是根本,因为他们的变化都是将信号看成由若干个东西组成的,而且这些东西能够处理还原成比原来更好的信号。那怎么分解呢?那就需要一个分解的量,也就是常说的基,基的了解可以类比向量,向量空间的一个向量可以分解在x,y方向,同时在各个方向定义单位向量e1、e2,这样任意一个向量都可以表示为a=xe1+ye2,这个是二维空间的基,
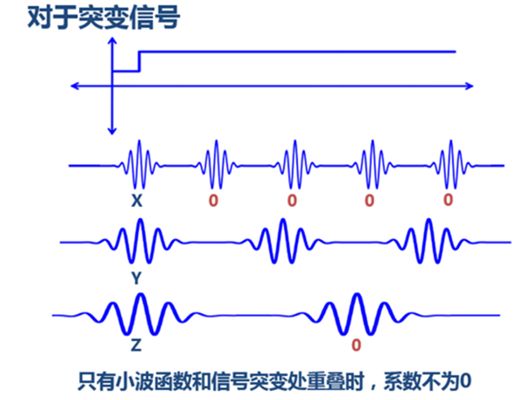
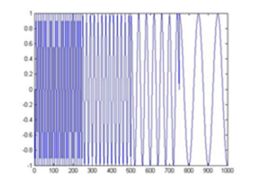
而对于傅立叶变换的基是不同频率的正弦曲线,所以傅立叶变换是把信号波分解成不同频率的正弦波的叠加和,而对于小波变换就是把一个信号分解成一系列的小波,这里时候,也许就会问,小波变换的小波是什么啊,定义中就是告诉我们小波,因为这个小波实在是太多,一个是种类多,还有就是同一种小波还可以尺度变换,但是小波在整个时间范围的幅度平均值是0,具有有限的持续时间和突变的频率和振幅,可以是不规则,也可以是不对称,很明显正弦波就不是小波,什么的是呢,看下面几个图就是
当有了基,以后有什么用呢?
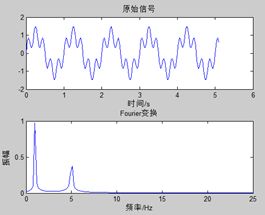
下面看一个傅立叶变换的实例:
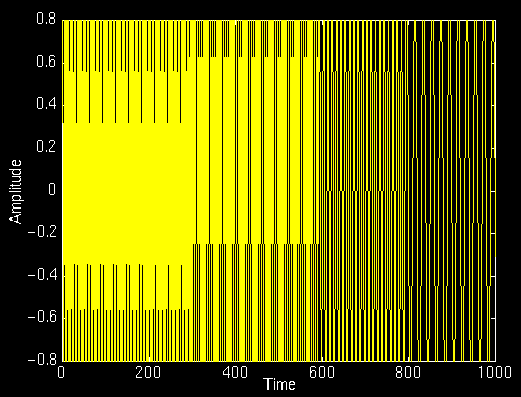
对于一个信号的表达式为x=sin(2*pi*t)+0.5*sin(2*pi*5*t);
这里可以看到是他的基就是sin函数,频率是1和5,下面看看图形的表示,是不是感受了到了频域变换给人的一目了然。
基具有非冗余性,即使基不是正交的,有相关性,但若去掉其中任何一个,则不成为基,这一点也叫完备性;基的表示有唯一性,即给定一族基对一个函数的表达是唯一的;一般情况下基非正交,也称为为exact frame(Resize basis),这个时候要表示信号可以将基正交化成唯一的正交基(对偶为其自身);也可以求其对偶框架(dual frame),其对应了小波变换中的双正交情形!信号可以依框架分解,然后用对偶框架重构。若在基集里添加一些新的向量,并随意调整空间位置,则有可能成为框架。把函数与基或框架作内积,也可以说成是一种函数空间到系数空间的变换。若某种变换后的能量(内积的平方和度量)仍然有一个大于0的上下界,才可以成为框架,由于框架的冗余性,所以系数的表达也不具有唯一性。若上下界相等,则为紧框架,且界表示冗余度。若上下界相等为且为1,称为pasval identity frame,此时不一定为正交基(想象把一组正交基中某一个拆成两个同方向的基之和,则pasval identity仍然成立),此时若加上基的长度均为一的条件,则框架退化为正交基。可能你会问我们用基来表示信号就行了啊,为什么还要框架呢?其实很多信号表示方法不能构成基,却能构成框架,如短时傅立叶变换中如要求窗函数满足基条件,则可推出该函数有很差的时频局部化性质(事实上退化为了傅立叶变换。
二、内积
在Hilbert空间(查定义)里看到这个东西,用来刻画两个向量的夹角,当内积为0时,两个向量正交,若g为Hilbert空间里的正交基的时候,内积为f向基上的正交投影;(Hilbert空间是一个很直观的空间,我一直都理解为欧氏空间去理解定义在其上的东西,L^2(平方可积,查定义)和l^2同样为Hilbert空间。
下面这个公式是基本,经过变形后会用在推导中:
如果两个向量的内积为0 ,就说他们是正交的。
如果一个向量序列相互对偶正交,并且长度都为1,那么就说他们是正交归一化的。
对于![]() ,存在L2(R)上一组标准正交基gi(t),i=1,2,3….,使得
,存在L2(R)上一组标准正交基gi(t),i=1,2,3….,使得
L2(R)上任意一个函数f(t)都可以由L2(R)上的一个规范正交基gi(t)进行线性组合表示出来
三、傅立叶的缺点
先列举出来缺点,然后再说明:
(1) Fourier分析不能刻画时间域上信号的局部特性
(2) Fourier分析对突变和非平稳信号的效果不好,没有时频分析
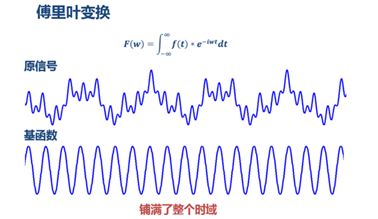
傅立叶变换傅立叶变换将函数投影到三角波上,将函数分解成了不同频率的三角波,这不能不说是一个伟大的发现,但是在大量的应用中,傅立叶变换的局限性却日趋明显,事实上在光滑平稳信号的表示中,傅立叶基已经达到了近似最优表示,但是日常生活中的信号却并不是一直光滑的,而且奇异是平凡的,傅立叶在奇异点的表现就着实让人不爽,从对方波的傅立叶逼近就可以看出来,用了大量不同频率的三角波去逼近其系数衰减程度相当缓慢,而且会产生Gibbs效应。其内在的原因是其基为全局性基,没有局部化能力,以至局部一个小小的摆动也会影响全局的系数。实际应用中很需要时频局部化,傅立叶显然缺乏此能力了。即使如此,由于其鲜明的物理意义和快速计算,在很多场合仍然应用广泛。傅立叶变换在从连续到离散的情形是值得借鉴与学习的,大家都知道,时间周期对应频域离散,时间离散对应频域周期,时间离散周期对应频域离散 周期,DFT其实是将离散信号做周期延拓然后做傅立叶变换再截取一个周期,反变换同样如此,所以DFT用的是块基的概念,这样如果信号两端的信号连接后不再光滑(即使两边都光滑),同样会在边界上产生大幅值系数(边界效应),延伸到图像中就是块效应。当对信号做对称周期延拓后再做傅立叶变换得到的正弦系数全部为0,也就是任何对称函数可以写成余弦的线性组合,同样按照离散的思路构造得到的是离散块余弦基,即DCT变换,虽然DCT可以通过对称后周期延拓再变换减少了边界效应(两边信号接上了,但不一定平滑),但任不能消除块效应,尤其是图像变换中人为将图像分成8*8处理后块效应更加明显。但是DCT很好的能量聚集效应让人惊奇,加之快速计算方法使它替代DFT成为图像的压缩的标准了很长时间(JPEG)。
上面一堆文字也许看的有点蒙,还是用图来说明
第一个就是傅立叶变换是整个时域,所以没有局部特征,这个也是他的基函数决定的看图,同时如果在时域张有了突变,那么在频域就需要大量的三角波去拟合,这也是傅立叶变换性质决定的。
第二个就是面对非平稳信号,傅立叶变换可以看到由哪些频域组成,但是不知道各成分对应的时刻是什么,也就是没有时频分析,看不出来信号频域随着时间变换的情况,反过来说就是,一个的频图对应好几个时域图,不知道是哪个,这个在实际应用中就不好了,看图
做FFT后,我们发现这三个时域上有巨大差异的信号,频谱(幅值谱)却非常一致。尤其是下边两个非平稳信号,我们从频谱上无法区分它们,因为它们包含的四个频率的信号的成分确实是一样的,只是出现的先后顺序不同。
可见,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
然而平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的,所以在比如生物医学信号分析等领域的论文中,基本看不到单纯傅里叶变换这样naive的方法。
上图所示的是一个正常人的事件相关电位。对于这样的非平稳信号,只知道包含哪些频率成分是不够的,我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——这也就是时频分析。
三、短时傅立叶变换(Short-time Fourier Transform,STFT)
有了缺点就要改进了,这里就出来了短时傅立叶变换,也叫加窗傅立叶变换,顾名思义,就是因为傅立叶变换的时域太长了,所以要弄短一点,这样就有了局部性。
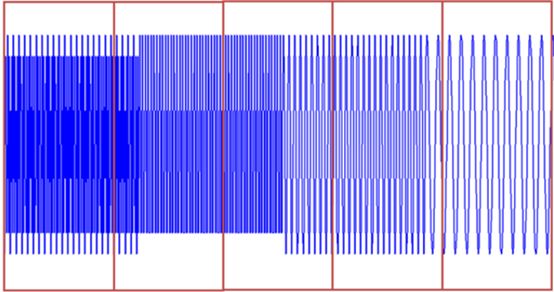
定义:把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。下面就是示意图
时域上分成一段一段做FFT,不就知道频率成分随着时间的变化情况了吗!
可能理解这一点最好的方式是举例子。首先,因为我们的变换是对时间和频率的函数(不像傅立叶变换,仅仅是对频率的函数),它是二维的(如果加上幅度则是三维)。以下图所示的非平稳信号为例:
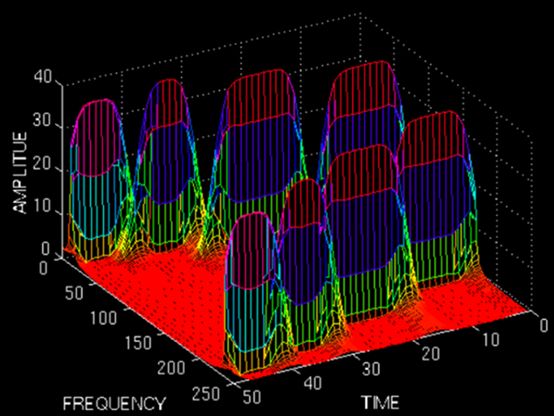
在这个信号中,在不同时刻有四个频率分量。0-250ms内信号的频率为300Hz,其余每个250ms的间隔的信号频率分别为200Hz,100Hz和50Hz。很明显,这是一个非平稳信号,让我们看一看它的短时傅立叶变换:用这样的方法,可以得到一个信号的时频图了:
图上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四个频域成分,还能看到出现的时间。两排峰是对称的,所以大家只用看一排就行了。
看着貌似解决了问题,好像有了局部性,但是这个名字叫做加窗傅立叶变换,那么这个窗要多大了呢?
窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差。
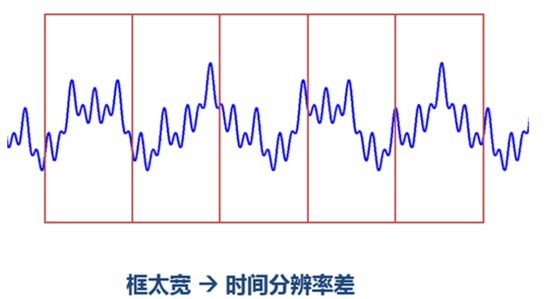
窗太宽,时域上又不够精细,时间分辨率低。
(这里插一句,这个道理可以用海森堡不确定性原理来解释。类似于我们不能同时获取一个粒子的动量和位置,我们也不能同时获取信号绝对精准的时刻和频率。这也是一对不可兼得的矛盾体。我们不知道在某个瞬间哪个频率分量存在,我们知道的只能是在一个时间段内某个频带的分量存在。所以绝对意义的瞬时频率是不存在的。)
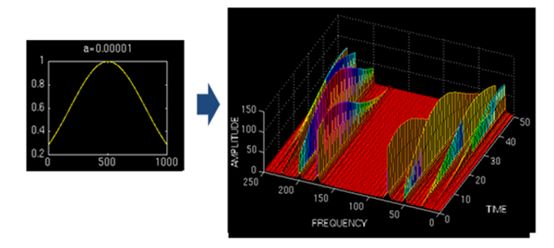
上图对同一个信号(4个频率成分)采用不同宽度的窗做STFT,结果如右图。用窄窗,时频图在时间轴上分辨率很高,几个峰基本成矩形,而用宽窗则变成了绵延的矮山。但是频率轴上,窄窗明显不如下边两个宽窗精确。
所以窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。
对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。
四、小波变换
真是千呼万唤才出来了,终于看见小波了啊。
这里先引入小波,回顾一下基,然后再看看小波的优点,其实就是上面傅立叶缺点的解决。
对于加窗傅立叶变换让人头疼的就是窗口的大小问题,如果我们让窗口的大小可以改变,不就完美了吗?答案是肯定的,小波就是基于这个思路,但是不同的是。STFT是给信号加窗,分段做FFT;而小波变换并没有采用窗的思想,更没有做傅里叶变换。小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了~
这里就又回到了最开始的基了。
这个基函数会伸缩、会平移(其实是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系。那么我们就知道信号包含该频率的成分的多少。如前边所说,小波做的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基。效果如下图
现在来看一下小波公式
从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。如下图
当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。
而当我们在每个尺度下都平移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。
看到了吗?有了小波,我们从此再也不害怕非稳定信号啦!从此可以做时频分析啦!
(1) 解决了局部性
(2)解决时频分析
做傅里叶变换只能得到一个频谱,做小波变换却可以得到一个时频谱!
时域信号 傅立叶变换结果 小波变换结果
五、小波的深入
上面那么多,也就是走进小波的大门,具体的我们还要学习子空间、多分辨率,母小波的变换,如何去构造想要的小波函数,然后还有离散小波变换,正交小波变换,二维小波变换,小波包的应用(这里没有介绍可以自己看资料)。好像还有很多要学习的。
这里先深入一下,父小波和母小波,多分辨率分析,了解一下伸缩和平移。
任何小波变换的基函数,其实就是对母小波和父小波缩放和平移的集合。首先要看的就是多分辨率分析。
每个小波变换都会有一个mother wavelet,我们称之为母小波,同时还有一个father wavelet,就是scaling function。而该小波的basis函数其实就是对这个母小波和父小波缩放和平移形成的。缩放倍数都是2的级数,平移的大小和当前其缩放的程度有关。
还讲到,小波系统有很多种,不同的母小波,衍生的小波基就完全不同。小波展开的近似形式是这样:
其中的就是小波级数,这些级数的组合就形成了小波变换中的基basis。和傅立叶级数有一点不同的是,小波级数通常是orthonormal basis,也就是说,它们不仅两两正交,还归一化了。
我们还讲了一般小波变换的三个特点,就是小波级数是二维的,能定位时域和频域,计算很快。但我们并没有深入讲解,比如,如何理解这个二维?它是如何同时定位频域和时域的?
在这一篇文章里,我们就来讨论一下这些特性背后的原理。
首先,我们一直都在讲小波展开的近似形式。那什么是完整形式呢?之前讲到,小波basis的形成,是基于基本的小波函数,也就是母小波来做缩放和平移的。但是,母小波并非唯一的原始基。在构建小波基函数集合的时候,通常还要用到一个函数叫尺度函数,scaling function,人们通常都称其为父小波。它和母小波一样,也是归一化了,而且它还需要满足一个性质,就是它和对自己本身周期平移的函数两两正交:
另外,为了方便处理,父小波和母小波也需要是正交的。可以说,完整的小波展开就是由母小波和父小波共同定义的。
其中ψ(t)是母小波,![]() 是父小波。需要提醒一点的是,这个正交纯粹是为了小波分析的方便而引入的特性,并不是说小波变换的基就一定必须是正交的。但大部分小波变换的基确实是正交的,所以本文就直接默认正交为小波变换的主要性质之一了。引入这个父小波呢,主要是为了方便做多解析度分析(multiresolution analysis, MRA)。说到这里,你的问题可能会井喷了:好好的为什么出来一个父小波呢?这个scaling function是拿来干嘛的?它背后的物理意义是什么?waveletfunction背后的物理意义又是什么?这个多解析度分析又是什么呢?不急,下面,我们围绕一个例子来巩固一下前面的知识,同时再引出新的特性。
是父小波。需要提醒一点的是,这个正交纯粹是为了小波分析的方便而引入的特性,并不是说小波变换的基就一定必须是正交的。但大部分小波变换的基确实是正交的,所以本文就直接默认正交为小波变换的主要性质之一了。引入这个父小波呢,主要是为了方便做多解析度分析(multiresolution analysis, MRA)。说到这里,你的问题可能会井喷了:好好的为什么出来一个父小波呢?这个scaling function是拿来干嘛的?它背后的物理意义是什么?waveletfunction背后的物理意义又是什么?这个多解析度分析又是什么呢?不急,下面,我们围绕一个例子来巩固一下前面的知识,同时再引出新的特性。
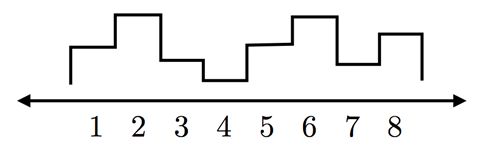
假设我们有这样一个信号:
该信号长度为8,是离散的一维信号。我们要考虑的,就是如何用小波将其展开。为了方便讲解,我们考虑最简单的一种小波,哈尔小波。下面是它的一种母小波:
那如何构建基于这个母小波的基呢?刚才提到了,要缩放,要平移。我们先试试缩放,那就是ψ(2n):
但这样的话,它与自己的内积就不是1了,不符合小波基orthonormal的要求,所以我们要在前面加一个系数根号二,这样我们就得到了另一个哈尔小波的basis function:
同理,我们可以一直这样推广下去做scale,得到4n,8n,…….下的basis function。当然在这个例子里,我们信号长度就是8,所以做到4n就够了。但推广来说,就是这种scaling对母小波的作用为![]() ,这是归一化后的表示形式。
,这是归一化后的表示形式。
平移的话也很简单,我们可以对母小波进行平移,也可以对scale之后的basis function进行平移。比如对上一幅图中的basis function进行平移,就成了
看得出来,平移后的basis function和母小波以及仅仅scale过的小波,都是正交的,附合小波basis的特点。如果我们用ψ(n)来表示这个mother wavelet,那么这些orthonormal basis函数可以写成:
![]()
这里的k是可以看成时域的参数,因为它控制着小波基时域的转移,而j是频域的参数,因为它决定了小波基的频率特性。看到这里,你应该会感觉很熟悉,因为这里的平移和变换本质和刚才对scaling function的平移变换是一模一样的。
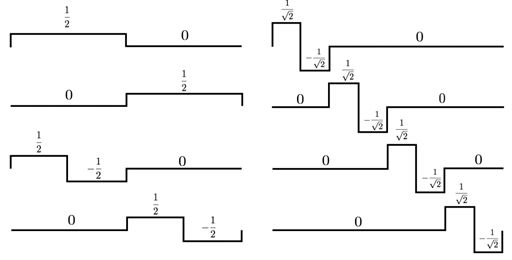
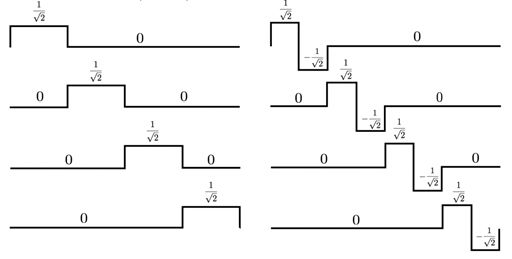
这样,我们就有了针对此信号space的哈尔小波basis组合:
可以看出,我们用到了三层频率尺度的小波函数,每往下一层,小波的数量都是上面一层的两倍。在图中,每一个小波基函数的表达形式都写在了波形的下面。
等等,你可能已经发现了,有问题。这里为什么多了个没有函数表达式的波形呢?这货明显不是wavelet function阿。没错,它是之前提到的scaling function,也就是父小波。然后你可能就会问,为啥这个凭空插了一个scaling function出来呢?明明目标信号已经可以用纯的小波基组合表示了。是,确实是,就算不包括scaling function,这些小波函数本身也组成了正交归一基,但如果仅限于此的话,小波变换也就没那么神奇的功效了。引入这个scaling function,才能引入我们提到的多解析度分析的理论,而小波变换的强大,就体现在这个多解析度上。那在这里,我们怎么用这个多解析度呢?这个哈尔小波basis组合是怎么通过多解析度推导出来的呢?
话说在数学定义中,有一种空间叫Lebesgue空间,对于信号处理非常重要,可以用L^p(R)表示,指的是由p次可积函数所组成的函数空间。我们在小波变换中要研究的信号都是属于L^2(R)空间的,这个空间是R上的所有处处平方可积的可测函数的集合,这样就等于对信号提出了一个限制,就是信号能量必须是有限的,否则它就不可积了。小波变换的定义都是基于但不限于L^2(R)中的信号的。这玩意的特性要具体解释起来太数学了,牵涉到太多泛函知识,我就不在这里详述了。而且老实说我也没能力完全讲清楚,毕竟不是学这个的,有兴趣可以参考wiki。总之你记住,小波变换研究中所使用的信号基本都是平方可积的信号,但其应用不限于这种信号,就行了。
对L^2(R)空间做MRA是在干嘛呢?就是说,在L^2(R)空间中,我们可以找出一个嵌套的空间序列,并有下列性质:
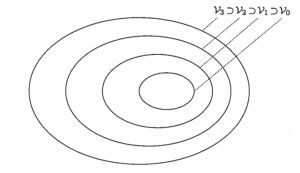
我来简单解释一下这些性质。这个V_j都是L^2(R)空间中的子空间,然后他们是由小到大的,交集是{0},因为这是最小的子空间,并集就是L空间。是不是有点难以理解?没关系,看看下面这个图就清楚了:
这个图是圈圈套圈圈,最里面的圈是V0,之后分别是V1,V2,V3,V4 。那他们有趣的性质就是,假如有一个函数f(t)他属于一个某空间,那你将其在时域上平移,它还是属于这个空间。但如果你对它频域的放大或缩小,它就会相应移到下一个或者上一个空间了。
同时我们还知道,你要形容每一个空间的话,都需要有对应的orthonormal basis,这是必然的,那对于V0来讲,它的orthonormal basis就是
这一系列函数是什么呢?是的时域变换,而且我们刚才也说了,时域上平移,是不会跳出这个空间的。这样,我们就可以说,由这一系列basis所定义的L^2(R)子空间V0被这些basis所span,表示成:
k从负无穷到正无穷。上面的bar表示这是一个闭包空间,也就是说
这样,我们就定义了基本的V0这个子空间。刚才说了,这个子空间的基都是对的整数时域变换,这里我们称为scalingfunction,所以换个说法,就是说这里整个子空间V0,由scalingfunction和其时域变换的兄弟们span。
当然,如果这个scaling function只是用来代表一个子空间的,那它的地位也就不会这么重要了。刚才我们提到,这个嵌套空间序列有一个性质,![]() 。这就是这个函数,如果你对它频域的放大或缩小,它就会相应移到下一个或者上一个空间了。这个性质就有意思了,它代表什么呢?对于任何一个包含V0的更上一层的空间来讲,他们的基都可以通过对scaling function做频域的scale后再做时域上的整数变换得到!推广开来就是说,当
。这就是这个函数,如果你对它频域的放大或缩小,它就会相应移到下一个或者上一个空间了。这个性质就有意思了,它代表什么呢?对于任何一个包含V0的更上一层的空间来讲,他们的基都可以通过对scaling function做频域的scale后再做时域上的整数变换得到!推广开来就是说,当
![]()
这也就意味着,对于任何属于V_j空间的函数f(t),都可以表示为:
到这里,我们就明白这些个子空间和那个凭空冒出来的scaling function的作用了。scaling的构建这些不同的子空间的基础,当j越大的时候,每一次你对频率变换后的scaling function所做的时域上的整数平移幅度会越小,这样在这个j子空间里面得到的f(t)表示粒度会很细,细节展现很多。反之亦然。通俗点说,就是对scaling function的变换平移给你不同的子空间,而不同的子空间给你不同的分辨率,这样你就可以用不同的分辨率去看目标信号。
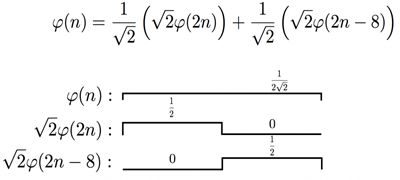
下面就是时候看看什么是MRA equation了,这是更加有趣,也是更加核心的地方。通过刚才的讲解,V0属于V1,那scaling function是在V0中的,自然也在V1中了。我们把他写成V1的基的线性组合,那就是
其中的h(n)是scaling function的系数,也叫做scaling filter或者scaling vector,可以是实数,也可以是虚数。根号2是为了维持norm为1的。看,在这个公式里,我们就把属于V0的函数用V1的基表示出来了。同理,我们可以循环如此,把属于V0的![]() 在V2,V3, …, Vn中表示出来。这些方程就是MRA equation,也叫refinement equation,它是scaling function理论的基础,也是小波分析的基础之一。
在V2,V3, …, Vn中表示出来。这些方程就是MRA equation,也叫refinement equation,它是scaling function理论的基础,也是小波分析的基础之一。
好,稍微总结一下。到现在,已经讲了关于scaling function的基本理论知识,知道了信号空间可以分为不同精细度的子空间,这些子空间的basis集合就是scaling function或者频率变换之后的scaling function,如下图所示:
上图就是四个子空间的basis集合的展览。通过前面的讨论,我们还知道,一开始的scalingfunction可以通过更精细的子空间的scaling function(它们都是对应子空间的basis)来构建。比如
对于更加finer的scale:
依此类推。实际上,对于任何scale和translate过的scaling function,都可以用更加精细的scale层面上的scaling function构建出来。
然后,我们有各种scale下的scaling function了,该看看它们分别所对应的嵌套的空间序列了。先看看V0,自然就是以基本的scaling function为基础去span出来的:
![]()
这个不新鲜,刚才就讲过了。这个子空间代表什么样的信号?常量信号。道理很简单,这个scaling function在整个信号长度上,没有任何变化。继续往下看:
![]()
这个相比V0更加finer的子空间,代表着这样一种信号,它从1-4是常量,从5-8是另一个常量。同理我们有:
V2代表的信号,是分别在1,2; 3,4; 5,6; 7,8上有相同值的信号。那么V3呢?则表示任何信号,因为对于V3来讲,任何一个时间刻度上的值都可以不一样。而且现在,我们也可以通过上面的一些scaling functions的波形验证了之前提到的多解析度分析中的一个核心性质,那就是:
![]()
我们之前讲了一堆多解析度的理论,但直到现在,通过这些图形化的分析,我们可能才会真正理解它。那好,既然我们有一个现成的信号,那就来看看,对这个信号作多解析度分析是啥样子的:
你看,在不同的子空间,对于同一个信号就有不同的诠释。诠释最好的当然是V3,完全不损失细节。这就是多解析度的意义。我们可以有嵌套的,由scalingfunction演变的basis function集合,每一个集合都提供对原始信号的某种近似,解析度越高,近似越精确。
说到这里,可能你对scaling function以及多解析度分析已经比较理解了。但是,我们还没有涉及到它们在小波变换中的具体应用,也就是还没有回答刚才那个问题:凭空插了一个scaling function到小波basis组合中干嘛。也就是说,我们希望理解scaling function是怎么和小波函数结合的呢,多解析度能给小波变换带来什么样的好处呢。这其实就是是小波变换中的核心知识。理解了这个,后面的小波变换就是纯数学计算了。
好,我们已经知道,对于子空间V0,basis是scalingfunction:
看出什么规律了么?多看几次这三个图,你会惊讶地发现,在V0中的scaling function和wavelet function的组合,其实就是V1中的basis!继续这样推导,V1本来的的basis是:
他们的组合,本质上也就是V2的basis(参考图2)。你继续推导下去,会得到同样的结论:在scale j的wavelet function,可以被用来将Vj的basis扩展到V(j+1)中去!这是一个非常非常关键的性质,因为这代表着,对任何一个子空间Vj,我们现在有两种方法去得到它的orthonormal basis:
1. 一种就是它本来的basis![]() ,对任意k。
,对任意k。
2. 第二种就是它上一个子空间的basis![]() ,对任意k,以及上一级子空间的wavelet function
,对任意k,以及上一级子空间的wavelet function ![]() ,对任意k。
,对任意k。
第二种选择能给我们带来额外的好处,那就是我们可以循环不断地用上一级子空间的scaling function以及wavelet function的组合来作为当前子空间的基。换句话说,如果针对V3这个子空间,它实际上就有四种不同的,但是等价的orthonormal basis:
1. 本级(V3)的scalingfunction basis set
2. 上一级(V2)的scalingfunction + wavelet function;
3 . 上上一级(V1)的scalingfunction + 上上一级(V1)的waveletfunction + 上一级(V2)的waveletfunction;
4. 上上上一级(V0)的scalingfunction + 上上上一级(V0)的waveletfunction + 上上一级(V1)的waveletfunction + 上一级(V2)的waveletfunction
好,看看最后一种选取方式,有没有感到眼熟?对了,它就是我们之前提到的“针对此信号space的哈尔小波basis组合”,参见图1。现在我们知道了,这个scalingfunction不是凭空插进去的,而是通过不断的嵌套迭代出来的:
那为什么我们最后选定的是这种选取方式呢?实际上,刚才介绍的这个性质已经告诉我们,对于任何的scale j0,我们都可以给我们的signal space找到一组orthonormal basis,这个basis是通过组合scale j0上的scaling function以及所有在scale j,j>=j0上的wavelets得到的。这样,基于这个orthonormal basis,
所有信号空间中的信号都可以写成组成这个basis的functions的线性组合:
对应的系数的计算和平常一样:
这,就是最终的,也是最核心的,小波变换形式。不管是信号压缩,滤波,还是别的方式处理,只要是用小波变换,都逃不出这个基础流程:
1. 选取合适的wavelet function和scaling function,从已有的信号中,反算出系数c和d。
2. 对系数做对应处理
3. 从处理后的系数中重新构建信号。
这里的系数处理是区别你的应用的重点。比如图像或者视频压缩,就希望选取能将能量聚集到很小一部分系数中的小波,然后抛弃那些能量很小的小波系数,只保留少数的这些大头系数,再反变换回去。这样的话,图像信号的能量并没有怎么丢失,图像体积却大大减小了。
还有一个没有解释的问题是,为什么要强调尺度函数和小波函数组成一个orthonormal basis呢?计算方便是一方面,还有一个原因是,如果他们满足这个性质,就满足瑞利能量定理,也就是说,信号的能量,可以完全用每个频域里面的展开部分的能量,也就是他们的展开系数表示:
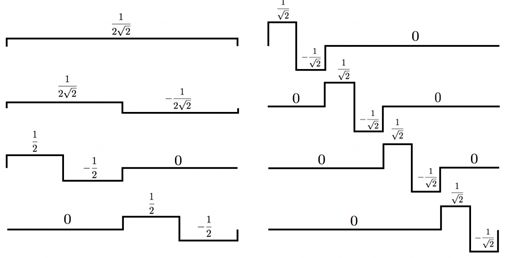
到这里,我们对小波变换的形式就讲完了。虽然是用的最简单的哈尔小波为例子,但举一反三即可。我们着重介绍了多解析度分析以及它给小波变换带来的杀手锏:时域频域同时定位。结束之前,再多说几句小波变换的意义。我们拿刚才例子中V3子空间的第二种可选择的orthonormal basis作为例子:
左边这四个basis组成元素,也就是scaling functions,的系数,表征的是信号的local平均(想想它们和信号的内积形式),而右边的这四个basis组成元素,也就是wavelet functions,的系数则表征了在local平均中丢失的信号细节。得益于此,多解析度分析能够对信号在越来越宽的区域上取平均,等同于做低通滤波,而且,它还能保留因为平均而损失的信号细节,等同于做高通滤波!这样,我们终于可以解释了wavelet function和scaling function背后的物理意义了:wavelet function等同于对信号做高通滤波保留变化细节,而scalingfunction等同于对信号做低通滤波保留平滑的shape!
对小波变换的基础知识,我们就讲到这里。需要注意的是,这只是小波变换最基本最基本的知识,但也是最核心的知识。看完这里其实就是回到了最开始的介绍:小波变换是把信号分解成一系列的小波(经过原始小波伸缩和平移得到的),这里就告诉了我们伸缩和平移
六、小波的应用
小波是多分辨率理论的分析基础。而多分辨率理论与多种分辨率下的信号表示和分析有关,其优势很明显--某种分辨率下无法发现的特性在另一个分辨率下将很容易被发现。从多分辨率的角度来审视小波变换,虽然解释小波变换的方式有很多,但这种方式能简化数学和物理的解释过程。
对于小波的应用很多,我学习的的方向主要是图像处理,所以这里用图像的应用来举例。对于图像,要知道量化级数决定了图像的分辨率,量化级数越高,图像越是清晰,图像的分辨率就高。
例一,哈尔小波图像分解
例二, 小波去噪平滑
例三, 小波的边缘检测
小波的知识还有很多,可以再继续看书学习,希望看到这个文章,可以对小波入门的同学有一定的帮助,下面给出几个不错的网站可以辅助学习
http://blog.163.com/renfengyuee@126/blog/static/35943136201091274316370/
http://www.zhihu.com/question/22864189
http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html
http://blog.csdn.net/wanglang3081/article/details/17751805