图-迪杰斯特拉（Dijkstra）算法详解（含全部代码）

目录

适用条件

基本操作函数

功能实现函数

 测试所用图

算法讲解

初始化结果

变化过程

迪杰斯特拉算法代码

 全部代码

实验结果

---

适用条件

图中不存在负权边。

基本操作函数

InitGraph(Graph &G)             初始化函数 参数：图G 作用：初始化图的顶点表，邻接矩阵等
InsertNode(Graph &G,VexType v) 插入点函数 参数：图G,顶点v 作用：在图G中插入顶点v,即改变顶点表
InsertEdge(Graph &G,VexType v,VexType w) 插入边函数 参数：图G,某边两端点v和w 作用：在图G两点v,w之间加入边，即改变邻接矩阵
Adjancent(Graph G,VexType v,VexType w) 判断是否存在边(v,w)函数 参数：图G，某边两端点v和w 作用：判断是否存在边(v,w)
BFS(Graph G, int start) 广度遍历函数 参数：图G,开始结点下标start 作用：宽度遍历
DFS(Graph G, int start) 深度遍历函数（递归形式）参数：图G,开始结点下标start 作用：深度遍历
Dijkstra(Graph G, int v)  最短路径 - Dijkstra算法 参数：图G、源点v

功能实现函数

CreateGraph(Graph &G) 创建图功能实现函数 参数：图G  InsertNode 作用：创建图
BFSTraverse(Graph G)  广度遍历功能实现函数 参数：图G 作用：宽度遍历
DFSTraverse(Graph G)  深度遍历功能实现函数 参数：图G 作用：深度遍历
Shortest_Dijkstra(Graph &G) 调用最短路径-Dijkstra算法 参数：图G、源点v

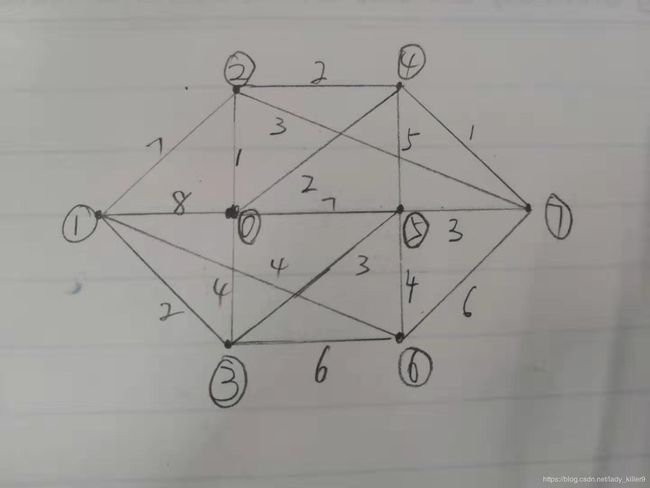
 测试所用图

测试用图

算法讲解

S:bool类型数组，加入最短路径的结果集，初始时只有源节点。

D:int类型数组，记录到图中各个节点的最短路径的值。

Pr:int类型数组，记录图中节点到源节点的前驱，在Path输出时递归即可输出最短路径。

初始化结果

以源节点为0节点做测试。

i	0	1	2	3	4	5	6	7
S[i]	true	false	false	false	false	false	false	false
D[i]	0	8	1	4	2	7	∞	∞
Pr[i]	-1	0	0	0	0	0	-1	-1

解释：初始化时，将源点加入S集合。哪些节点与源节点相连，则D的值就为其权值，其余为无穷大。与源节点相连，则前驱为源节点，其余的以-1取代，最终仅源节点的Pr值为-1，作为递归输出最短路径的出口。

变化过程

终点\轮数i	1	2	3	4	5	6	7
1	8	8	8
2	1
3	4	4	4
4	2	2
5	7	7	7
6	∞	∞	∞
7	∞	∞	3
Pr			Pr[7]=4
S	S[2]=true	S[4]=true	S[7]=true

解释：迪杰斯特拉采用贪心算法。首轮自然是选择与源点相连权值最小的节点2，将它加入集合，并且在加入节点2后进行更新。有人将这个更新过程称为松弛，就是比较其他节点在不通过新加入的节点到达源节点的路径长度与通过加入的新节点时到达源节点的路径长度哪一个更小，从而选择更小的。第二轮时没有更新，跳过。在第三轮时发现，源点到达节点7的路径长度为∞，在通过第2轮新加入的节点4时，路径长度变为2+1=3，这时发现恰好3为D集合中的最小值，则将节点7加入集合。请读者自行填好表格，并与最终结果进行比对以加深印象。

迪杰斯特拉算法代码

//最短路径 - Dijkstra算法 参数：图G、源点v
void Dijkstra(Graph G, int v)
{
	//初始化
	int n = G.vexnum;//n为图的顶点个数
	for (int i = 0; i < n; i++)
	{
		S[i] = false;
		D[i] = G.Edge[v][i];
		if (D[i] < INF)Pr[i] = v; //v与i连接，v为前驱
		else Pr[i] = -1;
	}
	S[v] = true;
	D[v] = 0;
	//初始化结束,求最短路径，并加入S集
	for (int i = 1; i < n; i++)
	{
		int min = INF;
		int temp;
		for (int w = 0; w < n; w++)
			if (!S[w] && D[w] < min) //某点temp未加入s集，且为当前最短路径
			{
				temp = w;
				min = D[w];
			}
		S[temp] = true;
	//更新从源点出发至其余点的最短路径 通过temp
		for (int w = 0; w < n; w++)
			if (!S[w] && D[temp] + G.Edge[temp][w] < D[w])
			{
				D[w] = D[temp] + G.Edge[temp][w];
				Pr[w] = temp;
			}
	}
}

 全部代码

/*
Project: 图-最短路径-Dijkstra算法
Date:    2019/10/16
Author:  Frank Yu
基本操作函数:
InitGraph(Graph &G)             初始化函数 参数：图G 作用：初始化图的顶点表，邻接矩阵等
InsertNode(Graph &G,VexType v) 插入点函数 参数：图G,顶点v 作用：在图G中插入顶点v,即改变顶点表
InsertEdge(Graph &G,VexType v,VexType w) 插入边函数 参数：图G,某边两端点v和w 作用：在图G两点v,w之间加入边，即改变邻接矩阵
Adjancent(Graph G,VexType v,VexType w) 判断是否存在边(v,w)函数 参数：图G，某边两端点v和w 作用：判断是否存在边(v,w)
BFS(Graph G, int start) 广度遍历函数 参数：图G,开始结点下标start 作用：宽度遍历
DFS(Graph G, int start) 深度遍历函数（递归形式）参数：图G,开始结点下标start 作用：深度遍历
Dijkstra(Graph G, int v)  最短路径 - Dijkstra算法 参数：图G、源点v
功能实现函数：
CreateGraph(Graph &G) 创建图功能实现函数 参数：图G  InsertNode 作用：创建图
BFSTraverse(Graph G)  广度遍历功能实现函数 参数：图G 作用：宽度遍历
DFSTraverse(Graph G)  深度遍历功能实现函数 参数：图G 作用：深度遍历
Shortest_Dijkstra(Graph &G) 调用最短路径-Dijkstra算法 参数：图G、源点v
*/
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

实验结果

实验数据：

8
17
0 1 2 3 4 5 6 7
0 1 8
0 2 1
0 3 4
0 4 2
0 5 7
1 2 7
1 3 2
1 6 4
2 4 2
2 7 3
3 5 3
3 6 6
4 5 5
4 7 1
5 6 4
5 7 3
6 7 6

最短路径：

红笔标注最短路径

 最短路径形成的树：

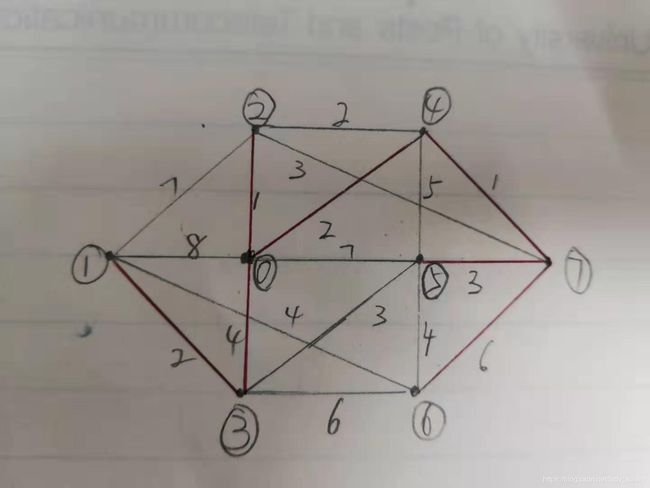
对应最短路径形成的树

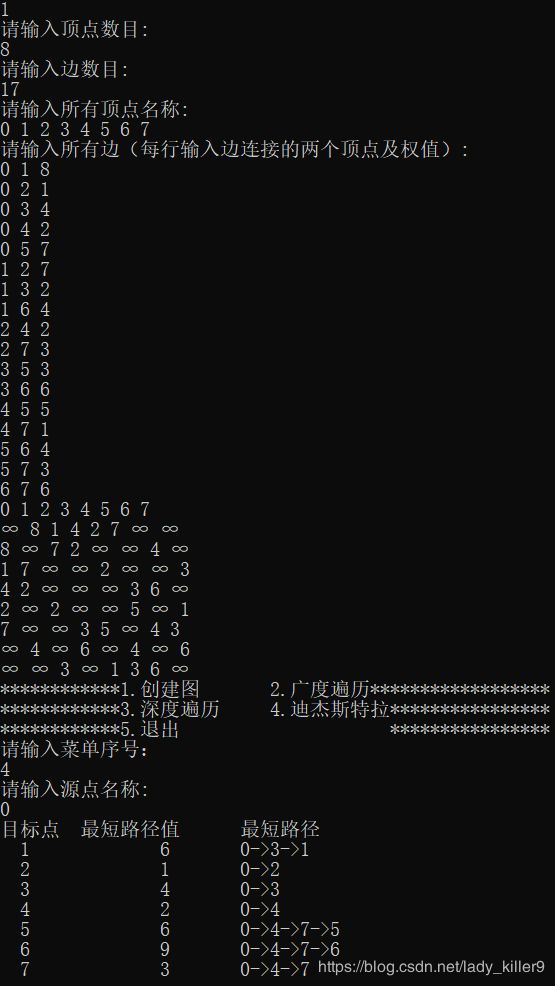
实验结果截图：

结果截图

在代码中，求出了一个节点到其他所有节点的最短路径，如果只是一对一，也就是一个节点到一个节点的最短路径呢？此时，只需要修改代码，，加入一个条件语句在得到目标节点的最短路径时停止即可。同样，求出所有节点作为源节点，到其他所有节点的最短路径时，只需要现有程序外部再加一个for循环，遍历所有节点做源节点即可。

更多数据结构与算法实现：数据结构（严蔚敏版）与算法的实现（含全部代码）

有问题请下方评论，转载请注明出处，并附有原文链接，谢谢！如有侵权，请及时联系。