Kernel Trick——核机制,更高维空间内积的快速计算
这是小弟的第一篇技术博客,功力尚浅,写的不准确不专业的地方,还请各位同仁,多多包涵。
blog归正传。
-
- 引言
- 理论
- 1 Kernel SVM
- 2 2阶多项式核
- 3 常见核的种类
- 应用
- 1 Kernel SVM
- 2 Kernel PCA
- 3 核密度估计KDE
1. 引言
Kernel是什么,几乎没有一本机器学习或模式识别的书,Kernel思想及应用不是贯穿全书,也就是说Kernel思想刷新了模式识别的许多经典算法(下面会说到,只要涉及空间的变换、涉及内积的运算,都是Kernel大展身手的舞台)。
不卖关子,如title所说,核机制:更高维空间内积的快速计算。也就是说,核机制的本质是计算内积(只不过这里参与内积运算的两点属于更高维的空间)。
如果数据在当前空间中不是线性可分的,则需做transform,将数据变换到更高的维度空间中。
也就是:
Kernel = transform + inner product
Kernel机制的必要性和有效性可通过对比传统的高维空间计算内积的方法显现。
传统的方法要分两步,
- step1: 先从 X 空间升维到 Z 空间。
ϕ(x):X→Z
一般情况下, Z 空间具有更高的维度。如果升维到无穷维空间,计算量更是难以忍受。 - step2: 再在 Z 空间里计算内积
zT1z2
核的方法:
也就是说, K(x1,x2) 计算得到的结果就是原始数据空间里的两点先升维 ϕ(x) 再进行内积 ϕ(x1)Tϕ(x2) 的结果,不必通过显式的升维变换,也即是说, K(⋅) 本身内嵌(embedded)了一种升维变换。两步变一步,形式更为简洁,具体如何降低运算量的,可通过part 2说明。
2. 理论
一切从SVM对偶问题的标准型说起。
2.1 Kernel SVM
核机制真正进入人们的视野是用作为简化SVM最优化问题的工具(kernel trick)提出。我们来看SVM的对偶问题:
使用Kernel Trick替换原有的内积运算:
根据KKT条件:
又有
取一个不为0的 αn (也即Support Vector,SV),可得:
知SVM解分类问题的分类决策函数为:
便不需要再显式的求解 ω 。
这样从计算拉格朗日乘子 α ,到得到分类函数的bias b∗ ,再到获得最终的分类决策函数,完全避开了更高维空间的内积运算,与高维空间的维度无关,只有当前数据空间的维度 d 有关。这样也简略地获悉Kernel机制的使用范围,也即较大的数据量 N ,较小的维度 d 。
2.2 2阶多项式核
现在我们来考察,核机制是如何不经历升维变换便可直接计算对应高维空间的内积的。
我们以二阶多项式核变换为例(假设原始数据属于 Rd 空间):
出于简洁性的考虑,我们将 xnxm & xmxn 都包括在内。
如此一来, O(d2) 的时间复杂度就降低到 O(d) ,也就是说kernel机制的
计算与变换域的维度无关( d2 代表二阶多项式变换下的空间维度)。
同理可类推更为一般的二阶多项式核。
2.3 常见核的种类
- 多项式核函数(Polynomial kernel function)
K(x1,x2)=(xT1x2+1)p
对应的支持向量机是一个 p 此多项式分类器,在此情形下,分类决策函数为
g(x)=sign(∑n=1Nα∗nyn(xTnx+1)p+b∗) - 高斯核函数(Gaussian kernel function)
K(x1,x2)=exp(−∥x1−x2∥2σ2)
对应的支持向量机是高斯径向基函数(RBF,Radial basis function)分类器,在此情形下,分类决策函数称为:
g(x)=sign(∑n=1Nα∗nynexp(−∥xn−x∥2σ2)+b∗)
3. 应用
从理论到应用,不可逾越的鸿沟还是一层窗户纸?
这里不妨扯个闲篇,或者我站着说话不腰疼,为什么从数学家们推导出来的理论到实现出来,其实只隔着一层窗户纸呢?这里只举一例,压缩感知,压缩过程(compressing phase)的实现,只需对原始矩阵左乘一个 Φ 矩阵,当然这里的 Φ 需要满足一定的性质,具体哪些性质、这些性质怎么来的,这是数学家们的工作。如果不对理论进行更多的探索,而是直接使用现成的结论的话,从原始的数据域转换 P 到压缩域 X ,只需简单的一步(RP,random projection):
如何从压缩域(也就是观测数据)以高概率重构出原始数据,就是另外的话题了,这也是压缩感知关注的唯二的重点。
3.1 Kernel SVM
本文的主角是Kernel机制,而不是如何解SVM优化问题。为了说明问题,这里采用最为原始的二次规划(solver:Quadratic Programming,QP)解SVM问题,并将高斯核函数应用其中。
在写代码之前,先考虑如何将原始SVM对偶问题适配(adapt)matlab QP二次规划工具箱函数。
原始SVM对偶问题:
matlab QP二次规划函数接口:
对应的二次规划问题:
依样画葫芦,可对原始SVM形式做如下的改造:
x=α
H=(ynymK(xn,xm))N⋅N
c=−1Td
A=−IN⋅N
b=0d
Aeq=yT
beq=0
- 生成线性不可分的training data
%% training set
rng('default');
N = 150;
X = 10*rand(150, 2)-5;
y = zeros(N, 1)-1;
y((X(:, 1).^3+X(:, 1).^2+X(:, 1)+1)/20>X(:, 2)) = 1;
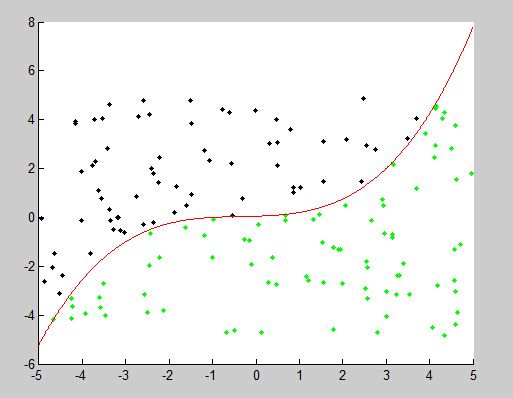
- 数据可视化(visualization)
scatter(X(y==-1, 1), X(y==-1, 2), 'k.'), hold on
scatter(X(y==1, 1), X(y==1, 2), 'g.'),
t = -5:.01:5;
plot(t, (t.^3+t.^2+t+1)/20, 'r' ),
数据服从[-5, 5]的二维平均分布,分类线为 y=(x3+x2+x+1)/20 。
- 生层测试样本(test data)
N2 = 200;
X2 = 10*rand(N2, 2) - 5;
y2 = zeros(N2, 1) - 1;
y2((X2(:, 1).^3+X2(:, 1).^2+X2(:, 1)+1)/20 > X2(:, 2)) = 1;- 计算高斯核 K 矩阵(这一步便是所说的从理论到实践的一层窗户纸)
sigma = 3;
K = zeros(N, N);
for i = 1:N,
for j = i:N,
t = X(i, :)-X(j, :);
K(i, j) = exp(-(t*t')/sigma^2);
K(j, i) = K(i, j);
end
end- 适配对应QP函数的参数
H = (y*y').*K;
f = -ones(N, 1);
A = -eye(N); b = zeros(N, 1);
Aeq = y'; beq = 0;- 计算 α 和 b∗
alpha = quadprog(H, f, A, b, Aeq, beq);
idx = find(abs(alpha) > 1e-4); # 画出支持向量
plot(X(idx, 1), X(idx, 2), 'ro')
b = y(idx(1)) - (alpha.*y)'*K(:, idx(1));- 机器学习的prediction phase
K2 = zeros(N, N2);
for i = 1:N2,
t = sum((X - (X2(i, :)'*ones(1, N))').^2, 2);
K2(:, i) = exp(-(t)/sigma^2);
end
y_pred = sign( (alpha.*y)'*K2 + b)';
sum(y2==y_pred)/N2 #计算精确度 0.9850注意,当高斯核函数唯一的参数 σ 取不同的值( σ=0.1 , σ=2 )时,会较大程度的影响最后的分类精确。