EAST文本检测与Keras实现
1. 引言
之前介绍了文本检测中的CTPN方法,详情可参见《CTPN文本检测与tensorflow实现》,虽然该方法在水平文本的检测方面效果比较好,但是对于竖直文本或者倾斜的文本,该方法的检测就很差,因此,在该方法之后,很多学者也提出了各种改进方法,其中,有一篇比较经典的就是旷世科技在2017年提出来的EAST模型,论文的全称为《EAST: An Efficient and Accurate Scene Text Detector》,论文的下载地址如下:
- 论文地址:https://arxiv.org/pdf/1704.03155.pdf
本文将对该方法进行具体介绍,并利用Keras对其进行复现。
2.EAST模型介绍
2.1 EAST模型结构
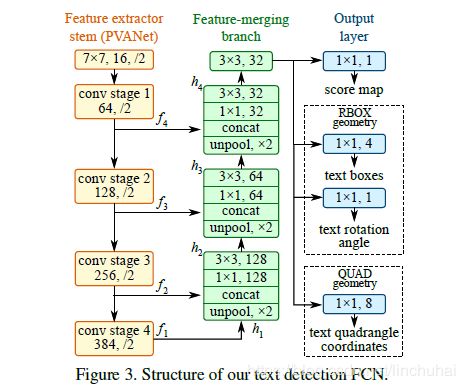
EAST的网络结构总共包含三个部分:feature extractor stem(特征提取分支), feature-merging branch(特征合并分支) 以及 output layer(输出层)。
在特征提取分支部分,主要由四层卷积层组成,可以是一些预训练好的卷积层,作者采用的是VGG16中pooling-2到pooling-5每一层得到的feature map。记每一层卷积层卷积后得到feature map为![]() ,如图1所示,从上到下唉,每一层feature map对应的尺度刚好为输入图像的
,如图1所示,从上到下唉,每一层feature map对应的尺度刚好为输入图像的![]() 。
。
在特征合并分支部分,其实作者借鉴了U-net的思想,只是U-net采用的是反卷积的操作,而这里采用的是反池化的操作,具体的计算大致如下,对于一个![]() ,首先经过一层反池化操作,得到与上一层卷积feature map同样大小的特征,然后将其与
,首先经过一层反池化操作,得到与上一层卷积feature map同样大小的特征,然后将其与![]() 进行拼接,拼接后再依次进入一层
进行拼接,拼接后再依次进入一层![]() 和
和![]() 的卷积层,以减少拼接后通道数的增加,得到对应的
的卷积层,以减少拼接后通道数的增加,得到对应的![]() ,在特征合并分支的最后一层,是一层
,在特征合并分支的最后一层,是一层![]() 的卷积层,卷积后得到的feature map最终直接进入输出层。具体的计算公式如下:
的卷积层,卷积后得到的feature map最终直接进入输出层。具体的计算公式如下:
其中,![]() 被称为合并基,
被称为合并基,![]() 是合并后得到feature map,
是合并后得到feature map,![]() 表示连接操作。之所以要引入特征合并分支,是因为在场景文字识别中,文字的大小非常极端,较大的文字需要神经网络高层的特征信息,而比较小的文字则需要神经网络浅层的特征信息,因此,只有将网络不同层次的特征进行融合才能满足这样的需求。
表示连接操作。之所以要引入特征合并分支,是因为在场景文字识别中,文字的大小非常极端,较大的文字需要神经网络高层的特征信息,而比较小的文字则需要神经网络浅层的特征信息,因此,只有将网络不同层次的特征进行融合才能满足这样的需求。
在输出层部分,主要有两部分,一部分是用单个通道的![]() 卷积得到score map(分数图),记为
卷积得到score map(分数图),记为![]() ,另一部分是多个通道的
,另一部分是多个通道的![]() 卷积得到geometry map(几何形状图),记为
卷积得到geometry map(几何形状图),记为![]() ,在这一部分,几何形状可以是RBOX(旋转盒子)或者QUAD(四边形)。对于RBOX,主要有5个通道,其中四个通道表示每一个像素点与文本线上、右、下、左边界距离(axis-aligned bounding box,AABB),记为
,在这一部分,几何形状可以是RBOX(旋转盒子)或者QUAD(四边形)。对于RBOX,主要有5个通道,其中四个通道表示每一个像素点与文本线上、右、下、左边界距离(axis-aligned bounding box,AABB),记为![]() ,另一个通道表示该四边形的旋转角度
,另一个通道表示该四边形的旋转角度![]() 。对于QUAD,则采用四边形四个顶点的坐标表示,每个点的坐标为
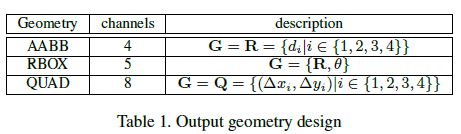
。对于QUAD,则采用四边形四个顶点的坐标表示,每个点的坐标为![]() ,因此,总共有8个通道。关于RBOX和QUAD的表示可以见表1:
,因此,总共有8个通道。关于RBOX和QUAD的表示可以见表1:
2.2 真实标签生成
对于score map,不失一般性的,这里考虑QUAD的情况,在RBOX也似类似的标签生成方式。EAST对真实标签的四边形区域会进行放缩,放缩的方式如下:
首先,记四边形![]() ,其中,
,其中,![]() 表示四边形顺时针方向的四个顶点,然后计算每个顶点
表示四边形顺时针方向的四个顶点,然后计算每个顶点![]() 的参考长度
的参考长度![]() ,说简单一点,其实就是计算每个顶点相邻两条边的最短边的长度,其计算公式如下:
,说简单一点,其实就是计算每个顶点相邻两条边的最短边的长度,其计算公式如下:
其中,![]() 表示
表示![]() 和
和![]() 的欧式距离。
的欧式距离。
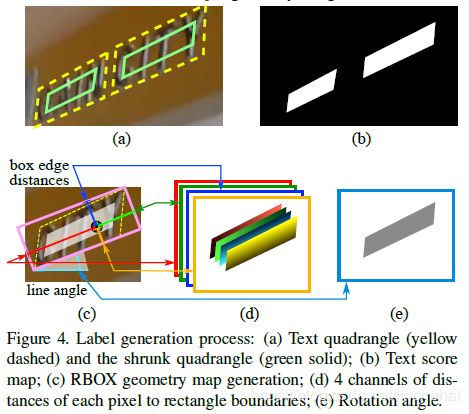
接着,对于四边形每一对对边,将两条边的长度与他们的均值进行对比,以确定出哪对对边是长边,然后对两条长边优先进行放缩,放缩的方式是对每个顶点沿着边向内部分别移动0.3![]() ,如图2(a)所示。
,如图2(a)所示。
对于geometry map,由前面我们知道有两种类型,分别是QUAD和RBOX,对于score map为正例的像素点,其QUAD对应的标签直接是他们与四个顶点的偏移坐标,即顶点的差值,而对于RBOX,则首先会选择一个最小的矩形框住真实的四边形,然后计算每个正例像素点与该矩形四条边界的距离。具体的如图2(c)-(e)所示。
2.3 损失函数
由于输出层有两个分支,因此对应着两个损失函数,可以表达如下:
![]()
其中,![]() 和
和![]() 分别表示score map和geometry map的损失函数,
分别表示score map和geometry map的损失函数,![]() 表示权重,在论文中作者设置为1。
表示权重,在论文中作者设置为1。
对于![]() ,为了解决类别不平衡的问题,作者引入了平衡交叉熵损失函数,其表达形式如下:
,为了解决类别不平衡的问题,作者引入了平衡交叉熵损失函数,其表达形式如下:
其中,![]() 是预测出来的分数,
是预测出来的分数,![]() 是真实的标签,
是真实的标签,![]() 是每一张图像中负例的占比,其计算公式如下:
是每一张图像中负例的占比,其计算公式如下:
对于![]() ,当geometry map采用的是RBOX时,对于RBOX中的AABB,作者采用的是
,当geometry map采用的是RBOX时,对于RBOX中的AABB,作者采用的是![]() 损失函数,其表达形式如下:
损失函数,其表达形式如下:
其中,![]() 表示预测到的矩形,
表示预测到的矩形,![]() 表示真实的矩形,
表示真实的矩形,![]() 表示两个矩形的重叠面积,其对应的宽和高计算方式如下:
表示两个矩形的重叠面积,其对应的宽和高计算方式如下:
其中,![]() 分别代表一个像素点到矩形上、右、下、左边界的距离,
分别代表一个像素点到矩形上、右、下、左边界的距离,![]() 表示两个矩形的总区域,其计算公式如下:
表示两个矩形的总区域,其计算公式如下:
由于RBOX还有一个通道是表示旋转角度,因此,对于角度的损失函数计算如下:
其中,![]() 表示预测到的角度,
表示预测到的角度,![]() 是真实的角度,最后,RBOX的损失函数如下:
是真实的角度,最后,RBOX的损失函数如下:
![]()
其中,![]() 表示权重,作者在实验时取的是10。
表示权重,作者在实验时取的是10。
对于![]() ,当geometry map采用的是QUAD时,此时损失函数的计算方式与RBOX不一样,作者采用的是smoothed-L1损失函数。记一个四边形Q对应的坐标集合为
,当geometry map采用的是QUAD时,此时损失函数的计算方式与RBOX不一样,作者采用的是smoothed-L1损失函数。记一个四边形Q对应的坐标集合为![]() ,则QUAD对应的损失函数如下:
,则QUAD对应的损失函数如下:
其中,![]() ,表示每个四边形的最小边长,而
,表示每个四边形的最小边长,而![]() 是与
是与![]() 等价的四边形集合,唯一的不同就是
等价的四边形集合,唯一的不同就是![]() 是经过排序,因为原始数据中,
是经过排序,因为原始数据中,![]() 的标注是无序的。
的标注是无序的。
2.4 局部感知NMS
当预测结束后,需要对文本线进行构造,为了提高构造的速度,作者提出了一种局部感知NMS算法,其基本思想是假设相邻的像素点之间是高度相关的,然后按行逐渐合并几何形状,当相邻两个几何形状满足合并条件(这里的合并条件作者没有具体讲清楚)时,对他们的坐标按照分数进行加权,其计算公式如下:
![]()
![]()
![]()
其中,![]() 分别表示两个满足合并的几何形状,
分别表示两个满足合并的几何形状,![]() 分别表示他们的分数,
分别表示他们的分数,![]() 分别对应第i个坐标,
分别对应第i个坐标,![]() 分别对应合并后的坐标和分数,当合并完成后,会将合并后的几何形状作为一个整体继续合并下去,直到不满足合并条件,将此时合并后的几何形状作为一个文本线保存到
分别对应合并后的坐标和分数,当合并完成后,会将合并后的几何形状作为一个整体继续合并下去,直到不满足合并条件,将此时合并后的几何形状作为一个文本线保存到![]() 当中,重复该过程,直到所有的几何形状都遍历一遍为止。具体的算法过程如下图:
当中,重复该过程,直到所有的几何形状都遍历一遍为止。具体的算法过程如下图:
3.Keras实现
本文利用Keras框架进行复现,主要参考的是huoyijie的代码,原始代码链接如下:
- 参考代码链接:https://github.com/huoyijie/AdvancedEAST
由于原始的EAST模型是对文本线内的每一个像素点的坐标进行预测,然后对其按照score进行加权平均,作为最终文本线的预测坐标,但是这种方法会有一个缺点,也就是容易导致文本线的坐标容易受到内部像素点的影响,导致预测的文本线偏小,没法准确地框住完整的文本,如下图所示:
因此,huoyijie对其进行了改进,他的改进思想是既然对文本线内的所有像素点的坐标进行预测比较难,那就只对文本线的边界点进行预测,然后只对边界点的坐标进行加权平均,这样就可以加快模型的收敛速度和精度,如下图所示,是他改进方法之后的效果,其中黄色和绿色点就是边界点。
这种想法确实是挺妙的,不得不佩服大佬,不过这种方法虽然提高了对文本检测的精度,但是在构建文本线时确有问题,当对边界点的预测不准确时,比如漏了左侧边界或者右侧边界时,就会导致整个文本线都构造失败,因此,反而使得模型的预测效果更差。
因此,笔者对代码中的文本线构造方法进行修改,笔者的思想是既然采用边界预测可以使得对文本的打点更加准确,那可以直接根据这些像素点的分布,用一个矩形框把它们直接框起来,那这样计算漏掉了某一测或全部的边界点,文本线也可以构建成功,但是这种方法也有一个不好的地方就是对于倾斜的文本,只能用矩形框住,而没法用随意的四边形框住。笔者在作者原来代码的基础上进行小部分修改后,主要修改的代码如下:
def nms(predict, activation_pixels, threshold=cfg.side_vertex_pixel_threshold):
region_list = []
for i, j in zip(activation_pixels[0], activation_pixels[1]):
merge = False
for k in range(len(region_list)):
if should_merge(region_list[k], i, j):
region_list[k].add((i, j))
merge = True
# Fixme 重叠文本区域处理,存在和多个区域邻接的pixels,先都merge试试
# break
if not merge:
region_list.append({(i, j)})
D = region_group(region_list)
quad_list = np.zeros((len(D), 4, 2))
score_list = np.zeros((len(D), 4))
# TODO(linchuhai):这里确定每个文本框的坐标还需要进一步修改
for group, g_th in zip(D, range(len(D))):
cord_list = []
for row in group:
for ij in region_list[row]:
cord_list.append((ij[0], ij[1]))
cord_list = np.array(cord_list)
min_i, min_j = np.amin(cord_list, axis=0)
max_i, max_j = np.amax(cord_list, axis=0)
quad_list[g_th, 0] = np.array([(min_j - 1) * cfg.pixel_size, (min_i - 1) * cfg.pixel_size])
quad_list[g_th, 1] = np.array([(min_j - 1) * cfg.pixel_size, (max_i + 1) * cfg.pixel_size])
quad_list[g_th, 2] = np.array([(max_j + 1) * cfg.pixel_size, (max_i + 1) * cfg.pixel_size])
quad_list[g_th, 3] = np.array([(max_j + 1) * cfg.pixel_size, (min_i - 1) * cfg.pixel_size])
return score_list, quad_list另外,huoyijie的代码里面还有一个小错误,就是对文本线进行放缩时,放缩的顺序弄错了,修改的地方如下:
# cal r length array
# r = [np.minimum(dis[i], dis[(i + 1) % 4]) for i in range(4)]
r = [np.minimum(dis[3], dis[(3 + 1) % 4])]
for i in range(3):
r.append(np.minimum(dis[i], dis[(i + 1) % 4]))因为参考代码已经写的比较完善,所以这次没有对代码进行大幅度修改,就不贴出模型其他部分的代码了。最后,模型的效果如下:
4.优缺点总结
最后,还是谈一下对EAST模型的一些看法吧,首先是优点:
- 结构简单,pipeline短,模型训练和预测的速度快
- 可以适用于单词或文本行级别的文本检测,并且文本框的形状可以是任意四边形,对竖直、倾斜文本的检测效果要比CTPN好
- 模型采用全卷积神经网络,参数量更加轻量级,并且速度也更快
接着是缺点部分,EAST模型的缺点主要有:
- 对长文本的检测不够准确
- 模型的感受野有限,当遇到一些比较大的文字时,可能就没法识别出来
不过总而言之,还是很钦佩旷世科技,最近旷世科技又提出了一个新模型,叫SPCnet,可以支持对弯曲文字的检测, 后面有时间再好好拜读一下。