GPT原理介绍
1.引言
前面我们介绍了ELMo算法的思想,通过在大量的语料上预训练语言模型,然后再将预训练好的模型迁移到具体的下游NLP任务,从而提高模型的能力。但是ELMo预训练的语言模型结构和下游的NLP任务的模型经常会不一致,因此,做迁移学习时经常没法将两者的模型直接进行融合,因此,本文将介绍OpenAI在2018年提出来的一个方法——GPT,该模型在预训练语言模型的基础上,只需要做一些微改即可直接迁移到各种NLP任务中,因此,其迁移能力更强。
- 论文地址:《Improving Language Understanding by Generative Pre-Training》
2.GPT原理介绍
GPT模型主要包含两个阶段,第一个阶段,先利用大量未标注的语料预训练一个语言模型,接着,在第二个阶段对预训练好的语言模型进行微改,将其迁移到各种有监督的NLP任务,并对参数进行fine-tuning。
2.1 预训练模型(无监督)
给定一个没有标注的大语料,记每一个序列为 U = { u 1 , … , u n } \mathcal{U}=\left\{u_{1}, \dots, u_{n}\right\} U={u1,…,un},GPT通过最大化以下似然函数来训练语言模型:
L 1 ( U ) = ∑ i log P ( u i ∣ u i − k , … , u i − 1 ; Θ ) L_{1}(\mathcal{U})=\sum_{i} \log P\left(u_{i} | u_{i-k}, \ldots, u_{i-1} ; \Theta\right) L1(U)=i∑logP(ui∣ui−k,…,ui−1;Θ)
其中, k k k表示上下文窗口的大小,这里计算每个单词的预测概率时,只考虑左侧窗口大小的词汇信息,在GPT中,作者采用的是一个12层的Transformer decoder作为语言模型的结构,其计算过程如下:
h 0 = U W e + W p h l = transformer_block ( h l − 1 ) ∀ i ∈ [ 1 , n ] P ( u ) = softmax ( h n W e T ) \begin{aligned} h_{0} &=U W_{e}+W_{p} \\ h_{l} &=\text { transformer\_block }\left(h_{l-1}\right) \forall i \in[1, n] \\ P(u) &=\operatorname{softmax}\left(h_{n} W_{e}^{T}\right) \end{aligned} h0hlP(u)=UWe+Wp= transformer_block (hl−1)∀i∈[1,n]=softmax(hnWeT)
其中, U = ( u − k , … , u − 1 ) U=\left(u_{-k}, \ldots, u_{-1}\right) U=(u−k,…,u−1)表示左侧窗口的词汇向量, n n n表示Transformer的层数, W e W_{e} We表示词向量矩阵, W p W_{p} Wp表示position embedding矩阵,在GPT中,作者对position embedding矩阵进行随机初始化,并让模型自己学习,而不是采用正弦余弦函数进行计算。
从GPT的计算公式来看,其实跟Transformer基本是一样的,只是对每个时间步,都只考虑左侧窗口大小的上下文信息。
2.2 fine-tuning(有监督)
当语言模型训练结束后,就可以将其迁移到具体的NLP任务中,假设将其迁移到一个文本分类任务中,记此时的数据集为 C \mathcal{C} C,对于每一个样本,其输入为 x 1 , … , x m x^{1}, \ldots, x^{m} x1,…,xm,输出为 y y y。对于每一个输入,经过预训练后的语言模型后,可以直接选取最后一层Transformer最后一个时间步的输出向量 h l m h_{l}^{m} hlm,然后在其后面接一层全连接层,即可得到最后的预测标签概率:
P ( y ∣ x 1 , … , x m ) = softmax ( h l m W y ) P\left(y | x^{1}, \ldots, x^{m}\right)=\operatorname{softmax}\left(h_{l}^{m} W_{y}\right) P(y∣x1,…,xm)=softmax(hlmWy)
其中, W y W_{y} Wy为新引入的全连接层的参数矩阵。因此,可以得到在分类任务中的目标函数:
L 2 ( C ) = ∑ ( x , y ) log P ( y ∣ x 1 , … , x m ) L_{2}(\mathcal{C})=\sum_{(x, y)} \log P\left(y | x^{1}, \ldots, x^{m}\right) L2(C)=(x,y)∑logP(y∣x1,…,xm)
在具体的NLP任务中,作者在fine-tuning时也把语言模型的目标引入到目标函数中,作为辅助函数,作者发现这样操作可以提高模型的通用能力,并且加速模型收敛,其形式如下:
L 3 ( C ) = L 2 ( C ) + λ ∗ L 1 ( C ) L_{3}(\mathcal{C})=L_{2}(\mathcal{C})+\lambda * L_{1}(\mathcal{C}) L3(C)=L2(C)+λ∗L1(C) 其中, λ \lambda λ一般取0.5。
可以发现,在fine-tuning阶段,此时新增的参数只有最后一层全连接层的参数 W y W_{y} Wy,这比ELMo算法要容易得多。
不过,上面这个例子只是对于文本分类任务,如果是对于其他任务,比如文本蕴涵、问答、文本相似度等,那么GPT该如何进行微改呢?针对这几种情况,作者提出了以下的修改方法:
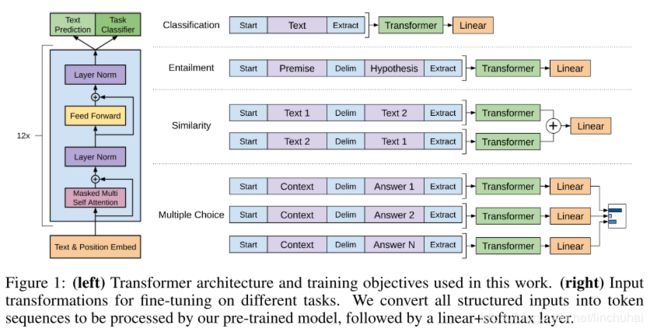
- 文本蕴涵:对于文本蕴涵任务,作者用一个“$”符号将文本和假设进行拼接,并在拼接后的文本前后加入开始符“start”和结束符“end”,然后将拼接后的文本直接传入预训练的语言模型,在模型再接一层线性变换和softmax即可。
- 文本相似度:对于文本相似度任务,由于相似度不需要考虑两个句子的顺序关系,因此,为了反映这一点,作者将两个句子分别与另一个句子进行拼接,中间用“$”进行隔开,并且前后还是加上起始和结束符,然后分别将拼接后的两个长句子传入Transformer,最后分别得到两个句子的向量表示 h l m h_{l}^{m} hlm,将这两个向量进行元素相加,然后再接如线性层和softmax层。
- 问答和常识推理:对于问答和常识推理任务,首先将背景信息与问题进行拼接,然后再将拼接后的文本依次与每个答案进行拼接,最后依次传入Transformer模型,最后接一层线性层得多每个输入的预测值。
具体的方法可以查看下图,可以发现,对这些任务的微改主要是新增线性层的参数以及起始符、结束符和分隔符三种特殊符号的向量参数。
3.总结
最后总结一下:
- GPT其实跟ELMO非常相似,只是把语言模型直接迁移到具体的NLP任务中,因此,更容易进行迁移学习。
- 不过GPT主要还是针对文本分类和标注性任务,如果对于生成任务,比如机器翻译等,则其结构也没法进行很好的迁移。