TensFlow深度学习(RNN)实现MNIST手写图片识别

1、DNN

https://blog.csdn.net/lingzw2011/article/details/82225399

2、CNN

https://blog.csdn.net/lingzw2011/article/details/85229561

3、RNN

RNN（循环神经网路）是一种特殊的神经网络结构，它是根据“人的认知是基于过往的经验和记忆”这一观点提出的；它与DNN、CNN不同的是：它不仅考虑前一时刻的输入，而且赋予了网络对前面的内容的一种“记忆”功能，即一个序列当前的输出与前面的输出也有关。
RNN具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。

RNN的应用领域：
① 自然语言处理(NLP): 主要有视频处理, 文本生成, 语言模型, 图像处理
② 机器翻译, 机器写小说
③ 语音识别
④ 图像描述生成
⑤ 文本相似度计算
⑥ 音乐推荐、网易考拉商品推荐、Youtube视频推荐等新的应用领域

4、RNN模型结构

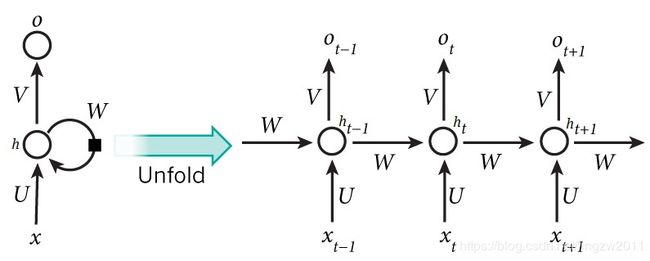
X是输入序列向量，h代表网络隐藏层的状态，O代表输出向量，输入层与隐藏层之间通过参数矩阵U连接，不同时刻的隐藏层之间通过参数矩阵W连接，隐藏层与输出层通过参数矩阵V连接， 权重参数（U、V、W）是共享的，如下图直观表达：

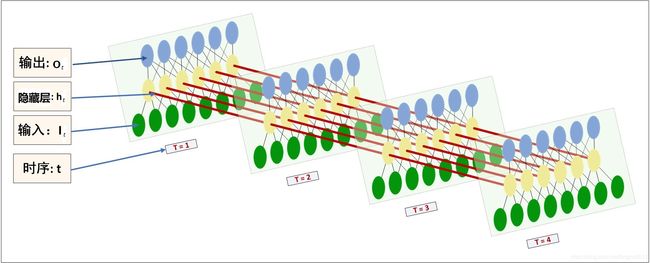
4.1 前向传播公式：

h_t = f (Wh_t-1 + Ux_t +b₁)

O_t = Vh_t + b₂

y_t = g (O_t)

其中 f 和 g 均为激活函数，f 可以是tanh、relu、sigmoid等激活函数，g 通常是softmax函数；X_t代表t时刻的输入，h_t代表t时刻的隐藏层状态，O_t代表t时刻的输出，y_t代表经过归一化后的预测概率。

4.2 根据输入和输出的不同，RNN在应用中有如下一些形态：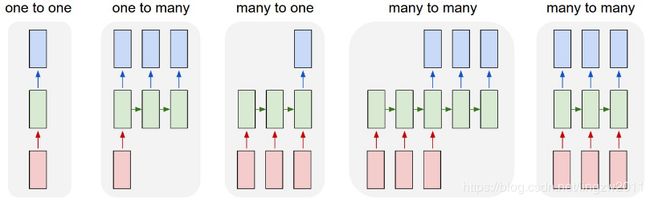
One to one : 传统文本分类
One to many: 英文释义
Many to one: 情感分析
Many to many: 机器翻译
Many to many(同步):文本序列标注

5、从RNN到LSTM

RNN的模型可以简化成如下图的形式：

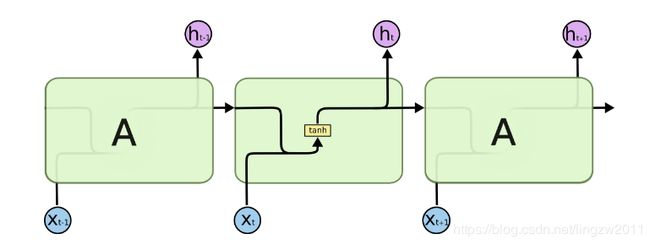
图中可以很清晰看出在隐藏状态h_t由x_t和h_t-1得到，得到h_t后一方面用于当前层的模型损失计算，另一方面用于计算下一层的h_t+1。

RNN算法处理时间序列的问题的效果很好, 但是仍然存在着一些问题, 其中较为严重的是容易出现梯度消失或者梯度爆炸的问题。

深度学习中，激活函数不断嵌套使得参数的梯度在后边越来越小或越来越大，当参数值在后边越来越小（梯度消失）或越来越大（梯度爆炸），RNN前边信息都很快被丢失，后面时间的节点对于前面时间的节点感知力下降，也就是忘事儿。

由于RNN梯度消失或者梯度爆炸的问题，就出现了一系列的改进的算法，最常见的是LSTM（Long Short Term Memory），结构如下：

6、LSTM模型结构剖析

LSTM结构图中可以看出，在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h_t，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为C_t。如下图所示：

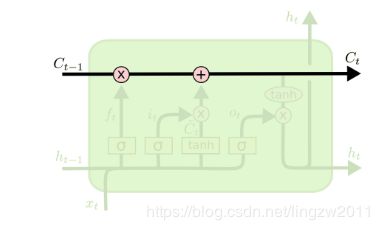
除了细胞状态，LSTM图中还有了很多奇怪的结构，这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。

6.1 遗忘门

遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：

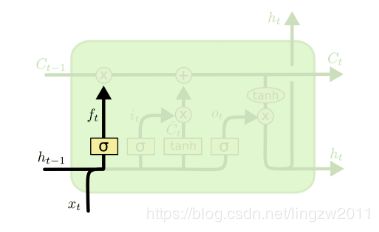
图中输入的有上一序列的隐藏状态h_t−1和本序列数据x_t，通过激活函数σ(sigmoid)，得到遗忘门的输出f_t；由于sigmoid函数的输出f_t在[0,1]之间，因此这里的输出代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为：

f_t = σ(W_fh_t−1 + U_fx_t + b_f)

其中W_f、U_f、b_f为线性关系的系数和偏倚。

6.2 输入门

输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：

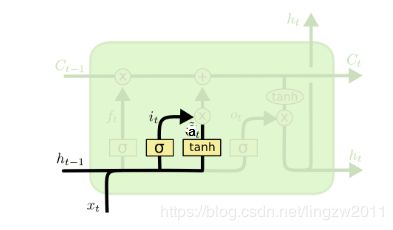
从图中可以看到输入门由两部分组成，第一部分使用了 σ(sigmoid) 激活函数，输出为_t；第二部分使用了tanh激活函数，输出为a_t，两者的结果后面会相乘再去更新细胞状态。用数学表达式即为：

i_t = σ(W_ih_t−1 + U_ix_t + b_i)

a_t = tanh(W_ah_t−1 + U_ax_t + b_a)

其中W_i、U_i、b_i、W_a、U_a、b_a为线性关系的系数和偏倚。

6.3 细胞状态

前面的遗忘门和输入门的结果都会作用于细胞状态C_t；如下图所示：

细胞状态C_t由两部分组成，第一部分是C_t−1和遗忘门输出f_t的乘积，第二部分是输入门的i_t和a_t的乘积，用数学表达式即为：

C_t = C_t−1⊙f_t + i_t⊙a_t

其中⊙为哈达马积。

6.4 输出门

从图中可以看出，隐藏状态h_t的更新由两部分组成，第一部分是o_t, 它由上一序列的隐藏状态h_t−1和本序列数据x_t，以及激活函数σ(sigmoid) 得到，第二部分由隐藏状态C_t和tanh激活函数组成, 用数学表达式即：

o_t = σ(W_oh_t−1 + U_ox_t+b_o)

h_t = o_t⊙tanh(C_t)

其中W_o、U_o、b_o为线性关系的系数和偏倚。

7、LSTM前向传播算法

LSTM模型结构有两个隐藏状态h_t、C_t，模型参数几乎是RNN的4倍，因为现在多了W_f、U_f、b_f、W_a、U_a、b_a、W_i、U_i、b_i、W_o、U_o、b_o这些参数。

前向传播过程在每个序列索引位置的过程为：

1. 更新遗忘门输出：
   f_t = σ(W_fh_t−1 + U_fx_t + b_f)
2. 更新输入门两部分输出：
   i_t = σ(W_ih_t−1 + U_ix_t + b_i)
   a_t = tanh(W_ah_t−1 + U_ax_t+b_a)
3. 更新细胞状态：
   C_t = C_t−1⊙f_t + i_t⊙a_t
4. 更新输出门输出：
   o_t = σ(W_oh_t−1 + U_ox_t + b_o)
   h_t = o_t⊙tanh(C_t)
5. 更新当前序列索引预测输出：
   y_t = σ(Vh_t + c)

8、MNIST图片识别实验

8.1 函数

1) BasicLSTMCell()函数

tf.contrib.rnn.BasicLSTMCell
(
num_units,
forget_bias=1.0,
input_size=None,
state_is_tuple=True,
activation=tanh,
reuse=None
)

num_units: 并不是指有多少个相互独立的LSTM，而是指LSTM单元内部的三个门的参数，相当于前馈神经网络，num_units就是这个层的隐藏神经元个数，所有时序是共享的。
forget_bias: 遗忘的偏置是0-1的数，1全记得，0全忘记
input_size: 该参数已被弃用
state_is_tuple: 默认设为True，返回 (c_state , m_state)的二元组，建议设为True。
activation: 状态之间转移的激活函数
reuse: Python布尔值, 描述是否重用现有作用域中的变量。

2) dynamic_rnn()函数

tf.nn.dynamic_rnn
(cell,
inputs,
sequence_length=None,
initial_state=None,
dtype=None,
parallel_iterations=None,
swap_memory=False,
time_major=False,
scope=None)

cell：用于神经网络的RNN神经元，如BasicRNNCell、BasicLSTMCell
inputs： 如果time_major的值为False，inputs的形状必须为[batch_size,max_time,depth]；如果time_major的值为True，inputs的形状必须为[max_time,batch_size,depth]，其中batch_size表示批大小，max_time是时间序列大小，depth表示单个时刻的序列向量的大小。
sequence_length：一个int32 / int64向量，大小为batch_size，如果指定了这个参数，那么tf会对长度不够的输入在尾部填0。
initial_state：初始化状态 (可选)， 需要是一个[batch_size, cell.state_size]形状的tensor.一般初始化为0。
dtype：可选）初始状态和预期输出的数据类型。 如果未提供initial_state或RNN状态具有异构dtype，则为必需。
parallel_iterations：（默认：32）。 并行运行的迭代次数。 那些没有任何时间依赖性并且可以并行运行的操作将会是。 此参数为空间换取时间。 值>> 1使用更多的内存，但花费的时间更少，而更小的值使用更少的内存，但计算需要更长的时间。
swap_memory：透明地交换前向推理中产生的张量，但是需要GPU支持back prop。 这允许对通常不适合单个GPU的RNN进行训练，并且性能损失非常小（或没有）。
time_major：默认值为False。
scope：用于创建子图的VariableScope; 默认为“rnn”。
返回值：outputs表示所有时刻的输出。如果time_major=false，其shape=(batch_size,max_time,cell.output_size)，如果time_major=true，其shape=(max_time,batch_size,cell.output_size)；state表示最后的状态，如果cell.state_size是一个int，这将被shaped [batch_size，cell.state_size]。 如果它是一个TensorShape，这将形成[batch_size] + cell.state_size。 如果它是一个（可能是嵌套的）int或TensorShape的元组，它将是一个具有相应形状的元组。

8.2 代码

1) 架构图

MNIST数据集中，图像的像素是28*28，每一张都可以看成拥有28行28个像素的图像，对图片进行序列化，将网络按28个时间步展开，以使在每一个时间步中，可以输入一行28个像素，从而经过28个时间步输入整张图像，架构图如下：

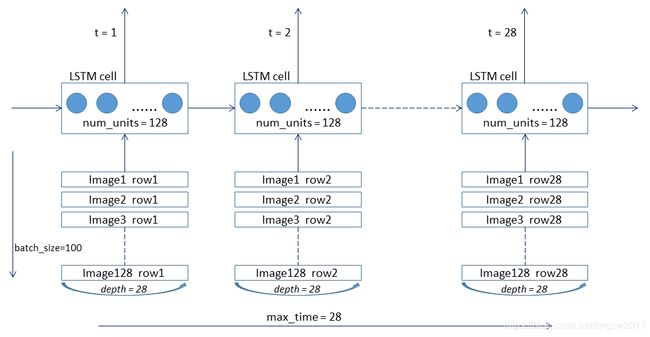
2) 详细代码

# -*- coding: utf-8 -*-
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# 参数设置
BATCH_SIZE = 100        # 图片批次大小
MAX_TIME = 28           # 时间序列大小
DEPTH = 28              # 每时刻序列长度
NUM_UNITS = 128         # LSTM 单元格中的单元数
N_CLASSES = 10          # 输出大小，0-9十个数字的概率

# 定义输入、输出占位符，输入把每个图像都组成28*28的向量，输出是一个长度为10的向量
x = tf.placeholder(tf.float32, [None, MAX_TIME * DEPTH])
y_ = tf.placeholder(tf.float32, [None, N_CLASSES])

# 定义LSTM cell
lstm_cell = tf.contrib.rnn.BasicLSTMCell(num_units=NUM_UNITS)
# 重建RNN的输入维度
inputs = tf.reshape(x, [-1, MAX_TIME, DEPTH])
# 定义RNN网络
outputs,state = tf.nn.dynamic_rnn(
    cell=lstm_cell,
    inputs=inputs,
    dtype=tf.float32
)
# 如果time_major=false，其shape=(batch_size,max_time,cell.output_size)，取中间维度 outputs[:, -1, :]
# state=[batch_size，cell.state_size],取最后的状态，state[1] = outputs[:, -1, :]
# 添加全连接层，inputs：输入该网络层的数据 units：输出的维度大小
output = tf.layers.dense(inputs=outputs[:, -1, :], units=N_CLASSES)

# **********************交叉熵函数**********************
# tf.nn.softmax_cross_entropy_with_logits
# tf.nn.sparse_softmax_cross_entropy_with_logits
# tf.losses.softmax_cross_entropy
# tf.losses.sparse_softmax_cross_entropy
# **********************交叉熵函数**********************

# onehot_labels：[batch_size, num_classes]目标是一个hot-encoded标签。 logits：[batch_size, num_classes]logits网络的输出。
cross_entropy = tf.losses.softmax_cross_entropy(onehot_labels=y_, logits=output)
# 梯度下降
train_step = tf.train.AdamOptimizer(0.001).minimize(cross_entropy)
# 定义分类的准确率
correct_prediction = tf.equal(tf.argmax(y_, axis=1), tf.argmax(output, axis=1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# session初始化并调用
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())

# 迭代优化模型 迭代20000次
for i in range(20000):
    batch_xs, batch_ys = mnist.train.next_batch(BATCH_SIZE)
    train_step.run(feed_dict={x: batch_xs, y_: batch_ys})
    if i % 100 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels})
        print("第{0}次训练，准确率：{1}".format(i+100, train_accuracy))

训练结果如下：
Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
第100次训练，准确率：0.10169999301433563
第200次训练，准确率：0.7672999501228333
第300次训练，准确率：0.8756000399589539
第400次训练，准确率：0.9099001884460449
第500次训练，准确率：0.9263001084327698
第600次训练，准确率：0.9450001120567322
第700次训练，准确率：0.9473000764846802
第800次训练，准确率：0.9571002125740051
第900次训练，准确率：0.9537001252174377
第1000次训练，准确率：0.9572000503540039
…
…
…
第19000次训练，准确率：0.989000141620636
第19100次训练，准确率：0.9894001483917236
第19200次训练，准确率：0.9882001280784607
第19300次训练，准确率：0.9882001876831055
第19400次训练，准确率：0.9861000776290894
第19500次训练，准确率：0.9877001047134399
第19600次训练，准确率：0.9868001341819763
第19700次训练，准确率：0.9879001379013062
第19800次训练，准确率：0.9889001846313477
第19900次训练，准确率：0.9897000789642334
第20000次训练，准确率：0.9879001379013062

训练的准确率在98%~99%之间，还行！

菜鸟一枚，发表博客的主要目的是为了记录tensorflow机器学习中的点滴，方便自己以后查阅，如果有错误的地方，还请大家多提宝贵意见。