高斯混合聚类

一、问题引入
我们已经使用过k-means算法解决聚类问题。这个算法的突出优点是简单易用，计算量也不多。然而，往往过于简单也是一个缺点。假设聚类可以表示为单个点往往会过于粗糙。举一个例子，如下图所示：

这个例子中数据位于同心圆。在这种情况下，标准的K均值由于两个圆的均值位置相同，无法把数据划分成簇（所以上面有一个绿点不知道该往哪跑，因为它没有簇）。因此，以距离模型为聚类标准的方法不一定都能成功适用。为了解决这些缺点，我们介绍一种用统计混合模型进行聚类的方法——高斯混合模型（Gaussian Mixture Model, GMM）。这种聚类方法得到的是每个样本点属于各个类的概率，而不是判定它完全属于一个类，所以有时也会被称为软聚类。

二、问题分析
1.我们使用EM算法来求解高斯混合模型的相关参数。算法流程如下：
Repeat until convergence {
E-step: For each i, j, set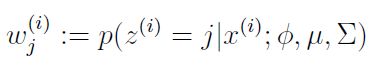

M-step: Update parameters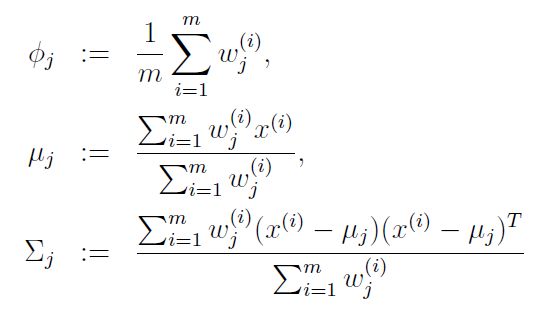

}
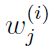其中是隐含变量z服从的先验分布，其余两个参数是混合高斯分布的均值(μ)和协方差(Σ)。是隐含变量z属于类别j的后验概率，其可以根据贝叶斯公式计算得到：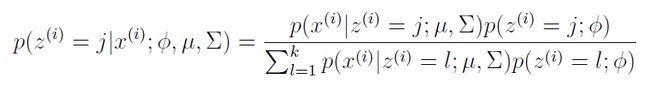

2.EM算法求解GMM的简单推导
下面我们只对M-step作简单推导。在M-step中，我们需要最大化一个关于参数Φ,μ,Σ的式子：

很自然地会想到对逐个参数求偏导数。先对μ求偏导数，得：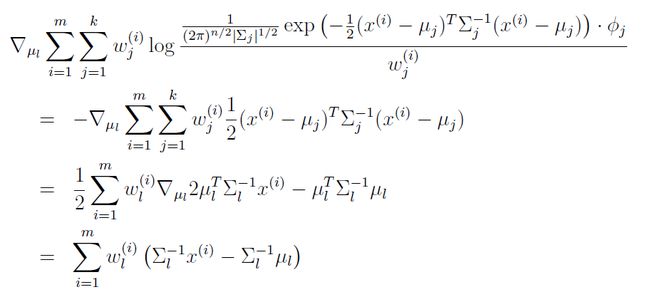

令其等于0，得到：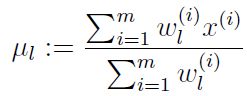

其次，对Φ求偏导数，可以先把和Φ无关的项去掉，简化求导计算：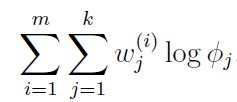

因为是先验分布，因此它有一个约束条件，就是。这时需要引入朗格朗日乘子，设拉格朗日函数如下：

对拉格朗日函数求偏导数，得：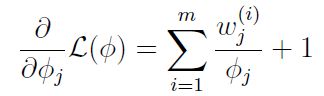

令偏导数等于0，得：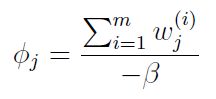

事实上，我们有：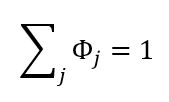

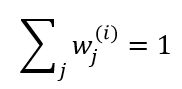
因为它们都是概率分布。对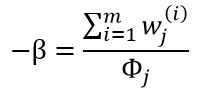的分子分母同时求和，得：

最后的迭代式为：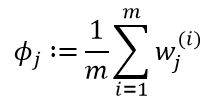

求解Σ的迭代式也是通过求解拉格朗日函数对Σ的偏导数并令其等于0求得，在此不再赘述。

三、代码实现（Matlab）

%% 导入数据
load('kmeansdata')

%% 初始化混合模型参数
K = 3; 
% 随机初始化均值和协方差
means = randn(K,2);
for k = 1:K
    covs(:,:,k) = rand*eye(2);
end
priors = repmat(1/K,1,K);   % 初始化，假设隐含变量服从先验均匀分布

%% 主算法
MaxIts = 100;   % 最大迭代次数
N = size(X,1);  % 样本数
q = zeros(N,K); % 后验概率
D = size(X,2);  % 维数
cols = {'r','g','b'};
plotpoints = [1:1:10,12:2:30 40 50];
B(1) = -inf;
converged = 0;
it = 0;
tol = 1e-2;
while 1
    it = it + 1;
    % 把乘除化为对数加减运算，防止乘积结果过于接近于0
    for k = 1:K
        const = -(D/2)*log(2*pi) - 0.5*log(det(covs(:,:,k)));
        Xm = X - repmat(means(k,:),N,1);
        temp(:,k) = const - 0.5 * diag(Xm*inv(covs(:,:,k))*Xm');
    end

    % 计算似然下界
    if it > 1
        B(it) = sum(sum(q.*log(repmat(priors,N,1)))) + sum(sum(q.*temp)) - sum(sum(q.*log(q)));
        if abs(B(it)-B(it-1))1;

        end
    end  
    if converged == 1 || it > MaxIts
        break
    end
    % 计算每个样本属于第k类的后验概率
    temp = temp + repmat(priors,N,1);
    q = exp(temp - repmat(max(temp,[],2),1,K));

    q(q < 1e-60) = 1e-60;
    q(q > (1-(1e-60))) = 1-(1e-60);
    q = q./repmat(sum(q,2),1,K);
    % 更新先验分布
    priors = mean(q,1);
    % 更新均值
    for k = 1:K
        means(k,:) = sum(X.*repmat(q(:,k),1,D),1)./sum(q(:,k));
    end
    % 更新方差
    for k = 1:K
        Xm = X - repmat(means(k,:),N,1);
        covs(:,:,k) = (Xm.*repmat(q(:,k),1,D))'*Xm;
        covs(:,:,k) = covs(:,:,k)./sum(q(:,k));
    end 
end

%% plot the data
figure(1);hold on;

plot(X(:,1),X(:,2),'ko');

for k = 1:K
    plot_2D_gauss(means(k,:), covs(:,:,k), -2:0.1:5,-6:0.1:6);
end
ti = sprintf('After %g iterations',it);
title(ti)
%% 绘制似然下界迭代过程图
figure(2);hold off
plot(2:length(B),B(2:end),'k');
xlabel('Iterations');
ylabel('Bound');

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79

这里我们随机选择3个组分的均值和协方差来进行初始化，并且假设一个均匀的先验分布。然后算法中依次对均值、协方差、后验概率、先验分布进行迭代更新。以最大化似然下界的两次迭代之差小于一个很小的常数作为迭代的停止条件。选择K=3，绘图效果如下：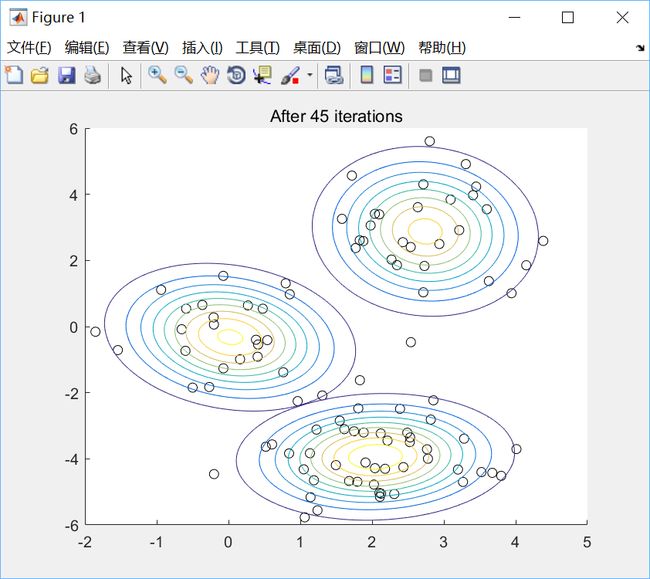

这里我们不显式地把所有样本点划归某一个类，只是给出它们分别属于每一个类的概率分布。我们还可以看到似然下界的收敛情况：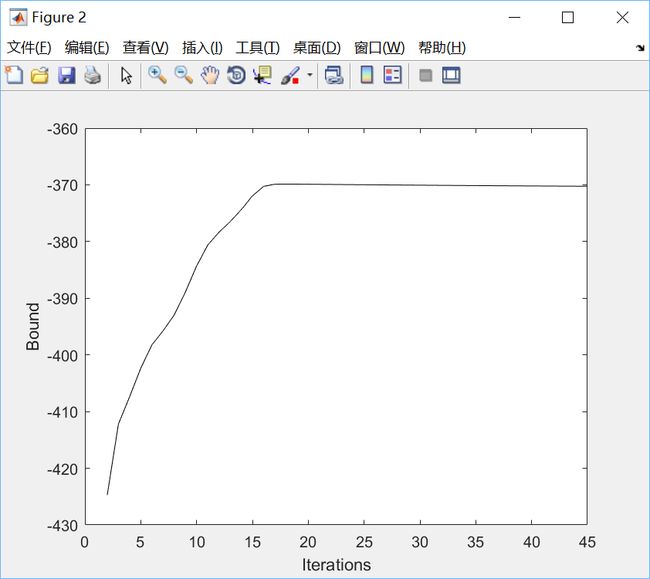

四、总结
关于聚类问题我们分析至此。然而这些东西只是聚类问题中的冰山一角，还有层级聚类、谱聚类和功能聚类等。作为学习的过程，了解两三个典型的案例已经足够可以让我们对聚类问题有一个基本的理解。一路坚持下来，真心不易。阅读全英文的讲义，推导枯燥的公式，有时公式不记得了还要到处翻书，还有冗长复杂的编程……虽然付出了相当多的时间和精力，但收获也是巨大的！