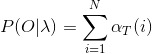liuy9803

机器学习之HMM

机器学习最重要的任务，是根据已观测到的数据（如训练样本）对感兴趣的未知变量（如类别标记）进行推断（inference）。概率图模型是用图表达变量相关关系的概率模型，分为“有向无环图模型/贝叶斯网”和“无向图模型/马尔可夫网”两类。

一、马尔可夫性质

马尔可夫性质（Markov property）是概率论中的一个概念，当一个随机过程在给定现在状态以及所有过去状态的情况下，其未来状态的条件概率分布仅依赖于当前状态（即在给定当前状态后，过去与未来状态是条件独立的），那么这个随机过程就具有马尔可夫性质，具有马尔可夫性质的过程称为马尔可夫过程。

应用有马尔可夫链、布朗运动等。

二、马尔可夫链

马尔可夫链（Markov Chain）是指具有马尔可夫性质的离散事件随机过程，在给定当前状态的情况下，该过程中过去的状态对于预测未来的状态是无关的。

在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态不变。状态的改变叫做转移，状态改变的相关概率叫做转移概率。

应用有随机漫步、排队理论建模、马尔可夫链蒙特卡洛方法MCMC、统计学建模、作为信号模型用于熵编码、人口过程、基因预测、谱曲等。

三、隐马尔可夫模型

HMM（Hidden Markov Model）是关于时序的概率模型，属于生成式模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列（state sequence），再由各个状态生成一个观测而产生的观测随机序列（observation sequence）的过程（双重随机过程）。

应用有语音/行为/模式识别、自然语言处理、生物信息DNA分析、故障诊断等。

1、HMM的形式定义

HMM涉及到的参数有：（隐含）状态序列I、观测序列O、初始（隐含）状态概率向量π、（隐含）状态转移概率矩阵A、观测概率矩阵B。

（1）设 $Q=\left \{ q_{1},q_{2},...,q_{N} \right \}$ 是所有可能的状态集合， $V=\left \{ v_{1},v_{2},...,v_{M} \right \}$ 是所有可能的观测集合，N是可能的状态总数，M是可能的观测总数；

（2） $I=\left \{ i_{1},i_{2},...,i_{T} \right \}$ 是长度为T的状态序列， $O=\left \{ o_{1},o_{2},...,o_{T} \right \}$ 是对应的观测序列；

（3） $A=[a_{ij}]_{N*N}$ 是状态转移概率矩阵，其中 $a_{ij}=P(i_{t+1}=q_{j}|i_{t}=q_{i})$ ，是在时刻t处于状态 $q_{i}$ 的条件下，在时刻t+1转移到状态 $q_{j}$ 的概率。

（4） $B=[b_{i}(k)]_{N*M}$ 是观测概率矩阵，其中 $b_{i}(k)=P(o_{t}=v_{k}|i_{t}=q_{i})$ ，，是在时刻t处于状态 $q_{i}$ 的条件下生成观测 $v_{k}$ 的概率。

（5） $\pi =[\pi _{i}]_{1*N}$ 是初始状态概率向量，其中 $\pi _{i}=P(i_{1}=q_{i})$ ，i=1,2,...,N 是在时刻t=1处于状态 $q_{i}$ 的概率。

π和A决定了状态序列、B决定观测序列，因此HMM可以使用三要素表示：λ=(A,B,π)。

2、HMM的观测序列生成过程

已知HMM模型λ，观测序列长度为T，则观测序列O的生成过程：

（1）由初始状态分布π产生状态 $i_{1}$

（2）令t=1

（3）按照状态it的观测概率分布 $b_{i_{t}}(k)$ 生成 $o_{t}$

（4）按照状态的状态转移概率分布 $a_{i_{t}i_{t+1}}$ 产生状态 $i_{t+1}$

（5）令t=t+1，如果t

3、HMM的两个基本假设：

（1）齐次马尔可夫性假设

假设隐藏的马尔可夫链在任意t时刻的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻t无关：

$P(i_{t}|i_{t-1},o_{t-1},i_{t-2},o_{t-2},...,i_{1},o_{1})=P(i_{t}|i_{t-1})$

（2）观测独立性假设

假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他的状态及观测无关：

$P(o_{t}|i_{T},o_{T},i_{T-1},o_{T-1},...,i_{t+1},o_{t+1},i_{t},i_{t-1},o_{t-1},...,i_{1},o_{1})=P(o_{t}|i_{t})$

4、HMM的3个基本问题

（1）概率计算问题：求P(O|λ)

给定模型λ，计算其生成的观测序列O的概率P(O|λ)，即评估模型与观测序列之间的匹配程度。

（2）学习问题：求λ

给定观测序列O，调整模型λ的参数（MLE），使得在该模型下观测序列出现的概率P(O|λ)最大；

即训练模型使其能够更好地描述观测数据。

（3）预测问题（decoding）：求I

给定模型λ和观测序列O，求使观测序列条件概率P(I|O)最大的状态序列I，即根据观测序列推断最匹配的状态序列。

四、概率计算问题

1、直接计算法（brute）

给定模型λ，计算其生成的观测序列O的概率P(O|λ)。最直接的方式是按照概率公式，列举所有可能的长度为T的状态序列 $I=\left \{ i_{1},i_{2},...,i_{T} \right \}$ ，求状态序列I与观测序列 $O=\left \{ o_{1},o_{2},...,o_{T} \right \}$ 的联合概率P(I,O|λ)，然后对所有可能的状态序列求和（边际化marginalization），从而得到最终的概率P(O|λ)。

$P(I|\lambda)=\pi _{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}}...a_{i_{T-1}i_{T}}$

$P(O|I,\lambda)=b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})...b_{i_{T}}(o_{T})$

$P(O,I|\lambda)=P(O|I,\lambda)P(I|\lambda)=\pi _{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}}...a_{i_{T-1}i_{T}}b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})...b_{i_{T}}(o_{T})$

$P(O|\lambda)=\sum _{I}P(O|I,\lambda)P(I|\lambda)=\sum _{i_{1},i_{2},...,i_{T}}\pi _{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}}...a_{i_{T-1}i_{T}}b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})...b_{i_{T}}(o_{T})$

这种算法的计算量很大 $O(TN^{T})$ ，概念上可解但实际应用中不可行。

2、前向算法

前向概率指的是给定模型λ，定义到时刻t部分的观测序列为 $o_{1},o_{2},...,o_{t}$ ，且状态为 $q_{i}$ 的概率为前向概率，记作：

前向算法

（1）初始化前向概率，是初始时刻的状态 $i_{1}$ 和观测 $o_{1}$ 的联合概率。对状态所有的取值总数有：

$\alpha _{1}(i)=P(o_{1},i_{1}=q_{i}|\lambda)=\pi_{i}b_{i}(o_{1})$

（2）前向递推，设 $\alpha _{t}(i)$ 是时刻t观测到 $o_{1},o_{2},...,o_{t}$ 且此时处于 $q_{i}$ 状态的前向概率；计算 $a_{ij}\alpha _{t}(i)$ 就是时刻t观测到o1,o2,...,ot且此时处于 $q_{i}$ 状态而在时刻t+1转移到状态 $q_{j}$ 的联合概率，对其在时刻t所有可能的N个状态求和再乘以观测概率：

$\alpha _{t+1}(j)=b_{j}(o_{t+1})\sum_{i=1}^{N}\alpha _{t}(i)a_{ij}$

（3）将状态对应的概率求和消去，即可得到O的边缘概率：

$\alpha _{T}(i)=P(o_{1},o_{2},...,o_{T},i_{T}=q_{i}|\lambda)$

$P(O|\lambda)=\sum_{i=1}^{N}\alpha _{T}(i)$

前向概率的计算量为 $O(N^{2}T)$ ，减少计算量的原因在于每一次计算直接引用前一个时刻的计算结果，避免了重复计算。

3、后向算法

后向概率指的是给定模型λ，定义在时刻t状态为 $q_{i}$ 的条件下，从t+1到T的部分观测序列为 $o_{t+1},o_{t+2},...,o_{T}$ 的概率为后向概率，记作：

后向算法

（1）初始化后向概率，对最终时刻T的所有状态，i=1,2,...,N有：

$\beta _{T}(i)=1$

（2）后向递推，在时刻t+1所有可能的N个状态 $q_{j}$ 的转移概率 $a_{ij}$ ，乘以此状态下的观测概率 $b_{j}(o_{t+1})$ ，再乘以状态 $q_{j}$ 之后的后向概率 $\beta _{t+1}(j)$ 即可得到t时刻t状态为 $q_{i}$ 的后向概率。对，，有：

$\beta _{t}(i)=\sum _{j=1}^{N}a_{ij}b_{j}(o_{t+1})\beta _{t+1}(j)$

（3）将状态对应的概率求和消去，即可得到O的边缘概率：

$P(O|\lambda )=\sum_{i=1}^{N}\pi_{i}b_{i}(o_{1})\beta_{1}(i)$

利用前向概率和后向概率的定义可以将观测序列P(O|λ)统一写成：

$P(O|\lambda )=\sum_{i=1}^{N} \sum_{j=1}^{N}\alpha _{t}(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)$

4、单个状态的概率

给定模型λ和观测序列O，在时刻t处于状态 $q_{i}$ 的概率记为 $\gamma _{t}(i)$ ：

$\gamma _{t}(i)=P(i_{t}=q_{i}|O,\lambda )=\frac{P(i_{t}=q_{i},O|\lambda)}{P(O|\lambda)}$

由前向、后向概率的定义可知：

$P(i_{t}=q_{i},O|\lambda)=\alpha _{t}(i)\beta _{t}(i)$

于是得到：

$\gamma _{t}(i)=\frac{\alpha _{t}(i)\beta _{t}(i)}{\sum_{j=1}^{N}\alpha _{t}(j)\beta _{t}(j)}$

单个状态概率的意义在于判断每个时刻最可能存在的状态，从而可以得到一个状态序列作为最终的预测结果。

5、两个状态的联合概率

给定模型λ和观测序列O，在时刻t处于状态 $q_{i}$ 且在时刻t+1处于状态 $q_{j}$ 的概率记为 $\xi _{t}(i,j)$ ：

$\xi _{t}(i,j)=P(i_{t}=q_{i},i_{t+1}=q_{j}|O,\lambda)\\\\=\frac{P(i_{t}=q_{i},i_{t+1}=q_{j},O|\lambda)}{P(O|\lambda)}\\\\\\=\frac{P(i_{t}=q_{i},i_{t+1}=q_{j},O|\lambda)}{\sum_{i,j=1}^{N}P(i_{t}=q_{i},i_{t+1}=q_{j},O|\lambda)}\\\\\\=\frac{\alpha _{t}(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)}{\sum_{i,j=1}^{N}\alpha _{t}(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)}$

6、将 $\gamma _{t}(i)$ 和 $\xi _{t}(i,j)$ 对各个时刻t求和，可以得到一些有用的期望值

（1）在观测O下状态i出现的期望值： $\sum_{t=1}^{T}\gamma _{t}(i)$

（2）在观测O下由状态i转移的期望值： $\sum_{t=1}^{T-1}\gamma _{t}(i)$

（3）在观测O下由状态i转移到状态j的期望值： $\sum_{t=1}^{T-1}\xi _{t}(i,j)$

五、学习问题

HMM的学习问题，根据训练数据是否包含状态序列分两类：若包含O和I，则可用监督学习算法实现；若只包含O，则需要用非监督学习算法Baum-Welch（EM）算法求解。

1、监督学习方法

由大数定理结论‘频率的极限是概率’直接得出HMM的参数估计。

（1）设时刻t处于状态i、时刻t+1转移到状态j的频数为 $A_{ij}$ ，则状态转移概率 $a_{ij}$ 的估计为：

$\hat{a}_{ij}=\frac{A_{ij}}{\sum_{j=1}^{N}A_{ij}}\; \; \; \; i=1,2,...,N;\; j=1,2,...,N$

（2）设样本中状态为j且观测为k的频数是 $B_{jk}$ ，则观测概率 $b_{j}(k)$ 的估计为：

$\hat{b}_{j}(k)=\frac{B_{jk}}{\sum_{k=1}^{M}B_{jk}}\; \; \; \; j=1,2,...,N;\; k=1,2,...,M$

（3）初始状态概率 $\pi _{i}$ 的估计为样本总数中初始状态为 $q_{i}$ 的频率。

2、非监督学习方法（Baum-Welch算法）

给定观测数据O，状态序列I未知，则HMM为含有隐变量的概率模型 $P(O|\lambda )=\sum_{I}P(O|I,\lambda)P(I|\lambda)$ ，然后用EM算法进行参数估计。步骤如下：

（1）确定完全数据(O,I)的对数似然函数

$(O,I)=(o_{1},o_{2},...,o_{T},i_{1},i_{2},...,i_{T})$ ，它的对数似然函数是lnP(O,I|λ)

（2）E步求Q函数

$Q(\lambda ,\bar{\lambda} )=\sum _{I}P(I|O,\lambda )logP(O,I|\lambda )\\\\=\sum _{I}\frac{P(O,I|\bar{\lambda} )}{P(O|\bar{\lambda} )}logP(O,I|\lambda)\\\\\propto \sum _{I}P(O,I|\bar{\lambda} )logP(O,I|\lambda)$

其中， $\bar{\lambda }$ 是HMM参数的当前估计值，需要将其极大化。

$\because P(O,I|\lambda)=\pi _{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}}...a_{i_{T-1}i_{T}}b_{i_{1}}(o_{1})b_{i_{2}}(o_{2})...b_{i_{T}}(o_{T})$

$\therefore Q(\lambda |\bar{\lambda} )=\sum _{I}P(O,I|\bar{\lambda})\ln\pi_{i_{1}}+\sum _{I}P(O,I|\bar{\lambda})\sum_{t=1}^{T-1}\ln a_{i_{t}i_{t+1}}+\sum _{I}P(O,I|\bar{\lambda})\sum _{t=1}^{T}\ln b_{i_{t}}(o_{t})$

（3）M步极大化Q函数，使用Lagrange乘子法分别求π、A、B的值：

$\sum _{I}P(O,I|\bar{\lambda})\ln\pi_{I}=\sum_{i=1}^{N}P(O,i_{1}=i|\bar{\lambda })\ln\pi_{i}$

$l(\pi_{i})=\sum_{i=1}^{N}P(O,i_{1}=i|\bar{\lambda })\ln \pi_{i}+\varphi \left ( \sum_{i=1}^{N}\ln \pi_{i}-1 \right )$

$\frac{\partial l(\pi_{i})}{\partial \pi_{i}}=0\Rightarrow P(O,i_{1}=i|\bar{\lambda })+\varphi \pi_{i}=0$

对i求和消去i，可得： $\varphi =-P(O|\bar{\lambda })$

$\therefore \pi _{i}=\frac{P(O,i_{1}=i|\bar{\lambda })}{P(O|\bar{\lambda })}=\gamma _{1}(i)$

$\sum _{I}P(O,I|\bar{\lambda})\sum_{t=1}^{T-1}\ln a_{i_{t}i_{t+1}}=\sum _{i=1}^{N}\sum_{j=1}^{N}\sum_{t=1}^{T-1}P(O,i_{t}=i,i_{t+1}=j|\bar{\lambda })\ln a_{ij}$

$l(a_{ij})=\sum _{i=1}^{N}\sum_{j=1}^{N}\sum_{t=1}^{T-1}P(O,i_{t}=i,i_{t+1}=j|\bar{\lambda })\ln a_{ij}+\tau \left ( \sum _{i=1}^{N}\sum_{j=1}^{N}a_{ij}-N \right )$

$\frac{\partial l(a_{ij})}{\partial a_{ij}}=0\Rightarrow \sum_{t=1}^{T-1}P(O,i_{t}=i,i_{t+1}=j|\bar{\lambda })+\tau a_{ij}=0$

对i、j求和消去i、j，可得： $\tau =\sum_{t=1}^{T-1}P(O,i_{t}=i,|\bar{\lambda })$

$\therefore a_{ij}=\frac{\sum_{t=1}^{T-1}P(O,i_{t}=i,i_{t+1}=j|\bar{\lambda })}{\sum_{t=1}^{T-1}P(O,i_{t}=i|\bar{\lambda })}= \frac{\sum_{t-1}^{T}\xi _{t}(i,j)}{\sum_{t-1}^{T}\gamma _{t}(i)}$

$\sum _{I}P(O,I|\bar{\lambda})\sum _{t=1}^{T}\ln b_{i_{t}}(o_{t})=\sum_{j=1}^{N}\sum_{t=1}^{T}P(O,i_{t}=j|\bar{\lambda})\ln b_{j}(o_{t})$

$l(b_{j}(o_{t}))=\sum_{j=1}^{N}\sum_{t=1}^{T}P(O,i_{t}=j|\bar{\lambda})\ln b_{j}(o_{t})+\eta \left ( \sum_{j=1}^{N}\sum_{k=1}^{M}b_{j}(o_{t}=v_{k})-M \right )$

$\frac{\partial l(b_{j}(o_{t}))}{\partial b_{j}(o_{t})}=0\Rightarrow \sum_{j=1}^{N}\sum_{t=1}^{T}P(O,i_{t}=j|\bar{\lambda})+\eta b_{j}(o_{t})=0$

对j、k求和消去j、k，可得： $\eta =\sum_{t=1}^{T-1}P(O,i_{t}=j,|\bar{\lambda })$

$\therefore b_{j}(k)=\frac{\sum_{t=1}^{T}P(O,i_{t}=j|\bar{\lambda})I(o_{t}=v_{k})}{\sum_{t=1}^{T}P(O,i_{t}=j|\bar{\lambda})}=\frac{\sum_{t=1,o_{t}=v_{k}}^{T}\gamma _{t}(j)}{\sum_{t=1}^{T}\gamma _{t}(j)}$

Baum-Welch算法流程：

给定观测序列 $O=\left \{ o_{1},o_{2},...,o_{T} \right \}$

随机初始化 $a_{ij}^{(0)}$ ， $b_{j}(k)^{(0)}$ ， $\pi_{i}^{(0)}$ ，得到模型 $\lambda ^{(0)}=(\pi ^{(0)},A^{(0)},B^{(0)})$ ；

对每个样本使用前向后向算法求出 $\gamma _{t}(i)$ ， $\xi _{t}(i,j)$ ；

更新模型参数 $a_{ij}^{(n)}$ ， $b_{j}(k)^{(n)}$ ， $\pi_{i}^{(n)}$ ；

如果参数收敛则停止，否则继续迭代。

六、预测问题

HMM的预测问题是给定模型λ和观测序列O，求最可能的状态序列，主要包含近似算法和Viterbi算法两种。

1、近似算法

将每个时刻t最有可能出现的状态 $i_{t}^{*}$ 合并成为最终要预测的状态序列 $I^{*}=\left \{ i_{1}^{*},i_{2}^{*},...,i_{T}^{*} \right \}$ 。在时刻t处于状态 $q_{i}$ 的最大概率为：

$\gamma _{t}(i)=\frac{\alpha _{t}(i)\beta _{t}(i)}{P(O|\lambda)}=\frac{\alpha _{t}(i)\beta _{t}(i)}{\sum_{j=1}^{N}\alpha _{t}(j)\beta _{t}(j)}$

$i_{t}^{*}=\arg \max _{1\leqslant i\leqslant N}[\gamma _{t}(i)]$

近似算法的优点是计算简单，缺点是不能保证预测的I*是最有可能的I，因为I*可能有实际不发生的部分。

2、Viterbi算法

使用动态规划（dynamic programming）的思路求出概率最大的路径（最优路径），一条路径对应一个状态序列。递推计算时刻状态为i的所有单个路径 $(i_{1},i_{2},...,i_{t})$ 中概率值最大的一个为 $\delta _{t}(i)$ ，对应的终结点为 $i_{T}^{*}$ 。从后向前逐步求得结点 $i_{T-1}^{*},...,i_{1}^{*}$ （ $\Psi _{t}(i)$ ），即可得到最优路径 $I^{*}=( i_{1}^{*},i_{2}^{*},...,i_{T}^{*})$ 。

$\delta _{t}(i)=\max_{i_{1},i_{2},...,i_{t-1}}P(i_{t}=i,i_{t-1},...,i_{1},o_{t},...,o_{1}|\lambda)$

$\Psi _{t}(i)=\arg\max_{1\leqslant j\leqslant N}[\delta _{t-1}(j)a_{ji}]$

Viterbi算法流程：

给定模型λ=(A,B,π)和观测序列 $O=\left \{ o_{1},o_{2},...,o_{T} \right \}$

（1）初始化，

$\delta _{1}(i)=\pi_{i}b_{i}(o_{1})$

$\Psi _{1}(i)=0$

（2）递推

$\delta _{t}(i)=\max_{i_{1},i_{2},...,i_{t-1}}P(i_{t}=i,i_{t-1},...,i_{1},o_{t},...,o_{1}|\lambda)=\max_{1\leqslant j\leqslant N}[\delta _{t-1}(j)a_{ji}]b_{i}(o_{t})$

$\Psi _{t}(i)=\arg\max_{1\leqslant j\leqslant N}[\delta _{t-1}(j)a_{ji}]$

（3）终止

$P^{*}=\max_{1\leqslant i\leqslant N}\delta _{T}(i)$

$i_{T}^{*}=\arg\max_{1\leqslant i\leqslant N}[\delta _{T}(i)]$

（4）回溯求得最优路径

$i_{t}^{*}=\Psi _{t+1}(i_{t+1}^{*})$

$I^{*}=( i_{1}^{*},i_{2}^{*},...,i_{T}^{*})$

参考资料：

《统计学习方法》、《机器学习——周志华》等

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
机器学习-聚类算法不良人龍木木机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
python中zeros用法_Python中的numpy.zeros()用法江平舟 python中zeros用法
numpy.zeros()函数是最重要的函数之一,广泛用于机器学习程序中。此函数用于生成包含零的数组。numpy.zeros()函数提供给定形状和类型的新数组,并用零填充。句法numpy.zeros(shape,dtype=float,order='C'参数形状：整数或整数元组此参数用于定义数组的尺寸。此参数用于我们要在其中创建数组的形状,例如(3,2)或2。dtype：数据类型(可选)此参数用于
【NumPy】深入解析numpy.zeros()函数二七830 numpy
欢迎莅临我的个人主页这里是我深耕Python编程、机器学习和自然语言处理（NLP）领域，并乐于分享知识与经验的小天地！博主简介：我是二七830，一名对技术充满热情的探索者。多年的Python编程和机器学习实践，使我深入理解了这些技术的核心原理，并能够在实际项目中灵活应用。尤其是在NLP领域，我积累了丰富的经验，能够处理各种复杂的自然语言任务。技术专长：我熟练掌握Python编程语言，并深入研究了机
【中国国际航空-注册_登录安全分析报告】风控牛验证码接口安全评测系列安全行为验证极验网易易盾智能手机
前言由于网站注册入口容易被黑客攻击，存在如下安全问题：1.暴力破解密码，造成用户信息泄露2.短信盗刷的安全问题，影响业务及导致用户投诉3.带来经济损失，尤其是后付费客户，风险巨大，造成亏损无底洞所以大部分网站及App都采取图形验证码或滑动验证码等交互解决方案，但在机器学习能力提高的当下，连百度这样的大厂都遭受攻击导致点名批评，图形验证及交互验证方式的安全性到底如何？请看具体分析一、中国国际航空PC
机器学习流形数据降维：UMAP 降维算法小嗷犬 Python 机器学习 #数据分析及可视化机器学习算法人工智能
✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。个人主页：小嗷犬的个人主页个人网站：小嗷犬的技术小站个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP（UniformManifoldApproximatio
七.正则化愿风去了
吴恩达机器学习之正则化（Regularization）http://www.cnblogs.com/jianxinzhou/p/4083921.html从数学公式上理解L1和L2https://blog.csdn.net/b876144622/article/details/81276818虽然在线性回归中加入基函数会使模型更加灵活，但是很容易引起数据的过拟合。例如将数据投影到30维的基函数上，模
机器学习-------数据标准化罔闻_spider 数据分析算法机器学习人工智能
什么是归一化，它与标准化的区别是什么？一作用在做训练时，需要先将特征值与标签标准化，可以防止梯度防炸和过拟合；将标签标准化后，网络预测出的数据是符合标准正态分布的—StandarScaler()，与真实值有很大差别。因为StandarScaler()对数据的处理是（真实值-平均值）/标准差。同时在做预测时需要将输出数据逆标准化提升模型精度：标准化/归一化使不同维度的特征在数值上更具比较性，提高分类
分享一个基于python的电子书数据采集与可视化分析 hadoop电子书数据分析与推荐系统 spark大数据毕设项目（源码、调试、LW、开题、PPT) 计算机源码社 Python项目大数据大数据 python hadoop 计算机毕业设计选题计算机毕业设计源码数据分析 spark毕设
作者：计算机源码社个人简介：本人八年开发经验，擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等，大家有这一块的问题可以一起交流！学习资料、程序开发、技术解答、文档报告如需要源码，可以扫取文章下方二维码联系咨询Java项目微信小程序项目Android项目Python项目PHP项目ASP.NET项目Node.js项目选题推荐项目实战|p
两种方法判断Python的位数是32位还是64位 sanqima Python编程电脑 python 开发语言
Python从1991年发布以来，凭借其简洁、清晰、易读的语法、丰富的标准库和第三方工具，在Web开发、自动化测试、人工智能、图形识别、机器学习等领域发展迅猛。 Python是一种胶水语言，通过Cython库与C/C++语言进行链接，通过Jython库与Java语言进行链接。 Python是跨平台的，可运行在多种操作系统上，包括但不限于Windows、Linux和macOS。这意味着用Py
使用最大边际相关性(MMR)选择示例：提高AI模型的多样性和相关性 aehrutktrjk 人工智能 easyui 前端 python
使用最大边际相关性(MMR)选择示例：提高AI模型的多样性和相关性引言在机器学习和自然语言处理领域，选择合适的训练示例对模型性能至关重要。最大边际相关性(MaximalMarginalRelevance,MMR)是一种优秀的示例选择方法，它不仅考虑了示例与输入的相关性，还注重保持所选示例之间的多样性。本文将深入探讨如何使用MMR来选择示例，以提高AI模型的性能和泛化能力。什么是最大边际相关性(MM
LangChain集成指南:如何利用多样化的AI提供商 aehrutktrjk 人工智能 langchain python
LangChain集成指南:如何利用多样化的AI提供商引言在人工智能和机器学习领域,LangChain已成为一个强大而灵活的框架,允许开发者轻松集成各种AI服务提供商。本文将深入探讨LangChain的集成能力,介绍如何利用不同的AI提供商来增强你的应用程序,并提供实用的代码示例。LangChain集成概览LangChain支持多种AI提供商的集成,这些集成可以分为两类:独立包集成:这些提供商有独
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏租房推荐系统 58同城租房爬虫房源推荐系统房价预测系统计算机毕业设计机器学习深度学习人工智能 2401_84572577 程序员大数据 hadoop 人工智能
做了那么多年开发，自学了很多门编程语言，我很明白学习资源对于学一门新语言的重要性，这些年也收藏了不少的Python干货，对我来说这些东西确实已经用不到了，但对于准备自学Python的人来说，或许它就是一个宝藏，可以给你省去很多的时间和精力。别在网上瞎学了，我最近也做了一些资源的更新，只要你是我的粉丝，这期福利你都可拿走。我先来介绍一下这些东西怎么用，文末抱走。（1）Python所有方向的学习路线（
【机器学习与R语言】1-机器学习简介苹果酱0567 面试题汇总与解析 java 中间件开发语言 spring boot 后端
1.基本概念机器学习：发明算法将数据转化为智能行为数据挖掘VS机器学习：前者侧重寻找有价值的信息，后者侧重执行已知的任务。后者是前者的先期准备过程：数据——>抽象化——>一般化。或者：收集数据——推理数据——归纳数据——发现规律抽象化：训练：用一个特定模型来拟合数据集的过程用方程来拟合观测的数据：观测现象——数据呈现——模型建立。通过不同的格式来把信息概念化一般化：一般化：将抽象化的知识转换成可用
Python前沿技术：机器学习与人工智能 4.0啊 Python 人工智能 python 机器学习
Python前沿技术：机器学习与人工智能一、引言随着科技的飞速发展，机器学习和人工智能（AI）已经成为了计算机科学领域的热门话题。Python作为一门易学易用且功能强大的编程语言，已经成为了这两个领域的首选语言之一。本文将深入探讨Python在机器学习和人工智能领域的应用，以及一些前沿技术和工具。二、Python机器学习基础2.1机器学习概述机器学习是人工智能（AI）的一个关键子集，它的核心在于让
chatgpt赋能python：如何在Python中计算平均值 tulingtest ChatGpt python chatgpt numpy 计算机
如何在Python中计算平均值计算平均值是数据分析、统计和机器学习等许多领域中的常见任务。Python作为一门功能强大且易于学习的编程语言，为计算平均值提供了多种方法。在本文中，我们将介绍如何在Python中计算平均值。什么是平均值简单来说，平均值是一组数字的总和除以数字的数量。例如，对于数字序列1，3，5，7，9，平均值是(1+3+5+7+9)/5=5。平均值在数据分析中非常有用，因为它可以提供
Python 初学者入门必知： Anaconda是什么？有什么作用？怎么使用？懒大王爱吃狼 Python基础 python 开发语言 python基础 python学习 anaconda anaconda安装 python教程
初学者在学习Python时，经常看到的一个名字是Anaconda。究竟什么是Anaconda，为什么它如此受欢迎？在这篇文章中，我们将探讨Anaconda，了解Anaconda的从安装到使用的。Anaconda是一个免费开源的Python和R编程发行版，包含上千个适用于数据科学和机器学习的包。同时，配备了Spyder和Jupyternotebook等工具，初学者可以使用它们来学习Python，使用
每天五分钟玩转深度学习PyTorch：模型参数优化器torch.optim 幻风_huanfeng 深度学习框架pytorch 深度学习 pytorch 人工智能神经网络机器学习优化算法
本文重点在机器学习或者深度学习中，我们需要通过修改参数使得损失函数最小化(或最大化)，优化算法就是一种调整模型参数更新的策略。在pytorch中定义了优化器optim，我们可以使用它调用封装好的优化算法，然后传递给它神经网络模型参数，就可以对模型进行优化。本文是学习第6步(优化器)，参考链接pytorch的学习路线随机梯度下降算法在深度学习和机器学习中，梯度下降算法是最常用的参数更新方法，它的公式
一切皆是映射：AI的去中心化：区块链技术的融合 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
一切皆是映射：AI的去中心化：区块链技术的融合作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming关键词：AI，区块链，去中心化，智能合约，共识机制，数据安全，隐私保护，分布式账本技术，机器学习，数据隐私1.背景介绍1.1问题的由来随着人工智能（AI）技术的快速发展，其在各个领域的应用越来越广泛，从自动驾驶、智能医疗到金融服务，AI正在改变着我们的生活。
第五届核磁机器学习班（训练营：2023.6.5~6.17）茗创科技
茗创科技专注于脑科学数据处理，涵盖（EEG/ERP,fMRI,结构像,DTI,ASL,FNIRS）等，欢迎留言讨论及转发推荐，也欢迎了解茗创科技的脑电课程，数据处理服务及脑科学工作站销售业务，可添加我们的工程师（微信号MCKJ-zhouyi或17373158786）咨询。★课程简介★基于血氧水平依赖的功能磁共振成像(fMRI)技术,利用其数据构建的功能性脑网络后,发现脑并不是一个单纯对外界刺激进行
如何有效的学习AI大模型？ Python程序员罗宾学习人工智能语言模型自然语言处理架构
学习AI大模型是一个系统性的过程，涉及到多个学科的知识。以下是一些建议，帮助你更有效地学习AI大模型：基础知识储备：数学基础：学习线性代数、概率论、统计学和微积分等，这些是理解机器学习算法的数学基础。编程技能：掌握至少一种编程语言，如Python，因为大多数AI模型都是用Python实现的。理论学习：机器学习基础：了解监督学习、非监督学习、强化学习等基本概念。深度学习：学习神经网络的基本结构，如卷
HQL之投影查询归来朝歌 HQL Hibernate 查询语句投影查询
在HQL查询中，常常面临这样一个场景，对于多表查询，是要将一个表的对象查出来还是要只需要每个表中的几个字段，最后放在一起显示？针对上面的场景，如果需要将一个对象查出来： HQL语句写“from 对象”即可 Session session = HibernateUtil.openSession();
Spring整合redis bylijinnan redis
pom.xml <dependencies>  <dependency> <groupId>org.springframework.data</groupId> <artifactId>spring-data-redi
org.hibernate.NonUniqueResultException: query did not return a unique result: 2 0624chenhong Hibernate
参考：http://blog.csdn.net/qingfeilee/article/details/7052736 org.hibernate.NonUniqueResultException: query did not return a unique result: 2 在项目中出现了org.hiber
android动画效果不懂事的小屁孩 android动画
前几天弄alertdialog和popupwindow的时候，用到了android的动画效果，今天专门研究了一下关于android的动画效果，列出来，方便以后使用。 Android 平台提供了两类动画。一类是Tween动画，就是对场景里的对象不断的进行图像变化来产生动画效果（旋转、平移、放缩和渐变）。第二类就是 Frame动画，即顺序的播放事先做好的图像，与gif图片原理类似。
js delete 删除机理以及它的内存泄露问题的解决方案换个号韩国红果果 JavaScript
delete删除属性时只是解除了属性与对象的绑定，故当属性值为一个对象时，删除时会造成内存泄露（其实还未删除）举例： var person={name:{firstname:'bob'}} var p=person.name delete person.name p.firstname -->'bob' // 依然可以访问p.firstname，存在内存泄露
Oracle将零干预分析加入网络即服务计划蓝儿唯美 oracle
由Oracle通信技术部门主导的演示项目并没有在本月较早前法国南斯举行的行业集团TM论坛大会中获得嘉奖。但是，Oracle通信官员解雇致力于打造一个支持零干预分配和编制功能的网络即服务（NaaS）平台，帮助企业以更灵活和更适合云的方式实现通信服务提供商（CSP）的连接产品。这个Oracle主导的项目属于TM Forum Live!活动上展示的Catalyst计划的19个项目之一。Catalyst计
spring学习——springmvc（二） a-john springMVC
Spring MVC提供了非常方便的文件上传功能。 1，配置Spring支持文件上传： DispatcherServlet本身并不知道如何处理multipart的表单数据，需要一个multipart解析器把POST请求的multipart数据中抽取出来，这样DispatcherServlet就能将其传递给我们的控制器了。为了在Spring中注册multipart解析器，需要声明一个实现了Mul
POJ-2828-Buy Tickets aijuans ACM_POJ
POJ-2828-Buy Tickets http://poj.org/problem?id=2828 线段树，逆序插入 #include<iostream>#include<cstdio>#include<cstring>#include<cstdlib>using namespace std;#define N 200010struct
Java Ant build.xml详解 asia007 build.xml
1,什么是antant是构建工具2,什么是构建概念到处可查到，形象来说，你要把代码从某个地方拿来，编译，再拷贝到某个地方去等等操作，当然不仅与此，但是主要用来干这个3,ant的好处跨平台 --因为ant是使用java实现的，所以它跨平台使用简单--与ant的兄弟make比起来语法清晰--同样是和make相比功能强大--ant能做的事情很多，可能你用了很久，你仍然不知道它能有
android按钮监听器的四种技术百合不是茶 android xml配置监听器实现接口
android开发中经常会用到各种各样的监听器,android监听器的写法与java又有不同的地方; 1,activity中使用内部类实现接口 ,创建内部类实例使用add方法与java类似创建监听器的实例 myLis lis = new myLis(); 使用add方法给按钮添加监听器
软件架构师不等同于资深程序员 bijian1013 程序员架构师架构设计
本文的作者Armel Nene是ETAPIX Global公司的首席架构师，他居住在伦敦，他参与过的开源项目包括 Apache Lucene,，Apache Nutch， Liferay 和 Pentaho等。如今很多的公司
TeamForge Wiki Syntax & CollabNet User Information Center sunjing TeamForge How do Attachement Anchor Wiki Syntax
the CollabNet user information center http://help.collab.net/ How do I create a new Wiki page? A CollabNet TeamForge project can have any number of Wiki pages. All Wiki pages are linked, and
【Redis四】Redis数据类型 bit1129 redis
概述 Redis是一个高性能的数据结构服务器，称之为数据结构服务器的原因是，它提供了丰富的数据类型以满足不同的应用场景，本文对Redis的数据类型以及对这些类型可能的操作进行总结。 Redis常用的数据类型包括string、set、list、hash以及sorted set.Redis本身是K/V系统，这里的数据类型指的是value的类型，而不是key的类型，key的类型只有一种即string
SSH2整合-附源码白糖_ eclipse spring tomcat Hibernate Google
今天用eclipse终于整合出了struts2+hibernate+spring框架。我创建的是tomcat项目，需要有tomcat插件。导入项目以后，鼠标右键选择属性，然后再找到“tomcat”项，勾选一下“Is a tomcat project”即可。具体方法见源码里的jsp图片，sql也在源码里。补充1：项目中部分jar包不是最新版的，可能导
[转]开源项目代码的学习方法 braveCS 学习方法
转自： http://blog.sina.com.cn/s/blog_693458530100lk5m.html http://www.cnblogs.com/west-link/archive/2011/06/07/2074466.html 1）阅读features。以此来搞清楚该项目有哪些特性2）思考。想想如果自己来做有这些features的项目该如何构架3）下载并安装d
编程之美-子数组的最大和（二维） bylijinnan 编程之美
package beautyOfCoding; import java.util.Arrays; import java.util.Random; public class MaxSubArraySum2 { /** * 编程之美子数组之和的最大值（二维） */ private static final int ROW = 5; private stat
读书笔记-3 chengxuyuancsdn jquery笔记 resultMap配置 ibatis一对多配置
1、resultMap配置 2、ibatis一对多配置 3、jquery笔记 1、resultMap配置当<select resultMap="topic_data"> <resultMap id="topic_data">必须一一对应。 (1)<resultMap class="tblTopic&q
[物理与天文]物理学新进展 comsci
如果我们必须获得某种地球上没有的矿石,才能够进行某些能量输出装置的设计和建造,而要获得这种矿石,又必须首先进行深空探测,而要进行深空探测,又必须获得这种能量输出装置,这个矛盾的循环,会导致地球联盟在与宇宙文明建立关系的时候,陷入困境怎么办呢?
Oracle 11g新特性:Automatic Diagnostic Repository daizj oracle ADR
Oracle Database 11g的FDI（Fault Diagnosability Infrastructure）是自动化诊断方面的又一增强。 FDI的一个关键组件是自动诊断库（Automatic Diagnostic Repository-ADR）。在oracle 11g中，alert文件的信息是以xml的文件格式存在的，另外提供了普通文本格式的alert文件。这两份log文
简单排序:选择排序 dieslrae 选择排序
public void selectSort(int[] array){ int select; for(int i=0;i<array.length;i++){ select = i; for(int k=i+1;k<array.leng
C语言学习六指针的经典程序，互换两个数字 dcj3sjt126com c
示例程序，swap_1和swap_2都是错误的，推理从1开始推到2，2没完成，推到3就完成了 # include <stdio.h> void swap_1(int, int); void swap_2(int *, int *); void swap_3(int *, int *); int main(void) { int a = 3; int b =
php 5.4中php-fpm 的重启、终止操作命令 dcj3sjt126com PHP
php 5.4中php-fpm 的重启、终止操作命令: 查看php运行目录命令：which php/usr/bin/php 查看php-fpm进程数：ps aux | grep -c php-fpm 查看运行内存/usr/bin/php -i|grep mem 重启php-fpm/etc/init.d/php-fpm restart 在phpinfo()输出内容可以看到php
线程同步工具类 shuizhaosi888 同步工具类
同步工具类包括信号量（Semaphore）、栅栏（barrier）、闭锁（CountDownLatch）闭锁（CountDownLatch） public class RunMain { public long timeTasks(int nThreads, final Runnable task) throws InterruptedException { fin
bleeding edge是什么意思 haojinghua DI
不止一次，看到很多讲技术的文章里面出现过这个词语。今天终于弄懂了——通过朋友给的浏览软件，上了wiki。我再一次感到，没有辞典能像WiKi一样，给出这样体贴人心、一清二楚的解释了。为了表达我对WiKi的喜爱，只好在此一一中英对照，给大家上次课。 In computer science, bleeding edge is a term that
c中实现utf8和gbk的互转 jimmee c iconv utf8&gbk编码
#include <iconv.h> #include <stdlib.h> #include <stdio.h> #include <unistd.h> #include <fcntl.h> #include <string.h> #include <sys/stat.h> int code_c
大型分布式网站架构设计与实践 lilin530 应用服务器搜索引擎
1.大型网站软件系统的特点？ a.高并发，大流量。 b.高可用。 c.海量数据。 d.用户分布广泛，网络情况复杂。 e.安全环境恶劣。 f.需求快速变更，发布频繁。 g.渐进式发展。 2.大型网站架构演化发展历程？ a.初始阶段的网站架构。应用程序，数据库，文件等所有的资源都在一台服务器上。 b.应用服务器和数据服务器分离。 c.使用缓存改善网站性能。 d.使用应用
在代码中获取Android theme中的attr属性值 OliveExcel android theme
Android的Theme是由各种attr组合而成, 每个attr对应了这个属性的一个引用, 这个引用又可以是各种东西. 在某些情况下, 我们需要获取非自定义的主题下某个属性的内容 (比如拿到系统默认的配色colorAccent), 操作方式举例一则: int defaultColor = 0xFF000000; int[] attrsArray = { andorid.r.
基于Zookeeper的分布式共享锁 roadrunners zookeeper 分布式共享锁
首先，说说我们的场景，订单服务是做成集群的，当两个以上结点同时收到一个相同订单的创建指令，这时并发就产生了，系统就会重复创建订单。等等......场景。这时，分布式共享锁就闪亮登场了。共享锁在同一个进程中是很容易实现的，但在跨进程或者在不同Server之间就不好实现了。Zookeeper就很容易实现。具体的实现原理官网和其它网站也有翻译，这里就不在赘述了。官
两个容易被忽略的MySQL知识 tomcat_oracle mysql
1、varchar(5)可以存储多少个汉字，多少个字母数字？　　相信有好多人应该跟我一样，对这个已经很熟悉了，根据经验我们能很快的做出决定，比如说用varchar(200)去存储url等等，但是，即使你用了很多次也很熟悉了，也有可能对上面的问题做出错误的回答。　　这个问题我查了好多资料，有的人说是可以存储5个字符，2.5个汉字（每个汉字占用两个字节的话），有的人说这个要区分版本，5.0
zoj 3827 Information Entropy(水题) 阿尔萨斯 format
题目链接：zoj 3827 Information Entropy 题目大意：三种底，计算和。解题思路：调用库函数就可以直接算了，不过要注意Pi = 0的时候，不过它题目里居然也讲了。。。limp→0+plogb(p)=0，因为p是logp的高阶。 #include <cstdio> #include <cstring> #include <cmath&

机器学习之HMM

你可能感兴趣的:(机器学习)