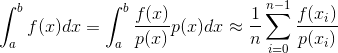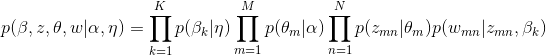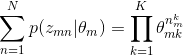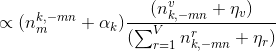liuy9803

机器学习主题模型之LDA参数求解——Gibbs采样

LDA参数推导的Gibbs采样方法基于马尔科夫链蒙特卡洛方法，因此首先学习MCMC方法。

一、马尔科夫链蒙特卡洛方法

MCMC（Markov Chain Monte Carlo）方法是构造适合的马尔科夫链，使其平稳分布为待估参数的后验分布，抽样并使用蒙特卡洛方法进行积分计算，实现了抽样分布随模拟的进行而改变的动态模拟，弥补了传统蒙特卡洛积分只能静态模拟的缺陷。

1、蒙特卡洛方法

蒙特卡洛方法是以概率统计的理论方法为基础的一种数值计算方法，将所要求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解，故又称随机抽样法或统计试验法。这种方法求得的是近似解，对于一些复杂问题往往是唯一可行的方法，模拟的样本数越大越接近真实值，但同时计算量也大幅上升。

蒙特卡洛方法的三个步骤：

（1）构造/描述概率过程

对于本身就具有随机性质的问题，如粒子运输问题，只要正确描述和模拟这个概率过程即可；对于本来不是随机性质的确定性问题，如定积分计算，就需要构造一个人为的概率过程，将不具有随机性质的问题转化为随机性质的问题。

例如要求f(x)在[a,b]上的积分，但原函数F(x)难以求解；如果可以得到x在[a,b]上的概率分布函数p(x)，则定积分可以近似求解为：

$\int_{a}^{b}f(x)dx=\int_{a}^{b}\frac{f(x)}{p(x)}p(x)dx\approx \frac{1}{n}\sum_{i=0}^{n-1}\frac{f(x_{i})}{p(x_{i})}$

（2）实现从已知概率分布中抽样

构造概率模型后，就可以基于概率分布去采样所需的n个x的样本集，带入求和式子即可求解。最基本的一个概率分布是(0,1)上的均匀分布，可以使用线性同余发生器LCG生成伪随机数样本：

x:=(a*x+c)%m, 00

对于一些常见的连续分布，如正态分布、t分布、F分布、Beta分布、 $\Gamma$ 分布等都可以通过uniform(0,1)的样本转换而得。

对于不是常见的分布，可以使用接受-拒绝采样来得到该分布的样本，即使用一个可以采样的分布q(x)与一个常数c相乘后，使得真实分布总在cq(x)曲线的下方。

重复以下步骤直到获得n个被接受的采样点：

①从cq(x)中获得一个随机采样点 $x_{0}$ ，值为 $cq(x_{0})$ ；

②计算接受概率acceptance probability： $\alpha =\frac{p(x_{0})}{cq(x_{0})}$ ；

③从uniform(0,1)中随机生成一个值u，如果ɑ≥u，则接受采样 $x_{0}$ ，否则拒绝 $x_{0}$ 并回到第一步。

从图上可以看出，cq(x)与p(x)曲线接近的地方接受概率较高，所以这样的地方采到的点就会比较多；而在接受概率较低的、差距较大的地方采到的点就会比较少，这也就保证了这个方法的有效性。

（3）建立各种估计量。

在构造了概率模型并从中抽样后，就可以确定一个随机变量，作为所要求问题的解——无偏估计。建立各种估计量，相当于对模拟实验的结果进行考察和登记，从中得到问题的解。

2、马尔科夫链

当后验分布的样本相互独立时，可以使用大数定律求解；当样本不独立时，就要使用马尔科夫链的平稳分布进行抽样。

对于一个非周期的马尔科夫链，任何两个状态i,j∈E是相通的（不可约），那么它的状态转移概率的极限存在且与i无关，则称此马尔科夫链具有遍历性： $\lim_{n\rightarrow \infty }p^{(n)}(i,j)=p_{j}$ ，此时若满足 $p_{j}\geqslant 0,\; \sum p_{j}=1$ ，则称 $p_{j}$ 为转移概率的极限分布。

平稳分布：若有限或无限数列 $\left \{ q_{j},j=1,2,... \right \}$ 满足 $q_{j}\geq 0,\; \sum q_{j}=1$ ，则称它是概率分布；如果此概率分布满足 $q_{j}=\sum_{i}^{ }q_{i}p(i,j)$ ，则称它是平稳分布。

有限马尔科夫链转移概率的极限分布一定是平稳分布；无限马尔科夫链转移概率的极限分布不一定是平稳分布。

在得到平稳分布的马尔科夫链状态转移矩阵后，就可以从这个平稳分布中采样蒙特卡洛方法所需的样本集了。

3、Metropolis-Hastings算法

对不满足细致平稳条件的马尔科夫链状态转移矩阵p，引入ɑ(i,j)使其可以取等号，即得到满足条件的目标矩阵P：

$q_{i}p(i,j)\neq q_{j}p(j,i)\\\\q_{i}p(i,j)\alpha (i,j)= q_{j}p(j,i)\alpha (j,i)\\\\\Rightarrow \left\{\begin{matrix} \alpha (i,j)=q_{j}p(j,i)\\ \alpha (j,i)=q_{i}p(i,j) \end{matrix}\right.\\\\\therefore P(i,j)=\alpha (i,j)\cdot p(i,j)$

ɑ(i,j)∈[0,1]称为接受率，P可以通过任意一个马尔科夫链状态转移矩阵p乘以ɑ(i,j)得到，注意每次转移后需要归一化矩阵使得每一行之和为1。但由于ɑ(i,j)可能非常小，导致大部分采样都被拒绝转移，马尔科夫链需要采样很多次才能收敛，采样效率很低。

MH采样将接受率做了如下改进，解决了接受率过低的问题：

$\alpha (i,j)=\min \left \{ \frac{q_{j}p(j,i)}{q_{i}p(i,j)},1 \right \}$

MH算法在特征很多的情况下，接受率的计算量很大；且在特征维度很高，难以求出特征的联合概率分布，只能得到特征之间的条件概率分布时，需要采取Gibbs采样的方法解决这类问题。

4、Gibbs Sampling

马尔科夫链通过转移概率矩阵可以收敛到稳定的概率分布，这意味着MCMC可以借助马尔科夫链的平稳分布特性模拟高维概率分布p(x)；当马尔科夫链经过burn-in阶段，消除初始参数的影响、达到平稳状态后，每一次状态转移都可以生成待模拟分布的一个样本。

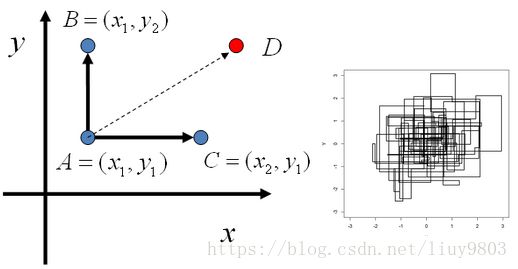
Gibbs采样是MCMC算法的一个特例，只对2维以上的情况有效，它交替随机固定某一维度，通过其他维度的值来抽样该维度的值。设p(x,y)是一个二维的联合概率分布，由下图可知：

$p(x_{1},y_{1})p(y_{2}|x_{1})=p(x_{1})p(y_{1}|x_{1})p(y_{2}|x_{1})=p(x_{1},y_{2})p(y_{1}|x_{1})$

$p(x_{1},y_{1})p(x_{2}|y_{1})=p(y_{1})p(x_{1}|y_{1})p(x_{2}|y_{1})=p(x_{2},y_{1})p(x_{1}|y_{1})$

$\Rightarrow \left\{\begin{matrix} p(A)p(y_{2}|x_{1})=p(B)p(y_{1}|x_{1})\\ p(A)p(x_{2}|y_{1})=p(C)p(x_{1}|y_{1}) \end{matrix}\right.$

所以在 $x=x_{1}$ 这条直线上，如果用条件概率分布 $p(y|x_{1})$ 作为马尔科夫链的状态转移概率，则任意两个点之间的转移满足细致平稳条件；在 $y=y_{1}$ 这条直线上也是如此。Gibbs采样和MH的不同之处在于，MH只是单独考虑某两个状态的采样（相当于直接从A到D），而Gibbs采样是沿着不同维度进行轮换采样的，且接受率ɑ=1 是MH算法的特例情况。最终的近似平稳分布可以通过采样结果 $\left \{(x_{n},y_{n}),(x_{n+1},y_{n+1}),... \right \}$ 近似表达。

二、Gibbs采样算法求解LDA思路

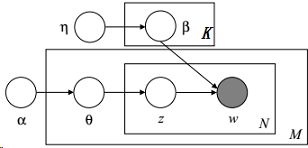
在Gibbs采样算法求解LDA的方法中，假设α、η是已知的先验输入，目的是推断隐变量的分布，即估计p(θ,z,β,w|ɑ,η)，可以通过对θ、β积分将它们边缘化去掉，这种方法称为collapse Gibbs sampling。

$p(\beta ,z,\theta ,w|\alpha ,\eta )=\prod_{k=1}^{K}p(\beta _{k}|\eta )\prod_{m=1}^{M}p(\theta _{m}|\alpha )\prod_{n=1}^{N}p(z_{mn}|\theta _{m})p(w_{mn}|z_{mn},\beta _{k})$

$p(z,w|\alpha ,\eta )\\\\=\int \int p(\theta ,z,w,\beta |\alpha ,\eta )d\theta d\beta \\\\=\int \prod_{m=1}^{M}p(\theta _{m}|\alpha )\prod_{n=1}^{N}p(z_{mn}|\theta_{m})d\mathbf{\theta}\cdot \int \prod_{k=1}^{K}p(\beta _{k}|\eta)\prod_{m=1}^{M}\prod_{n=1}^{N}p(w_{mn}|z_{mn},\beta_{k})d\beta$

假设每篇文档长度N相同，分别考虑θ、β这两部分的积分，令 $n_{n}^{k}$ 代表第m篇文档中分配给第k个主题的词的个数，对应的多项分布的计数为： $n_{m}=\left ( n_{m}^{1}, n_{m}^{2},..., n_{m}^{K} \right )$

$\sum_{n=1}^{N}p(z_{mn}|\theta _{m})=\prod_{k=1}^{K}\theta _{mk}^{n_{m}^{k}}$

先对θ部分进行计算，根据α→θ→z的Dir-Mult共轭分布关系，省略M的连乘可得：

$\int p(\theta _{m}|\alpha )\prod_{n=1}^{N}p(z_{mn}|\theta _{m})d\theta _{m}\\\\=\int \frac{\Gamma (\sum_{k=1}^{K}\alpha _{k})}{\prod_{k=1}^{K}\Gamma (\alpha _{k})}\prod_{k=1}^{K}\theta _{mk}^{\alpha _{k}-1}\prod_{k=1}^{K}\theta _{mk}^{n_{m}^{k}}d\theta _{m}\\\\=\int \frac{\Gamma (\sum_{k=1}^{K}\alpha _{k})}{\prod_{k=1}^{K}\Gamma (\alpha _{k})}\prod_{k=1}^{K}\theta _{mk}^{n_{m}^{k}+\alpha _{k}-1}d\theta _{m}$

根据Dirichlet分布的积分性质可知：

$\int \frac{\Gamma (\sum_{k=1}^{K}n_{m}^{k}+\alpha _{k})}{\prod_{k=1}^{K}\Gamma (n_{m}^{k}+\alpha _{k})}\prod_{k=1}^{K}\theta _{mk}^{n_{m}^{k}+\alpha _{k}-1}d\theta _{m}=1$

因此θ部分积分可化为：

$\int p(\theta _{m}|\alpha )\prod_{n=1}^{N}p(z_{mn}|\theta _{m})d\theta _{m}= \frac{\Gamma (\sum_{k=1}^{K}\alpha _{k})}{\prod_{k=1}^{K}\Gamma (\alpha _{k})}\cdot \frac{\prod_{k=1}^{K}\Gamma (n_{m}^{k}+\alpha _{k})}{\Gamma (\sum_{k=1}^{K}n_{m}^{k}+\alpha _{k})}$

同样地，令 $n_{k}^{v}$ 代表第k个主题对应词典中第v个词的词个数，对应的多项分布的计数为： $n_{k}=\left ( n_{k}^{1}, n_{k}^{2},..., n_{k}^{V} \right )$ ，可将β部分的积分写为：

$\int \prod_{k=1}^{K}p(\beta _{k}|\eta)\prod_{m=1}^{M}\prod_{n=1}^{N}p(w_{mn}|z_{mn},\beta_{k})d\beta \\\\=\prod_{k=1}^{K}\int p(\beta _{k}|\eta)\prod_{m=1}^{M}\prod_{n=1}^{N}p(w_{mn}|z_{mn},\beta_{k})d\beta_{k}\\\\=\prod_{k=1}^{K}\int \frac{\Gamma (\sum_{v=1}^{V}\eta_{v})}{\prod_{v=1}^{V}\Gamma (\eta_{v})}\prod_{v=1}^{V}\beta _{mk}^{n_{k}^{v}+\eta _{v}-1}d\beta _{k}\\\\=\prod_{k=1}^{K}\frac{\Gamma (\sum_{v=1}^{V}\eta_{v})}{\prod_{v=1}^{V}\Gamma (\eta_{v})}\cdot \frac{\prod_{v=1}^{V}\Gamma (n_{k}^{v}+\eta _{v})}{\Gamma (\sum_{v=1}^{V}n_{k}^{v}+\eta _{v})}$

最终得到主题和词的联合分布如下：

$p(z,w|\alpha ,\eta )=\prod_{m=1}^{M}\frac{\Gamma (\sum_{k=1}^{K}\alpha _{k})}{\prod_{k=1}^{K}\Gamma (\alpha _{k})}\cdot \frac{\prod_{k=1}^{K}\Gamma (n_{m}^{k}+\alpha _{k})}{\Gamma (\sum_{k=1}^{K}n_{m}^{k}+\alpha _{k})} \times \prod_{k=1}^{K}\frac{\Gamma (\sum_{v=1}^{V}\eta_{v})}{\prod_{v=1}^{V}\Gamma (\eta_{v})}\cdot \frac{\prod_{v=1}^{V}\Gamma (n_{k}^{v}+\eta _{v})}{\Gamma (\sum_{v=1}^{V}n_{k}^{v}+\eta _{v})}$

Gibbs采样的目标是接近分布p(z|w,ɑ,η)，由于w,ɑ,η已知，令 $z_{mn}$ 表示第m篇文档的第n个词对应的主题， $z_{-mn}$ 代表z去掉 $z_{mn}$ 后的主题分布。

$p(z_{mn}|z_{-mn},w,\alpha ,\eta )=\frac{p(z_{mn},z_{-mn},w|\alpha ,\eta)}{p(z_{-mn},w|\alpha ,\eta )}$

注意到Gibbs采样只需要为 $z_{mn}$ 采一个样，因此不用得到上式准确的值，只需得到 $z_{mn}$ 取值的比值即可，将上式简化为：

$p(z_{mn}=k|z_{-mn},w,\alpha ,\eta )\\\\\propto p(z_{mn}=k,z_{-mn},w|\alpha ,\eta )\\\\=\left ( \frac{\Gamma (\sum_{i=1}^{K}\alpha _{i})}{\prod_{i=1}^{K}\Gamma (\alpha _{i})} \right )^{M}\prod_{j\neq m}^{ }\frac{\prod_{i=1}^{K}\Gamma (n_{j}^{i}+\alpha _{i})}{\Gamma (\sum_{i=1}^{K}n_{j}^{i}+\alpha _{i})}\left ( \frac{\Gamma (\sum_{r=1}^{V}\eta _{r})}{\prod_{r=1}^{V}\Gamma (\eta _{r})} \right )^{K}\\\\\cdot \prod_{i=1}^{K}\prod_{r\neq v}^{ }\Gamma (n_{i}^{r}+\eta _{r})\frac{\prod_{i=1}^{K}\Gamma (n_{m}^{i}+\alpha _{i})}{\Gamma (\sum_{i=1}^{K}n_{m}^{i}+\alpha _{i})}\prod_{i=1}^{K}\frac{\Gamma (n_{i}^{v}+\eta _{v})}{\Gamma (\sum_{r=1}^{V}n_{i}^{r}+\eta _{r})}$

$\propto \prod_{i=1}^{K}\Gamma (n_{m}^{i}+\alpha _{i})\frac{\Gamma (n_{i}^{v}+\eta _{v})}{\Gamma (\sum_{r=1}^{V}n_{i}^{r}+\eta _{r})}$

$\propto \prod_{i\neq k}^{ }\Gamma (n_{m}^{i,-mn}+\alpha _{i})\frac{\Gamma (n_{i,-mn}^{v}+\eta _{v})}{\Gamma (\sum_{r=1}^{V}n_{i,-mn}^{r}+\eta _{r})}\cdot \Gamma (n_{m}^{k,-mn}+\alpha _{k}+1)\frac{\Gamma (n_{k,-mn}^{v}+\eta _{v}+1)}{\Gamma (\sum_{r=1}^{V}n_{k,-mn}^{r}+\eta _{r}+1)}$

$= \prod_{i}^{ }\Gamma (n_{m}^{i,-mn}+\alpha _{i})\frac{\Gamma (n_{i,-mn}^{v}+\eta _{v})}{\Gamma (\sum_{r=1}^{V}n_{i,-mn}^{r}+\eta _{r})}\cdot (n_{m}^{k,-mn}+\alpha _{k})\frac{ (n_{k,-mn}^{v}+\eta _{v})}{(\sum_{r=1}^{V}n_{k,-mn}^{r}+\eta _{r})}$

$\propto (n_{m}^{k,-mn}+\alpha _{k})\frac{ (n_{k,-mn}^{v}+\eta _{v})}{(\sum_{r=1}^{V}n_{k,-mn}^{r}+\eta _{r})}$

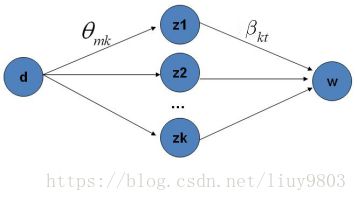
Gibbs采样公式的物理意义就是在K条doc→topic→word的路径中进行采样，当采样收敛后可得所有词最终的主题z，统计每篇文档中的主题概率p(topic|doc)可得文档主题分布 $\theta _{m}$ ，统计每个主题中所有的词概率p(word|topic)可得主题词分布 $\beta _{k}$ 。

三、LDA Gibbs采样算法流程总结

（1）选择适当的主题总数K，及LDA模型参数ɑ、η；

（2）对应文集中的每一篇文档的每个词w，随机赋予一个主题编号z；

（3）重新扫描文集，对每个词w使用Gibbs采样公式更新它的主题编号，并更新文集中的词；

（4）重复采样过程直至收敛；

（5）统计文集中topic-word共现频率矩阵，即可得到LDA模型。

通常训练LDA模型时，取Gibbs采样收敛之后的n个迭代的结果进行平均来做参数估计，这样模型质量更高。

当LDA模型训练好后，要确定一篇新文档的主题时，由于各个主题的词分布 $\beta _{k}$ 已经确定，只需要对 $\theta _{m}$ 进行采样计算即可。

选择适合的超参数K非常关键，对于简单的语义区分可选择较小的K，对于复杂的语义区分则选择较大的K，且需要足够多的语料。

Gibbs采样容易并行化，可以很方便的使用大数据平台来分布式地训练海量文档的LDA模型。

参考资料

https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation

lda数学八卦

https://blog.csdn.net/pipisorry/article/details/51373090

http://www.cnblogs.com/pinard/p/6831308.html

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
机器学习-聚类算法不良人龍木木机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
python中zeros用法_Python中的numpy.zeros()用法江平舟 python中zeros用法
numpy.zeros()函数是最重要的函数之一,广泛用于机器学习程序中。此函数用于生成包含零的数组。numpy.zeros()函数提供给定形状和类型的新数组,并用零填充。句法numpy.zeros(shape,dtype=float,order='C'参数形状：整数或整数元组此参数用于定义数组的尺寸。此参数用于我们要在其中创建数组的形状,例如(3,2)或2。dtype：数据类型(可选)此参数用于
【NumPy】深入解析numpy.zeros()函数二七830 numpy
欢迎莅临我的个人主页这里是我深耕Python编程、机器学习和自然语言处理（NLP）领域，并乐于分享知识与经验的小天地！博主简介：我是二七830，一名对技术充满热情的探索者。多年的Python编程和机器学习实践，使我深入理解了这些技术的核心原理，并能够在实际项目中灵活应用。尤其是在NLP领域，我积累了丰富的经验，能够处理各种复杂的自然语言任务。技术专长：我熟练掌握Python编程语言，并深入研究了机
【中国国际航空-注册_登录安全分析报告】风控牛验证码接口安全评测系列安全行为验证极验网易易盾智能手机
前言由于网站注册入口容易被黑客攻击，存在如下安全问题：1.暴力破解密码，造成用户信息泄露2.短信盗刷的安全问题，影响业务及导致用户投诉3.带来经济损失，尤其是后付费客户，风险巨大，造成亏损无底洞所以大部分网站及App都采取图形验证码或滑动验证码等交互解决方案，但在机器学习能力提高的当下，连百度这样的大厂都遭受攻击导致点名批评，图形验证及交互验证方式的安全性到底如何？请看具体分析一、中国国际航空PC
机器学习流形数据降维：UMAP 降维算法小嗷犬 Python 机器学习 #数据分析及可视化机器学习算法人工智能
✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。个人主页：小嗷犬的个人主页个人网站：小嗷犬的技术小站个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP（UniformManifoldApproximatio
七.正则化愿风去了
吴恩达机器学习之正则化（Regularization）http://www.cnblogs.com/jianxinzhou/p/4083921.html从数学公式上理解L1和L2https://blog.csdn.net/b876144622/article/details/81276818虽然在线性回归中加入基函数会使模型更加灵活，但是很容易引起数据的过拟合。例如将数据投影到30维的基函数上，模
机器学习-------数据标准化罔闻_spider 数据分析算法机器学习人工智能
什么是归一化，它与标准化的区别是什么？一作用在做训练时，需要先将特征值与标签标准化，可以防止梯度防炸和过拟合；将标签标准化后，网络预测出的数据是符合标准正态分布的—StandarScaler()，与真实值有很大差别。因为StandarScaler()对数据的处理是（真实值-平均值）/标准差。同时在做预测时需要将输出数据逆标准化提升模型精度：标准化/归一化使不同维度的特征在数值上更具比较性，提高分类
分享一个基于python的电子书数据采集与可视化分析 hadoop电子书数据分析与推荐系统 spark大数据毕设项目（源码、调试、LW、开题、PPT) 计算机源码社 Python项目大数据大数据 python hadoop 计算机毕业设计选题计算机毕业设计源码数据分析 spark毕设
作者：计算机源码社个人简介：本人八年开发经验，擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等，大家有这一块的问题可以一起交流！学习资料、程序开发、技术解答、文档报告如需要源码，可以扫取文章下方二维码联系咨询Java项目微信小程序项目Android项目Python项目PHP项目ASP.NET项目Node.js项目选题推荐项目实战|p
两种方法判断Python的位数是32位还是64位 sanqima Python编程电脑 python 开发语言
Python从1991年发布以来，凭借其简洁、清晰、易读的语法、丰富的标准库和第三方工具，在Web开发、自动化测试、人工智能、图形识别、机器学习等领域发展迅猛。 Python是一种胶水语言，通过Cython库与C/C++语言进行链接，通过Jython库与Java语言进行链接。 Python是跨平台的，可运行在多种操作系统上，包括但不限于Windows、Linux和macOS。这意味着用Py
使用最大边际相关性(MMR)选择示例：提高AI模型的多样性和相关性 aehrutktrjk 人工智能 easyui 前端 python
使用最大边际相关性(MMR)选择示例：提高AI模型的多样性和相关性引言在机器学习和自然语言处理领域，选择合适的训练示例对模型性能至关重要。最大边际相关性(MaximalMarginalRelevance,MMR)是一种优秀的示例选择方法，它不仅考虑了示例与输入的相关性，还注重保持所选示例之间的多样性。本文将深入探讨如何使用MMR来选择示例，以提高AI模型的性能和泛化能力。什么是最大边际相关性(MM
LangChain集成指南:如何利用多样化的AI提供商 aehrutktrjk 人工智能 langchain python
LangChain集成指南:如何利用多样化的AI提供商引言在人工智能和机器学习领域,LangChain已成为一个强大而灵活的框架,允许开发者轻松集成各种AI服务提供商。本文将深入探讨LangChain的集成能力,介绍如何利用不同的AI提供商来增强你的应用程序,并提供实用的代码示例。LangChain集成概览LangChain支持多种AI提供商的集成,这些集成可以分为两类:独立包集成:这些提供商有独
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏租房推荐系统 58同城租房爬虫房源推荐系统房价预测系统计算机毕业设计机器学习深度学习人工智能 2401_84572577 程序员大数据 hadoop 人工智能
做了那么多年开发，自学了很多门编程语言，我很明白学习资源对于学一门新语言的重要性，这些年也收藏了不少的Python干货，对我来说这些东西确实已经用不到了，但对于准备自学Python的人来说，或许它就是一个宝藏，可以给你省去很多的时间和精力。别在网上瞎学了，我最近也做了一些资源的更新，只要你是我的粉丝，这期福利你都可拿走。我先来介绍一下这些东西怎么用，文末抱走。（1）Python所有方向的学习路线（
【机器学习与R语言】1-机器学习简介苹果酱0567 面试题汇总与解析 java 中间件开发语言 spring boot 后端
1.基本概念机器学习：发明算法将数据转化为智能行为数据挖掘VS机器学习：前者侧重寻找有价值的信息，后者侧重执行已知的任务。后者是前者的先期准备过程：数据——>抽象化——>一般化。或者：收集数据——推理数据——归纳数据——发现规律抽象化：训练：用一个特定模型来拟合数据集的过程用方程来拟合观测的数据：观测现象——数据呈现——模型建立。通过不同的格式来把信息概念化一般化：一般化：将抽象化的知识转换成可用
Python前沿技术：机器学习与人工智能 4.0啊 Python 人工智能 python 机器学习
Python前沿技术：机器学习与人工智能一、引言随着科技的飞速发展，机器学习和人工智能（AI）已经成为了计算机科学领域的热门话题。Python作为一门易学易用且功能强大的编程语言，已经成为了这两个领域的首选语言之一。本文将深入探讨Python在机器学习和人工智能领域的应用，以及一些前沿技术和工具。二、Python机器学习基础2.1机器学习概述机器学习是人工智能（AI）的一个关键子集，它的核心在于让
chatgpt赋能python：如何在Python中计算平均值 tulingtest ChatGpt python chatgpt numpy 计算机
如何在Python中计算平均值计算平均值是数据分析、统计和机器学习等许多领域中的常见任务。Python作为一门功能强大且易于学习的编程语言，为计算平均值提供了多种方法。在本文中，我们将介绍如何在Python中计算平均值。什么是平均值简单来说，平均值是一组数字的总和除以数字的数量。例如，对于数字序列1，3，5，7，9，平均值是(1+3+5+7+9)/5=5。平均值在数据分析中非常有用，因为它可以提供
Python 初学者入门必知： Anaconda是什么？有什么作用？怎么使用？懒大王爱吃狼 Python基础 python 开发语言 python基础 python学习 anaconda anaconda安装 python教程
初学者在学习Python时，经常看到的一个名字是Anaconda。究竟什么是Anaconda，为什么它如此受欢迎？在这篇文章中，我们将探讨Anaconda，了解Anaconda的从安装到使用的。Anaconda是一个免费开源的Python和R编程发行版，包含上千个适用于数据科学和机器学习的包。同时，配备了Spyder和Jupyternotebook等工具，初学者可以使用它们来学习Python，使用
每天五分钟玩转深度学习PyTorch：模型参数优化器torch.optim 幻风_huanfeng 深度学习框架pytorch 深度学习 pytorch 人工智能神经网络机器学习优化算法
本文重点在机器学习或者深度学习中，我们需要通过修改参数使得损失函数最小化(或最大化)，优化算法就是一种调整模型参数更新的策略。在pytorch中定义了优化器optim，我们可以使用它调用封装好的优化算法，然后传递给它神经网络模型参数，就可以对模型进行优化。本文是学习第6步(优化器)，参考链接pytorch的学习路线随机梯度下降算法在深度学习和机器学习中，梯度下降算法是最常用的参数更新方法，它的公式
一切皆是映射：AI的去中心化：区块链技术的融合 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
一切皆是映射：AI的去中心化：区块链技术的融合作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming关键词：AI，区块链，去中心化，智能合约，共识机制，数据安全，隐私保护，分布式账本技术，机器学习，数据隐私1.背景介绍1.1问题的由来随着人工智能（AI）技术的快速发展，其在各个领域的应用越来越广泛，从自动驾驶、智能医疗到金融服务，AI正在改变着我们的生活。
第五届核磁机器学习班（训练营：2023.6.5~6.17）茗创科技
茗创科技专注于脑科学数据处理，涵盖（EEG/ERP,fMRI,结构像,DTI,ASL,FNIRS）等，欢迎留言讨论及转发推荐，也欢迎了解茗创科技的脑电课程，数据处理服务及脑科学工作站销售业务，可添加我们的工程师（微信号MCKJ-zhouyi或17373158786）咨询。★课程简介★基于血氧水平依赖的功能磁共振成像(fMRI)技术,利用其数据构建的功能性脑网络后,发现脑并不是一个单纯对外界刺激进行
如何有效的学习AI大模型？ Python程序员罗宾学习人工智能语言模型自然语言处理架构
学习AI大模型是一个系统性的过程，涉及到多个学科的知识。以下是一些建议，帮助你更有效地学习AI大模型：基础知识储备：数学基础：学习线性代数、概率论、统计学和微积分等，这些是理解机器学习算法的数学基础。编程技能：掌握至少一种编程语言，如Python，因为大多数AI模型都是用Python实现的。理论学习：机器学习基础：了解监督学习、非监督学习、强化学习等基本概念。深度学习：学习神经网络的基本结构，如卷
多线程编程之卫生间周凡杨 java 并发卫生间线程厕所
如大家所知，火车上车厢的卫生间很小，每次只能容纳一个人，一个车厢只有一个卫生间，这个卫生间会被多个人同时使用，在实际使用时，当一个人进入卫生间时则会把卫生间锁上，等出来时打开门，下一个人进去把门锁上，如果有一个人在卫生间内部则别人的人发现门是锁的则只能在外面等待。问题分析：首先问题中有两个实体，一个是人，一个是厕所，所以设计程序时就可以设计两个类。人是多数的，厕所只有一个（暂且模拟的是一个车厢）。
How to Install GUI to Centos Minimal sunjing linux Install Desktop GUI
http://www.namhuy.net/475/how-to-install-gui-to-centos-minimal.html I have centos 6.3 minimal running as web server. I’m looking to install gui to my server to vnc to my server. You can insta
Shell 函数 daizj shell 函数
Shell 函数 linux shell 可以用户定义函数，然后在shell脚本中可以随便调用。 shell中函数的定义格式如下： [function] funname [()]{ action; [return int;] } 说明： 1、可以带function fun() 定义，也可以直接fun() 定义,不带任何参数。 2、参数返回
Linux服务器新手操作之一周凡杨 Linux 简单操作
1.whoami 当一个用户登录Linux系统之后，也许他想知道自己是发哪个用户登录的。此时可以使用whoami命令。 [ecuser@HA5-DZ05 ~]$ whoami e
浅谈Socket通信（一）朱辉辉33 socket
在java中ServerSocket用于服务器端，用来监听端口。通过服务器监听，客户端发送请求，双方建立链接后才能通信。当服务器和客户端建立链接后，两边都会产生一个Socket实例，我们可以通过操作Socket来建立通信。首先我建立一个ServerSocket对象。当然要导入java.net.ServerSocket包 ServerSock
关于框架的简单认识西蜀石兰框架
入职两个月多，依然是一个不会写代码的小白，每天的工作就是看代码，写wiki。前端接触CSS、HTML、JS等语言，一直在用的CS模型，自然免不了数据库的链接及使用，真心涉及框架，项目中用到的BootStrap算一个吧，哦，JQuery只能算半个框架吧，我更觉得它是另外一种语言。后台一直是纯Java代码，涉及的框架是Quzrtz和log4j。都说学前端的要知道三大框架，目前node.
You have an error in your SQL syntax; check the manual that corresponds to your 林鹤霄
You have an error in your SQL syntax; check the manual that corresponds to your MySQL server version for the right syntax to use near 'option,changed_ids ) values('0ac91f167f754c8cbac00e9e3dc372
MySQL5.6的my.ini配置 aigo mysql
注意：以下配置的服务器硬件是：8核16G内存 [client] port=3306 [mysql] default-character-set=utf8 [mysqld] port=3306 basedir=D:/mysql-5.6.21-win
mysql 全文模糊查找便捷解决方案 alxw4616 mysql
mysql 全文模糊查找便捷解决方案 2013/6/14 by 半仙 [email protected] 目的: 项目需求实现模糊查找. 原则: 查询不能超过 1秒. 问题: 目标表中有超过1千万条记录. 使用like '%str%' 进行模糊查询无法达到性能需求. 解决方案: 使用mysql全文索引. 1.全文索引 : MySQL支持全文索引和搜索功能。MySQL中的全文索
自定义数据结构链表(单项 ,双向,环形) 百合不是茶单项链表双向链表
链表与动态数组的实现方式差不多, 数组适合快速删除某个元素链表则可以快速的保存数组并且可以是不连续的单项链表;数据从第一个指向最后一个实现代码: //定义动态链表 clas
threadLocal实例 bijian1013 java thread java多线程 threadLocal
实例1： package com.bijian.thread; public class MyThread extends Thread { private static ThreadLocal tl = new ThreadLocal() { protected synchronized Object initialValue() { return new Inte
activemq安全设置—设置admin的用户名和密码 bijian1013 java activemq
ActiveMQ使用的是jetty服务器, 打开conf/jetty.xml文件，找到 <bean id="adminSecurityConstraint" class="org.eclipse.jetty.util.security.Constraint"> <p
【Java范型一】Java范型详解之范型集合和自定义范型类 bit1129 java
本文详细介绍Java的范型，写一篇关于范型的博客原因有两个，前几天要写个范型方法(返回值根据传入的类型而定)，竟然想了半天，最后还是从网上找了个范型方法的写法；再者，前一段时间在看Gson, Gson这个JSON包的精华就在于对范型的优雅简单的处理，看它的源代码就比较迷糊，只其然不知其所以然。所以，还是花点时间系统的整理总结下范型吧。范型内容范型集合类范型类
【HBase十二】HFile存储的是一个列族的数据 bit1129 hbase
在HBase中，每个HFile存储的是一个表中一个列族的数据，也就是说，当一个表中有多个列簇时，针对每个列簇插入数据，最后产生的数据是多个HFile，每个对应一个列族，通过如下操作验证 1. 建立一个有两个列族的表 create 'members','colfam1','colfam2' 2. 在members表中的colfam1中插入50*5
Nginx 官方一个配置实例 ronin47 nginx 配置实例
user www www; worker_processes 5; error_log logs/error.log; pid logs/nginx.pid; worker_rlimit_nofile 8192; events { worker_connections 4096;} http { include conf/mim
java-15.输入一颗二元查找树，将该树转换为它的镜像，即在转换后的二元查找树中，左子树的结点都大于右子树的结点。用递归和循环 bylijinnan java
//use recursion public static void mirrorHelp1(Node node){ if(node==null)return; swapChild(node); mirrorHelp1(node.getLeft()); mirrorHelp1(node.getRight()); } //use no recursion bu
返回null还是empty bylijinnan java apache spring 编程
第一个问题，函数是应当返回null还是长度为0的数组（或集合）？第二个问题，函数输入参数不当时，是异常还是返回null？先看第一个问题有两个约定我觉得应当遵守： 1.返回零长度的数组或集合而不是null（详见《Effective Java》）理由就是，如果返回empty，就可以少了很多not-null判断： List<Person> list
[科技与项目]工作流厂商的战略机遇期 comsci 工作流
在新的战略平衡形成之前，这里有一个短暂的战略机遇期，只有大概最短6年，最长14年的时间，这段时间就好像我们森林里面的小动物，在秋天中，必须抓紧一切时间存储坚果一样，否则无法熬过漫长的冬季。。。。在微软，甲骨文，谷歌，IBM,SONY
过度设计-举例 cuityang 过度设计
过度设计，需要更多设计时间和测试成本，如无必要，还是尽量简洁一些好。未来的事情，比如访问量，比如数据库的容量，比如是否需要改成分布式都是无法预料的再举一个例子，对闰年的判断逻辑：　　1、 if($Year%4==0) return True; else return Fasle; 　　2、if ( ($Year%4==0 &am
java进阶，《Java性能优化权威指南》试读 darkblue086 java性能优化
记得当年随意读了微软出版社的.NET 2.0应用程序调试，才发现调试器如此强大，应用程序开发调试其实真的简单了很多，不仅仅是因为里面介绍了很多调试器工具的使用，更是因为里面寻找问题并重现问题的思想让我震撼，时隔多年，Java已经如日中天，成为许多大型企业应用的首选，而今天，这本《Java性能优化权威指南》让我再次找到了这种感觉，从不经意的开发过程让我刮目相看，原来性能调优不是简单地看看热点在哪里，
网络学习笔记初识OSI七层模型与TCP协议 dcj3sjt126com 学习笔记
协议：在计算机网络中通信各方面所达成的、共同遵守和执行的一系列约定　　计算机网络的体系结构：计算机网络的层次结构和各层协议的集合。　　两类服务：　　面向连接的服务通信双方在通信之前先建立某种状态，并在通信过程中维持这种状态的变化，同时为服务对象预先分配一定的资源。这种服务叫做面向连接的服务。　　面向无连接的服务通信双方在通信前后不建立和维持状态，不为服务对象
mac中用命令行运行mysql dcj3sjt126com mysql linux mac
参考这篇博客：http://www.cnblogs.com/macro-cheng/archive/2011/10/25/mysql-001.html 感觉workbench不好用（有点先入为主了）。 1，安装mysql 在mysql的官方网站下载 mysql 5.5.23 http://www.mysql.com/downloads/mysql/，根据我的机器的配置情况选择了64
MongDB查询（1）——基本查询[五] eksliang mongodb mongodb 查询 mongodb find
MongDB查询转载请出自出处：http://eksliang.iteye.com/blog/2174452 一、find简介 MongoDB中使用find来进行查询。 API:如下 function ( query , fields , limit , skip, batchSize, options ){.....} 参数含义： query:查询参数 fie
base64，加密解密经融加密，对接 y806839048 经融加密对接
String data0 = new String(Base64.encode(bo.getPaymentResult().getBytes(("GBK")))); String data1 = new String(Base64.decode(data0.toCharArray()),"GBK"); // 注意编码格式，注意用于加密，解密的要是同
JavaWeb之JSP概述 ihuning javaweb
什么是JSP？为什么使用JSP？ JSP表示Java Server Page，即嵌有Java代码的HTML页面。使用JSP是因为在HTML中嵌入Java代码比在Java代码中拼接字符串更容易、更方便和更高效。 JSP起源在很多动态网页中，绝大部分内容都是固定不变的，只有局部内容需要动态产生和改变。如果使用Servl
apple watch 指南啸笑天 apple
1. 文档 WatchKit Programming Guide（中译在线版 By @CocoaChina）译文译者原文概览 - 开始为 Apple Watch 进行开发 @星夜暮晨 Overview - Developing for Apple Watch 概览 - 配置 Xcode 项目 - Overview - Configuring Yo
java经典的基础题目 macroli java 编程
1.列举出 10个JAVA语言的优势 a:免费，开源，跨平台(平台独立性)，简单易用，功能完善，面向对象，健壮性，多线程，结构中立，企业应用的成熟平台, 无线应用 2.列举出JAVA中10个面向对象编程的术语 a:包，类，接口，对象，属性，方法，构造器，继承，封装，多态，抽象，范型 3.列举出JAVA中6个比较常用的包 Java.lang;java.util;java.io;java.sql;ja
你所不知道神奇的js replace正则表达式 qiaolevip 每天进步一点点学习永无止境纵观千象 regex
var v = 'C9CFBAA3CAD0'; console.log(v); var arr = v.split(''); for (var i = 0; i < arr.length; i ++) { if (i % 2 == 0) arr[i] = '%' + arr[i]; } console.log(arr.join('')); console.log(v.r
[一起学Hive]之十五-分析Hive表和分区的统计信息(Statistics) superlxw1234 hive hive分析表 hive统计信息 hive Statistics
关键字：Hive统计信息、分析Hive表、Hive Statistics 类似于Oracle的分析表，Hive中也提供了分析表和分区的功能，通过自动和手动分析Hive表，将Hive表的一些统计信息存储到元数据中。表和分区的统计信息主要包括：行数、文件数、原始数据大小、所占存储大小、最后一次操作时间等； 14.1 新表的统计信息对于一个新创建
Spring Boot 1.2.5 发布 wiselyman spring boot
Spring Boot 1.2.5已在7月2日发布，现在可以从spring的maven库和maven中心库下载。这个版本是一个维护的发布版，主要是一些修复以及将Spring的依赖提升至4.1.7(包含重要的安全修复)。官方建议所有的Spring Boot用户升级这个版本。项目首页 | 源

机器学习主题模型之LDA参数求解——Gibbs采样

你可能感兴趣的:(机器学习)