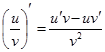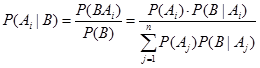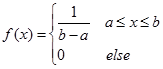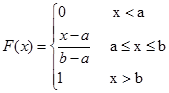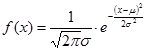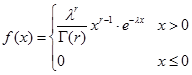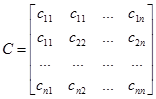机器学习之数学基础

机器学习之数学基础

一、常见导数

  
        

        

        

和差积商求导法则：      

复合函数：   

多变量函数 求偏导，即只有某一个自变量变化，固定其他自变量（看做常量）：

  

梯度：函数的梯度是一个向量，它的方向与取得最大方向导数的方向一致，模为方向导数的最大值。

  

二、Taylor公式

Taylor公式是用一个函数在某点的信息描述其附近取值的公式，如果函数足够平滑，在已知函数在某一点各阶导数值的情况下可以构建一个（高次）多项式近似表示函数在这一点的邻域中的值，同时给出误差公式。若函数f(x)在x₀的某个开区间(a,b)内有直到(n+1)阶导数，则对 ，有：

其中R_n(x)为Taylor公式的余项，Lagrange余项为：

x₀=0时为Maclaurin公式，为Taylor公式的特殊形式。

Taylor公式可用于求解近似值、极限值、积分敛散性、函数凹凸性/拐点、行列式计算等复杂数学问题，如 ；还可用于解释Gini系数、求交叉熵近似值、牛顿迭代法求近似平方根、XGBoost二阶Taylor展开公式等。

三、Lagrange乘数法

在数学最优问题中，寻求变量受一个或多个条件所限制的多元函数极值的方法。例如要寻找二元函数 在条件 下的可能极值点，先构造拉格朗日函数 ，λ为某一常数：

解方程组求出 ，则 就有可能是极值点的坐标。

推广到多个自变量的情况：

求函数 在条件 ， 下的极值，构造函数 ， 为常数，可由各个偏导 ， 解出可能的极值点坐标 。

四、向量与矩阵的运算

两个向量 ，夹角为 ；

矩阵 ，

1）向量加减

2）向量数乘

3）数量积

4）向量积

5）矩阵加减 A,B为同型矩阵

6）矩阵数乘

7）矩阵乘法

Numpy求矩阵的乘法

A*B即np.multiply(ndarray,ndarray)：矩阵对应位置的元素相乘

np.dot(ndarray,ndarray)或ndarray.dot(ndarray)：一个矩阵的行数与另一个列数相同

不同维度矩阵的乘法，如二维矩阵 与三维矩阵 相乘：A[:,:,None]*B。

8）矩阵转置

运算性质： ； ； ；

9）矩阵的逆

运算性质： ；   ；   

A、B同阶可逆，有 ；  

行列式 ，其中 为的代数余子式。行列式可以看做有向面积/体积在一般Euclid空间中的推广，行列式描述的是在n维Euclid空间中，一个线性变换对面积/体积所造成的的影响（比例）。

可逆矩阵（ ）为方阵、非奇异矩阵，行等价于单位矩阵，齐次线性方程组Ax=0只有零解；若矩阵A可逆，则它的逆矩阵是唯一的，满足消去律 。

numpy中求方阵的逆矩阵：np.linalg.inv(ndarray)。

伪逆矩阵是逆矩阵的广义形式，对于奇异矩阵或非方阵的矩阵可以用np.linalg.pinv(ndarray) 伪逆求矩阵的广义逆矩阵。

五、特征值、特征向量

A为n阶方阵，若数λ与n维非零列向量x满足Ax=λx,则称λ为A的特征值，x为对应于λ的特征向量。若A的所有特征根 ，则有性质：

在一个定义了内积的线性空间里，对一个n阶对称方阵进行特征分解，就是产生了该空间的n个标准正交基（特征向量），然后把矩阵投影到这n个基上，特征值的模代表矩阵在每个基上的投影长度。

应用：二次型最优化问题；数据降维——删除小特征值对应方向的数据。

设A为实对称矩阵，若二次型 是正定的，则称A为正定矩阵。考虑矩阵的特征值，若所有特征值均不小于0——半正定，若所有特征值均大于0——正定。

六、矩阵分解

矩阵分解是将矩阵拆解为数个矩阵的乘积，可分为三角分解、满秩分解、Jordan分解、QR分解和奇异值分解SVD等。

1、QR分解

将矩阵分解为一个正交矩阵与一个上三角形矩阵的乘积

求解步骤：

1）将m×n的矩阵写成n个m×1的列向量；

2）将列向量按照施密特正交化方法计算得到正交矩阵Q；

3）得出矩阵的QR分解

2、SVD分解

与特征值分解（方阵）类似，都是为了提取矩阵的重要特征，SVD适用于任意矩阵 其中U为m×m阶酉矩阵，Σ为半正定m×n阶对角矩阵，将奇异值由大到小排列即Σ可唯一确定，V^T为V的共轭转置矩阵 n×n阶酉矩阵。

七、向量与矩阵的求导

1、向量的导数

A为m×n的矩阵，x为n×1的列向量，则Ax为m×1的列向量：

2、标量对向量的导数

A为n×n的方阵，x为n×1的列向量，则x^TAx为标量：

若A为对称阵，则

3、标量对方阵的导数

A为n×n的方阵，|A|为A的行列式，求 ：

，   

八、排列组合与概率

1、排列数

从m个不同元素中取出n 个元素，并按照一定的顺序排成一列，称为从m个不同元素中取出n个元素的一个排列，记作：

2、组合数

从m个不同元素中取出n 个元素的所有组合的个数，称为从m个不同元素取出n个元素的组合数，记作：

3、古典概率

也称事前概率，即假定随机现象所能发生的事件是有限的、互不相容的，且每个基本事件发生的可能性相等。一般地，如果在全部可能出现的基本事件范围内构成事件A的基本事件有a个，不构成事件A的基本事件有b个，则事件A出现的概率为

4、联合概率

两个事件共同发生的概率，记作P(AB)、P(A,B)或P(A∩B)

5、条件概率

事件A在另外一个事件B已经发生的条件下发生的概率，一般，条件概率与联合概率的关系： ；推广到任意有穷多个事件时：

6、全概率公式

样本空间Ω有一组事件A₁, A₂, …, A_n，若事件组满足下面2个条件，则称事件组为样本空间的一个划分：

， ，

设事件{A_i}是样本空间的一个划分，且P(A_i)>0，则对任意事件B，全概率公式为：

7、贝叶斯公式

当不能准确知悉一个事物的本质时，可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。

设事件组A₁, A₂, …, A_n是样本空间Ω的一个划分，若对任意事件B有P(B)>0，则：

P(A)：在没有数据支持下，A发生的概率——先验/边缘概率

P(A|B)：在已知B发生后，A发生的条件概率——A的后验概率

九、离散型随机变量及其分布律

随机变量：随机试验的每一个结果都对应着变量X的一个确定的取值，则X是样本空间上的函数X=X(e) eϵS。若随机变量X的取值是有限个或可列无穷个，则称X为离散型随机变量。

常用的离散型随机变量分布：

1、Bernoulli分布（0-1分布/两点分布）

2、二项分布（n重Bernoulli分布）

3、Poisson分布

为常数

Poisson定理：若 ，当n比较大，p比较小时，令 ，则有：

4、几何分布

5、超几何分布

十、连续型随机变量及其概率密度

若对随机变量X的分布函数F(x)，存在非负函数f(x)，使对于任意实数x有： ，则称X为连续型随机变量，f(x)称为X的概率密度函数。若f(x)在x₀点连续，则 。

性质：

注意：概率密度不是概率，关心某点的取值并无太大意义，需要关注的是在某个区间上的取值。

常用的连续性随机变量分布：

1、均匀分布

  

2、指数分布 （ 为常数）

  

3、正态分布（高斯分布）

大量随机现象都是服从或近似服从正态分布的，所以一个随机指标受到诸多因素影响，但其中任何一个随机指标都不起决定性作用，则该随机指标服从或近似服从正态分布，正态分布可作为许多分布的近似分布。

)   

标准正态分布：

时：可以查表得到标准正态分布近似值

  

正态分布图形性质：

1）曲线关于 对称，对任意的h>0，有：

2）x离μ越远，f(x)的值就越小，即对同样长度的区间，当区间离μ越远时，x落在该区间中的概率就越小。当 时，f(x)取到最大值： 。

3）曲线y=f(x)在 处有拐点，以x轴为渐近线。

4）固定σ值，改变μ值，则曲线y=f(x)沿着x轴平行移动，不改变形状，即曲线y=f(x)的位置完全由μ所决定。

5）固定μ值，改变σ值，当σ越小时曲线y=f(x)的图形越陡，即x落在μ的附近的概率越大；反之当σ越大时，y=f(x)的图形越平坦，x的取值就越分散。

4、 -分布

  

函数性质：

若n为自然数，则

十一、数字特征

1、数学期望Mean

即均值，是概率加权下的平均值，为每次可能的结构的概率乘以其结果的总和，反映的是随机变量平均取值的大小，常用符号μ表示。

连续性随机变量的期望：

离散型随机变量的期望：

数学期望的性质：

E(C)=C E(CX)=CE(X) E(X+Y)=E(X)+E(Y)

若X与Y相互独立，E(XY)=E(X)E(Y)

2、方差Variance、标准差Standard Deviation

方差是衡量随机变量离散程度的度量，用来度量随机变量和它的数学期望之间的偏离程度。标准差σ是方差的算术平方根。

连续性随机变量的方差：

离散型随机变量的方差：

方差的性质：

D(C)=0   D(CX)=C2D(X)   D(C+X)=D(X)

若X,Y不相关，则

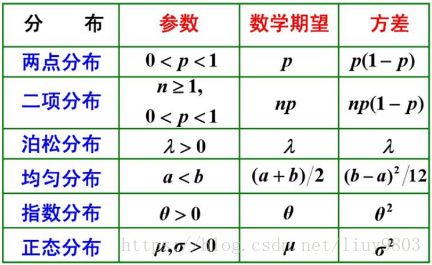
常见分布的数学期望和方差：

3、协方差Covariance

协方差常用于衡量两个变量的总体误差，方差是协方差的特殊情况，即两个变量相同的情况。

协方差是两个随机变量变化趋势的度量：

，则X与Y的变化趋势相同；

，则X与Y的变化趋势相反；

，则X与Y没有相关性。

性质：

协方差矩阵：

对于n个随机向量(X₁,X₂,…,X_n)，任意两个元素x_i，x_j都可得到一个协方差，从而形成一个n×n的矩阵，即协方差矩阵，这个协方差矩阵是对称的矩阵。

C中主对角线上的元素为方差

十二、大数定律、中心极限定理

1、大数定律（Law of Large Numbers）

随着样本容量n的增加，样本平均数将接近于总体平均数（期望μ），即可以使用一部分样本的平均值来代替整体样本的期望/均值，出现偏差的可能性是存在的，但当n足够大时，偏差趋近于0。

2、中心极限定理（Central Limit Theorem）

在独立同分布情况下，抽样样本的规范和在总体数量趋于无穷时的极限分布近似于正态分布。假设{X_n}为独立同分布的随机变量，并且具有相同的数学期望μ和方差σ²，则{X_n}服从中心极限定理，Z_n为{X_n}的规范和：

LLN与CLT关系？

中心极限定理：无论抽样分布如何，均值服从正态分布；而大数定律根本和正态分布无关，是说样本量大了抽样分布近似总体分布。

十三、最大似然估计

在总体的分布类型已知的条件下所使用的已知参数估计方法，基本思想是：当从模型总体随机抽取n组样本观测值后，最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大（寻找一个θ值使这个采样的可能性最大化）。

求解步骤：

1）写出似然函数

X为离散型：

X为连续型：

2）对似然函数两边取对数

X为离散型：

X为连续型：

3）求导并令之等于0

解对数似然方程： ，即可求出参数 的最大似然估计值 。

例如：

给定一组样本{X_n}，已知样本符合高斯分布 ，试估计μ和σ的值。

高斯分布的概率密度函数为：

①最大似然函数为：
②取对数：

③要求似然函数l(x)最大，即分别对μ和σ求导并解方程：