Pytorch实现二分类器

以下我们用 PyTorch 实现一个很简单的二分类器，所用的数据来自 Scikit learn。

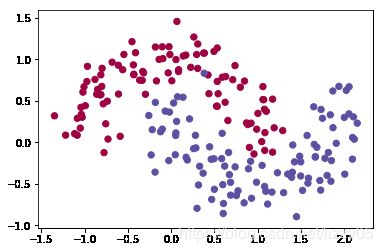
首先来生成含200个样本的数据，并绘制出样本的散点图如下图所示：

import matplotlib.pyplot as plt
from sklearn.cluster import SpectralClustering
import sklearn.datasets

X,y = sklearn.datasets.make_moons(200,noise=0.2)

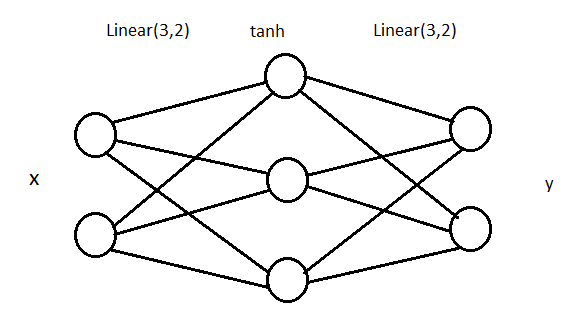
plt.scatter(X[:,0],X[:,1],s=40,c=y,cmap=plt.cm.Spectral)

可以看到生成了两类数据，分别用 0 和 1 来表示。我们接下来将要在这个样本数据上构造一个分类器，采用的是一个很简单的全连接网络，网络结构如下：

这个网络包含一个输入层，一个中间层，一个输出层。中间层包含 3 个神经元，使用的激活函数是 tanh。当然，中间层的神经元越多，分类效果一般越好，但这个 3 层的网络对于我们的样本数据已经足够用了。我们来算一下参数数量：上图中一共有 6+6 = 12 条线，就是 12 个权重，加上 3+ 2 = 5 个 bias，一共 17 个参数需要训练。

接下来将样本数据从 numpy 转成 tensor：

X = torch.from_numpy(X).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)

开始构建神经网络，其中损失函数用交叉熵损失函数，梯度优化器用Adam。 

import torch.nn as nn
import torch.nn.functional as F
 
class MyClassifier(nn.Module):
    def __init__(self):
        super(MyClassifier,self).__init__()
        self.fc1 = nn.Linear(2,3)
        self.fc2 = nn.Linear(3,2)
        
    def forward(self,x):
        x = self.fc1(x)
        x = F.tanh(x)
        x = self.fc2(x)
        return x
             
    def predict(self,x):
        pred = F.softmax(self.forward(x))
        ans = []
        for t in pred:
            if t[0]>t[1]:
                ans.append(0)
            else:
                ans.append(1)
        return torch.tensor(ans)

model = Net()
criterion = nn.CrossEntropyLoss()  #交叉熵损失函数
optimizer = torch.optim.Adam(model.parameters(), lr=0.01) #Adam梯度优化器

 训练：

epochs = 10000
losses = []
for i in range(epochs):
    y_pred = model.forward(X)
    loss = criterion(y_pred,y)
    losses.append(loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

查看训练误差： 

from sklearn.metrics import accuracy_score
print(accuracy_score(model.predict(X),y))

# Output
0.995

 下面的函数帮助我们在两个分类之间画一条分界线，便于将结果可视化。

def predict(x):
   x = torch.from_numpy(x).type(torch.FloatTensor)
   ans = model.predict(x)
   return ans.numpy()

def plot_decision_boundary(pred_func,X,y):
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max()+ .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max()+ .5
    h = 0.01
    xx,yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
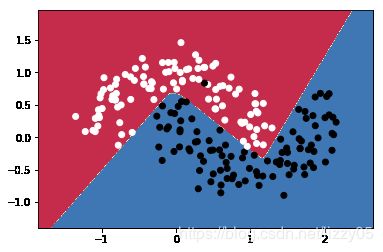
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.binary)

分类结果: 

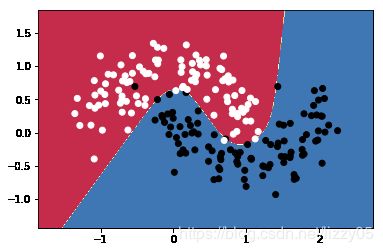
plot_decision_boundary(lambda x : predict(x) ,X.numpy(), y.numpy())

完整代码参见参考资料2，简单二分类器结果如下图所示 。

import sklearn.datasets
import torch
import numpy as np

np.random.seed(0)
X, y = sklearn.datasets.make_moons(200,noise=0.2)


import matplotlib.pyplot as plt

plt.scatter(X[:,0],X[:,1],s=40,c=y,cmap=plt.cm.binary)


X = torch.from_numpy(X).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)


import torch.nn as nn
import torch.nn.functional as F

#our class must extend nn.Module
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        #Our network consists of 3 layers. 1 input, 1 hidden and 1 output layer
        #This applies Linear transformation to input data. 
        self.fc1 = nn.Linear(2,3)
        
        #This applies linear transformation to produce output data
        self.fc2 = nn.Linear(3,2)
        
    #This must be implemented
    def forward(self,x):
        #Output of the first layer
        x = self.fc1(x)
        #Activation function is Relu. Feel free to experiment with this
        x = F.tanh(x)
        #This produces output
        x = self.fc2(x)
        return x
        
    #This function takes an input and predicts the class, (0 or 1)        
    def predict(self,x):
        #Apply softmax to output
        pred = F.softmax(self.forward(x))
        ans = []
        for t in pred:
            if t[0]>t[1]:
                ans.append(0)
            else:
                ans.append(1)
        return torch.tensor(ans)
        

#Initialize the model        
model = Net()
#Define loss criterion
criterion = nn.CrossEntropyLoss()
#Define the optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

#Number of epochs
epochs = 50000
#List to store losses
losses = []
for i in range(epochs):
    #Precit the output for Given input
    y_pred = model.forward(X)
    #Compute Cross entropy loss
    loss = criterion(y_pred,y)
    #Add loss to the list
    losses.append(loss.item())
    #Clear the previous gradients
    optimizer.zero_grad()
    #Compute gradients
    loss.backward()
    #Adjust weights
    optimizer.step()
    

from sklearn.metrics import accuracy_score
print(accuracy_score(model.predict(X),y))
    

def predict(x):
    x = torch.from_numpy(x).type(torch.FloatTensor)
    ans = model.predict(x)
    return ans.numpy()



    
# Helper function to plot a decision boundary.
# If you don't fully understand this function don't worry, it just generates the contour plot below.
def plot_decision_boundary(pred_func,X,y):
    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx,yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole gid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.binary)
    
    
plot_decision_boundary(lambda x : predict(x) ,X.numpy(), y.numpy())

# Output result:0.97

 

 

 

 

 

 

 

 

 

参考资料：

1. https://www.pytorchtutorial.com/pytorch-simple-classifier/

2. https://github.com/prudvinit/MyML/blob/master/lib/neural%20networks/pytorch%20moons.py

3. https://scikit-learn.org/stable/modules/classes.html#module-sklearn.cluster