神经网络算法

机器学习算法完整版见fenghaootong-github

神经网络原理

• 感知机学习算法
• 神经网络
  
  • 从感知机到神经网络
  • 多层前馈神经网络
  • bp算法

感知机学习算法

• 感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面，为求得超平面导入了基于误分类的损失函数，利用梯度下降法 对损失函数进行最优化（最优化）。
• 是神经网络和支持向量机的基础。

感知机定义

假设输入空间(特征向量)为 X⊆Rn X ⊆ R n ，输出空间为 Y=−1,+1 Y = − 1 , + 1 。输入 x∈X x ∈ X 表示实例的特征向量，对应于输入空间的点；输出 y∈Y y ∈ Y 表示示例的类别。由输入空间到输出空间的函数为

f(x⃗ )=sign(w⃗ ⋅x⃗ +b) f ( x → ) = s i g n ( w → ⋅ x → + b )

sign(x)={+1−1ifx≥0else s i g n ( x ) = { + 1 i f x ≥ 0 − 1 else

感知机学习策略

如果训练集是可分的，感知机的学习目的是求得一个能将训练集正实例点和负实例点完全分开的分离超平面。为了找到这样一个平面（或超平面），即确定感知机模型参数 w⃗  w → 和b，我们采用的是损失函数，同时并将损失函数极小化。

• 对于正确分类的样本点 (xi→,yi) ( x i → , y i ) , 有 (w⃗ ⋅xi→+b)yi>0 ( w → ⋅ x i → + b ) y i > 0
• 对于误分类的样本点 (xi→,yi) ( x i → , y i ) , 有 (w⃗ ⋅xi→+b)yi<0 ( w → ⋅ x i → + b ) y i < 0

误分类点到超平面的距离:

1||w⃗ ||2|(w⃗ ⋅xi→+b)| 1 | | w → | | 2 | ( w → ⋅ x i → + b ) |

||w⃗ ||2 | | w → | | 2 为 w⃗  w → 的 L2 L 2 范数

对于误分类点：

−(w⃗ ⋅xi→+b)yi>0 − ( w → ⋅ x i → + b ) y i > 0

−1||w⃗ ||2(w⃗ ⋅xi→+b)yi − 1 | | w → | | 2 ( w → ⋅ x i → + b ) y i

所有的点到超平面的距离:

−1||w⃗ ||2∑xi→∈M(w⃗ ⋅xi→+b)yi − 1 | | w → | | 2 ∑ x i → ∈ M ( w → ⋅ x i → + b ) y i

不考虑 1||w⃗ ||2 1 | | w → | | 2 ，就得到了感知机的损失函数：

L(w⃗ ,b)=−∑xi→∈M(w⃗ ⋅xi→+b)yi L ( w → , b ) = − ∑ x i → ∈ M ( w → ⋅ x i → + b ) y i

感知机学习算法

感知机学习转变成求解损失函数 L(w⃗ ,b) L ( w → , b ) 的最优化问题。最优化的方法是随机梯度下降法

minw⃗ ,bL(w⃗ ,b)=−minw⃗ ,b∑xi→∈M(w⃗ ⋅xi→+b)yi min w → , b L ( w → , b ) = − min w → , b ∑ x i → ∈ M ( w → ⋅ x i → + b ) y i

定义损失函数的梯度：

∇w⃗ L(w⃗ ,b)=−∑xi→∈Myixi→ ∇ w → L ( w → , b ) = − ∑ x i → ∈ M y i x i →

∇bL(w⃗ ,b)=−∑xi→∈Myi ∇ b L ( w → , b ) = − ∑ x i → ∈ M y i

随机选取一个误分类点，更新 w⃗ ,b w → , b 的值：

w⃗ :=w⃗ +ηyixi→ w → := w → + η y i x i →

b:=b+ηyi b := b + η y i

η∈(0,1] η ∈ ( 0 , 1 ]

神经网络

从感知机到神经网络

• 感知机可以看作神经网络的特例。感知机由两层神经元组成：输入层接收外界输入信号，输出层是M-P神经元。
• 感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元

多层前馈神经网络

• 感知机只拥有一层功能神经元，它只能处理线性可分的问题，要想解决非线性可分问题，可以使用多层功能神经元

• 神经网络的结构：

  • 每层神经元与下一层神经元全部相连
  • 同层神经元之间不存在连接
  • 跨层神经元之间也不存在连接

• 多层前馈神经网络有一下特点：

  • 掩藏层和输出层神经元都拥有激活函数
  • 输入层接收外界输入信号，不进行激活函数处理
  • 最终结果由输出层神经元给出

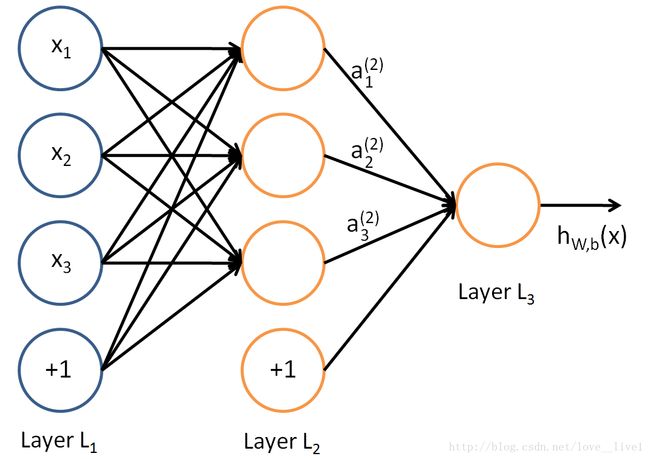
下图是一个简单的神经网络

激活函数

隐藏层和输出层都需要激活函数

我们选用sigmod函数作为激活函数：

z(l)i=∑j=1nW(l−1)ija(l−1)j+b(l−1)i z i ( l ) = ∑ j = 1 n W i j ( l − 1 ) a j ( l − 1 ) + b i ( l − 1 )

f(z(l)i)=11+e−z(l)i f ( z i ( l ) ) = 1 1 + e − z i ( l )

参数说明：

• a(l)i:表示第l层第i个单元的输出值 a i ( l ) : 表 示 第 l 层 第 i 个 单 元 的 输 出 值
• W(l)ij:表示第l层第j单元和第l+1层第i单元之间的权重 W i j ( l ) : 表 示 第 l 层 第 j 单 元 和 第 l + 1 层 第 i 单 元 之 间 的 权 重
• b(l)i:表示第l+1层第i单元的偏置项 b i ( l ) : 表 示 第 l + 1 层 第 i 单 元 的 偏 置 项
• z(l)i:表示第l层第i个单元输入加权和 z i ( l ) : 表 示 第 l 层 第 i 个 单 元 输 入 加 权 和

对于给定参数集合 W,b W , b ，我们的神经网络就可以按照函数 hW,b(x) h W , b ( x ) 来计算输出结果。上图神经网络的计算步骤如下：

a(2)1=f(W(1)11x1+W(1)12x2+W(1)13x3+b(1)1) a 1 ( 2 ) = f ( W 11 ( 1 ) x 1 + W 12 ( 1 ) x 2 + W 13 ( 1 ) x 3 + b 1 ( 1 ) )

a(2)2=f(W(1)21x1+W(1)22x2+W(1)23x3+b(1)1) a 2 ( 2 ) = f ( W 21 ( 1 ) x 1 + W 22 ( 1 ) x 2 + W 23 ( 1 ) x 3 + b 1 ( 1 ) )

a(2)3=f(W(1)31x1+W(1)32x2+W(1)33x3+b(1)2) a 3 ( 2 ) = f ( W 31 ( 1 ) x 1 + W 32 ( 1 ) x 2 + W 33 ( 1 ) x 3 + b 2 ( 1 ) )

hW,b(x)=a(3)1=f(W(1)11x1+W(1)12x2+W(1)13x3+b(1)1) h W , b ( x ) = a 1 ( 3 ) = f ( W 11 ( 1 ) x 1 + W 12 ( 1 ) x 2 + W 13 ( 1 ) x 3 + b 1 ( 1 ) )

上面的计算步骤叫做前向传播

反向传播算法

代价函数

C=12n∑i=1n||yi(x)−a(L)i(x)||2 C = 1 2 n ∑ i = 1 n | | y i ( x ) − a i ( L ) ( x ) | | 2

其中，x表示输入的样本，y表示实际的分类，a(L)表示预测的输出，L表示神经网络的最大层数。 其 中 ， x 表 示 输 入 的 样 本 ， y 表 示 实 际 的 分 类 ， a ( L ) 表 示 预 测 的 输 出 ， L 表 示 神 经 网 络 的 最 大 层 数 。

公式及其推导

首先，将第l层第i个神经元中产生的错误（即实际值与预测值之间的误差）定义为：

δ(l)i≡∂C∂z(l)i δ i ( l ) ≡ ∂ C ∂ z i ( l )

为了便于理解，下面都是一个样本

最后一层神经网络产生的错误：

δ(L)i=∇aC⊙f′(z(L)i) δ i ( L ) = ∇ a C ⊙ f ′ ( z i ( L ) )

⊙ ⊙ 用于矩阵或向量之间点对点的乘法运算

由后往前，计算每一层神经网络产生的错误：

δ(l)i=((w(l))Tδ(l+1)i)⊙f′(z(l)i) δ i ( l ) = ( ( w ( l ) ) T δ i ( l + 1 ) ) ⊙ f ′ ( z i ( l ) )

权重的梯度：

∂C∂w(l)ij=a(l)jδ(l+1)i ∂ C ∂ w i j ( l ) = a j ( l ) δ i ( l + 1 )

偏置的梯度：

∂C∂b(l)i=δ(l)i ∂ C ∂ b i ( l ) = δ i ( l )

使用梯度下降，训练参数：

w(l):=w(l)−ηm∑i=1nδ(l)i(a(l)i)T w ( l ) := w ( l ) − η m ∑ i = 1 n δ i ( l ) ( a i ( l ) ) T

b(l):=b(l)−ηm∑i=1nδ(l)i b ( l ) := b ( l ) − η m ∑ i = 1 n δ i ( l )

实例

神经网络应用实例