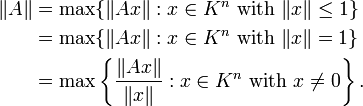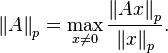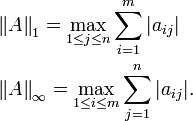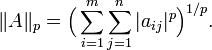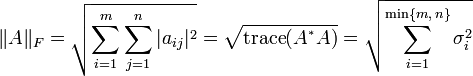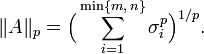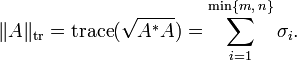矩阵范数（martix norm） --维基百科
矩阵范数（martix norm）是数学上向量范数对矩阵的一个自然推广。
目录[隐藏]
|
[编辑]矩阵范数的特性
以下 K 代表实数或复数域。现在考虑 
空间，亦即所有 m 行与 n 列的矩阵。
上的矩阵范数满足向量范数的所有特性，即若 
是矩阵 A 的范数，那么：
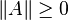，且等号成立当且仅当 A = 0 。
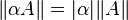，对于所有 α 属于 K 和所有矩阵 A 属于 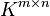成立。
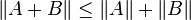，对于所有矩阵 A 和 B 属于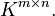 
此外，一些定义在n乘n矩阵上的矩阵范数（但并非所有这类的范数）满足一个或多个以下与“矩阵比纯粹一个向量有更多东西的事实”有关的条件：
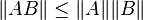
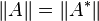，A * 是 A 的共轭转置（实矩阵就是普通转置）
一个满足第一个附加特性的矩阵范数被称为服从乘法范数（sub-multiplicative norm）。附上矩阵范数并包含所有 n×n 矩阵的集合，是巴拿赫代数的一个例子。
（在一些书上，术语“矩阵范数”只指服从乘法范数。）
[编辑]诱导范数
如果 Km 及 Kn 上向量范数已知（K 是实数或复数域），可在 
矩阵空间上按照下述原则定义相应的“诱导范数”或算子范数：
若 m = n 且在定义域和值域上使用相同的范数，则诱导的算子范数是服从乘矩阵范数。
举例说明, 与向量的 p-范数对应的算子范数是：
在 p = 1 且 
的情况下，其范数可以以下方式计算：
这些与矩阵的 Schatten p-范数不同, 也可以用 
来表示。
若满足 p = 2（欧几里德范数）且 m = n（方阵）此两特殊情况时，诱导的矩阵范数就是“谱范数”。矩阵 A 的谱范数是 A 最大的奇异值或半正定矩阵 A*A 的最大特征值的平方根：
其中 A* 代表 A 的共轭转置 。
任何矩阵范数满足此不等式
其中 ρ(A) 是 A 的谱半径。事实上，可以证明 ρ(A) 是 A 的所有诱导范数的下界。
此外，我们有
[编辑]矩阵元范数
这些向量范数将矩阵视为 向量，并使用类似的向量范数。
举例说明，使用向量的 p-范数，我们得到：
注：不要把矩阵元 p-范数与诱导 p-范数混淆。
[编辑]弗罗贝尼乌斯范数
对 p = 2，这称为弗罗贝尼乌斯范数（Frobenius norm）或希尔伯特-施密特范数（ Hilbert–Schmidt norm），不过后面这个术语通常只用于希尔伯特空间。这个范数可用不同的方式定义：
这里 A* 表示 A 的共轭转置，σi 是 A 的奇异值，并使用了迹函数。弗罗贝尼乌斯范数与 Kn 上欧几里得范数非常类似，来自所有矩阵的空间上一个内积。
弗罗贝尼乌斯范数是服从乘法的且在数值线性代数中非常有用。这个范数通常比诱导范数容易计算。
[编辑]极大范数
极大范数是 p=∞ 的元素范数，
这个范数不服从乘法。
[编辑]Schatten 范数
-
更多资料： Schatten范数
Schaten 范数出现于当 p-范数应用于一个矩阵的奇异值向量时。如果奇异值记做 σi， 则 Schatten p-范数定义为
这个范数与诱导、元素 p-范数使用了同样的记号，但它们是不同的。
所有 Schatten 范数服从乘法。它们也都是酉不变的，这就是说 ||A|| = ||UAV|| 对所有矩阵 A 与所有酉矩阵 U 和 V。
最常见的情形是 p = 1, 2, ∞。p = 2 得出弗罗贝尼乌斯范数，前面已经介绍过了。p = ∞ 得出谱范数，这是由向量 2-范数诱导的矩阵范数（见下）。最后， p = 1 得出迹范数，定义为
[编辑]一致范数
一个 上矩阵范数 
称为与 Kn 上向量范数 
以及 Km 上向量范数 一致，如果
对所有 
。根据定义，所有诱导范数是一致范数。
[编辑]范数的等价
对任何两个向量范数 ||·||α and ||·||β，我们有
对某个正数 r 与 s， 中所有矩阵 A 成立。换句话说，它们是等价的范数；它们在 上诱导了相同的拓扑。
此外，当 
，则对任何向量范数 ||·||，存在惟一一个正数 k 使得 k||A|| 是一个（服从乘法）矩阵范数。
一个矩阵范数 ||·||α 称为“极小的”，如果不存在其它矩阵范数 ||·||β 满足 ||·||β≤||·||α。
[编辑]范数等价的例子
对矩阵 
如下不等式成立[1][2]：
这里，||·||p 表示由向量 p-范数诱导的矩阵范数。
向量范数之间另一个有用的不等式是
[编辑]参考资料
- ^ Golub, Gene; Van Loan, Charles F., Matrix Computations. 3rd, Baltimore: The Johns Hopkins University Press. 1996: 56-57, ISBN 0-8018-5413-X
- ^ Horn, =Roger; Johnson, Charles, Matrix Analysis, Cambridge University Press. 1985, ISBN 0-521-38632-2
- Douglas W. Harder, Matrix Norms and Condition Numbers [1]
- James W. Demmel, Applied Numerical Linear Algebra, section 1.7, published by SIAM, 1997.
- Carl D. Meyer, Matrix Analysis and Applied Linear Algebra, published by SIAM, 2000. [2]