神经元模型和BP网络

神经元模型

+神经网络定义：具有适应性的简单单元组成的广泛并行互联网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。是机器学习与神经网络这两个学科的交叉部分。
+神经元模型：一种简单单元，M-P神经模型如下图：

+具体描述：神经元接收到来自n个其他的神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过“激活函数”处理以产生神经元的输出。
理想的激活函数为阶跃函数，‘1’对应于神经元的兴奋，‘0’对应于神经元的抑制，通常用Sigmoid函数作为激活函数。

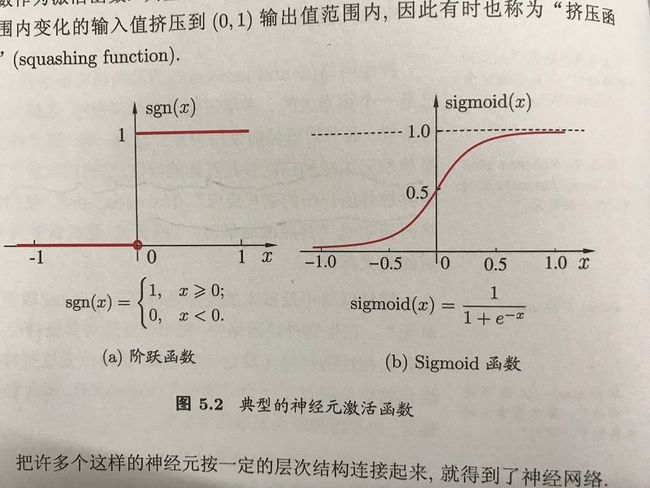
将许多这样的神经元按照一定的层次连接起来即为神经网络。

感知机与多层神经网络

+感知机：由两层神经元组成，输入层接受外界输入信号以后传递给输出层，输出层是M-P神经元。可以很容易的实现逻辑“或与非”，结构如下图：

一般情况下，权重 wi和阈值θ 可以通过学习得到。阈值\theta看做一个哑结点，对应权重\w_{i+1}，这样，权重和阈值的学习就可统一为权重的学习。
调整策略：

wi=wi+Δwi;Δwi=η(y−y^)xi,η∈(0,1)为学习率

若感知机对训练样例（x,y）预测正确，即 y^=y ，则感知机不发生变化，否则调整相应的参数。
+学习过程收敛
注感知机的与或非问题都是线性可分问题，可以用一个超平面将他们分开
两层感知机解决异或问题：

f函数为 sigmoid函数
y1=f(x1+x2−0.5);y2=f(−x1−x2+1.5);y=y1+y2

x1	x2	y1	y2	y
0	0	0	1	0
1	0	1	1	1
0	1	1	1	1
1	1	1	0	0

满足 x1⊕x2 问题

多层前馈网络：

前馈：网络拓扑结构不存在环或回路。
多层网络：一定包含隐层
神经网络的学习过程：根据训练数据来调整神经元之间的“连接权”以及每个功能的阈值。

误差逆传播算法（反向传播算法，BP算法）

给定训练集： D=(x1,y1),(x2,y2),...,(xm,ym)
定义如下变量：
d：输入神经元个数
l：输出实值向量个数
q：隐层神经元个数
θj ：输出层第j个神经元阈值
υh ：隐层第h个神经元
vih ：输入层第i个神经元与隐层第h个神经元之间的连接权
whj ：隐层第h个神经元与输出层第j个神经元与之间的连接权
图示：

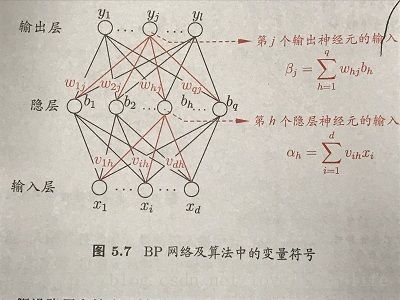
对训练集 (xk,yk) ，假定神经元的输出为 y^k=(y^k1,y^k2,...,y^kl) ，即： y^kj=f(βj−θj)⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅1
则网络在 （xk,yk） 上的均方误差为：

Ek=12∑j=1l(y^kj−ykj)2.⋅⋅⋅⋅⋅⋅⋅⋅⋅2

需要确定的参数：
+输入层到隐层的权值q*d个
+隐层到输出层的权值q*l个
+隐层的阈值q个
+输出层的阈值l个

更新公式：对任一参数v: v←v+Δv ·············3
BP算法求解策略：梯度下降法
（http://blog.csdn.net/loveitlovelife/article/details/78991472）

例：对隐层到输出层的权值调整： Δwhj=−η∂Ek∂whj ···········4

其中, η为学习率，Ek为误差；whj 为隐层第h个神经元到输出层第j个神经元的权值。
则：

∂Ek∂whj=∂Ek∂y^kj⋅∂y^kj∂βj∂βj∂whj⋅⋅⋅⋅⋅⋅⋅5

其中：
++由2式： ∂Ek∂y^kj=y^kj−ykj ；
++ ∂βj∂whj=bh ；其中 bh 为第h个隐层神经元输出；

++由于1式为sigmoid函数，且函数有如下性质f’(x)=f(x)(1-f(x))，

则：

∂y^kj∂βj=y^kj⋅（1−y^kj）

令： gj=−∂Ek∂y^kj⋅∂y^kj∂βj,⋅⋅⋅⋅⋅⋅⋅⋅6 得到：

Δwhj=ηgjbh⋅⋅⋅⋅⋅⋅⋅⋅⋅7

类似可得：

Δθj=−ηgj；Δvih=ηehxi;Δυh=−ηeh⋅⋅⋅⋅⋅⋅⋅8

推导过程：
http://blog.csdn.net/loveitlovelife/article/details/79075076
其中：

eh=−∂Ek∂bh⋅∂bh∂αh=−∑j=1l∂Ek∂βj⋅∂βj∂bh⋅f′(αh−υh)=∑j=1lwhjgjf′(αh−υh)=bh(1−bh)∑j=1lwhjgj⋅⋅⋅⋅⋅⋅9

η 太大容易震荡，太小收敛过慢，一般情况下 η=0.1

BP算法执行以下操作：
将输入示例提供给输入层神经元，然后逐层将信号前传，直到产生输出层结果；然后计算输出层误差，再将误差逆向传播至隐层神经元，最后根据隐层神经元的误差来对连接权和阈值进行调整，该迭代过程循环进行，直到达到停止条件为止。
算法伪代码：
过程：
1. 在（0，1）范围内随机初始化网络中所有连接权和阈值
2. repeat
3. for all (xk,yk)∈D do
4. 根据当前参数和1式计算当前样本的输出 y^k ；
5. 根据6式计算输出层神经元的梯度项 gj ；
6. 根据9式计算隐层神经元的梯度项 eh ；
7. 根据7、8式更新连接权 whj，vih 与阈值 θj，υh
8. end for
9. until 达到停止条件
输出：连接权与阈值确定的多层前馈神经网络

累积误差： E=1m∑mk=1Ek
若基于累积误差最小化的更新规则，则得到累积BP算法，与标准的BP算计法相比：
标准BP算法：更新针对单个样例，更新频繁；累积BP算法：读取整个训练集D后才对参数进行更新，更新频率低；累积误差下降到一定程度以后进一步下降非常缓慢，此时标准BP会获得比较好的解，训练集非常大时更明显。

未解决的问题：设置隐层神经元的个数，实际应用中常用“试错法”调整。

过拟合解决办法：BP神经网络场遭遇过拟合，因此有以下两种方法解决过拟合：1.“早停（early stopping）”：当训练集误差变小，测试集误差上升时，停止训练，返回连接权和阈值；2.“正则化（regularization）”：在误差目标函数中增加用于描述网络复杂度的部分，例如连接权与权值的平方和（L2范数），此时误差目标函数为： E=λ1m∑mk=1Ek+(1−λ)∑iw2i

全局最小和局部最小

+概念：
全局最小：所有点误差函数不小于该点函数值。
局部最小：邻域误差函数值不小于该点的函数值。

+寻优过程希望找到全局最小点
在BP算法寻找最小值过程中，若误差函数的梯度在当前点为0，则达到局部极小，未达到全局最小。

+达到全局最小的策略方法（启发式，无理论保障）：
1. 从多个不同的初始点开始搜索，可以获得接近全局最小的结果
2. 使用模拟退火技术，每一步以一定的概率接受比当前解更差的结果
3. 使用随机梯度下降
4. 遗传算法