贝叶斯分类器一

-贝叶斯决策论
-极大似然估计
-朴素贝叶斯分类器
-半朴素贝叶斯分类器
-贝叶斯网络

贝叶斯决策论

目标：基于概率和误判损失来选择最优的类别标记。

判定准则：
假设有N种可能的类别标记，即 υ={c1,c2,...,cN},λij υ = { c 1 , c 2 , . . . , c N } , λ i j 是将一个真实标记为 cj c j 的样本误分类为 ci c i 所产生的损失。基于后验概率 P(ci|x) P ( c i | x ) 可获得将样本x分类为 ci c i 所产生的期望损失，即在样本x上的“条件风险”:

R(ci|x)=∑j=1NλijP(cj|x). R ( c i | x ) = ∑ j = 1 N λ i j P ( c j | x ) .

我们的任务是寻找一个判定准则h: χ→υ χ → υ 以最小化总体风险：

R(h)=Ex[R(h(x)|x)] R ( h ) = E x [ R ( h ( x ) | x ) ]

.

贝叶斯准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险R(c|x)最小的类别标记，即

h∗(x)=argc∈υminR(c|x) h ∗ ( x ) = a r g c ∈ υ m i n R ( c | x )

, h∗ h ∗ 为贝叶斯最优分类器，贝叶斯风险 R(h∗),1−R(h∗) R ( h ∗ ) , 1 − R ( h ∗ ) 为分类器所能达到的最好性能。
误判损失：

λij={0,1,if i=jotherwise λ i j = { 0 , if i=j 1 , otherwise

条件风险：R(c|x) =1-P(c|x)
最小化分类错误率的贝叶斯最优分类器为：

h∗(x)=argc∈υmaxP(c|x), h ∗ ( x ) = a r g c ∈ υ m a x P ( c | x ) ,

即对每个样本x，选择能使后验概率P(c|x)最大的类别标记。

估计后验概率P(c|x)两种策略：
1生成式模型：先对联合概率分布P(x,c)建模，然后再由此获得P(c|x)，这样得到的是“生成式模型”。
2判别式模型：给定x，可通过直接建模P(c|x)来预测c,这样得到的是“判别式模型”（决策树、BP神经网络、支持向量机）

对于生成式模型： P(c|x)=P(x,c)P(x) P ( c | x ) = P ( x , c ) P ( x ) ，基于贝叶斯定理，则P(c|x)可写为：

P(c|x)=P(c)P(x|c)P(x) P ( c | x ) = P ( c ) P ( x | c ) P ( x )

其中，P(c)是类“先验概率”；P(x|c)是样本x相对于类标记c的类条件概率，P(x)证据因子，与类标记无关，因此我们只需估计 P(c)和P(x|c) P ( c ) 和 P ( x | c )

大数定律：数定律是指在随机试验中，每次出现的结果不同，但是大量重复试验出现的结果的平均值却几乎总是接近于某个确定的值。当训练集包含充足的独立同分布样本时，P(c)可以通过各类样本出现的频率来进行估计。http://wiki.mbalib.com/wiki/%E5%A4%A7%E6%95%B0%E5%AE%9A%E5%BE%8B

极大似然估计

假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。即：假定P(x|c)具有确定的形式，并且被参数向量 θc θ c 唯一确定，则可通过极大似然估计来估计参数 θc. θ c .
表示方法：令D_c表示训练集D中第c类样本组成的集合，假设这些样本独立同分布，则参数 θc θ c 对于数据集D_c的似然是：

P(Dc|θc)=∏x∈DcP(x|θc)(通常取对数⋅） P ( D c | θ c ) = ∏ x ∈ D c P ( x | θ c ) ( 通 常 取 对 数 · ）

此时参数 θc θ c 的极大似然估计 θ^c θ ^ c 为：

θ^c=argθcmaxLL(θc) θ ^ c = a r g θ c m a x L L ( θ c )

朴素贝叶斯分类器

采用“属性条件独立性假设”，假设每个属性独立的对分类结果发生影响，因此贝叶斯公式重写为：

P(c|x)=P(c)P(x|c)P(x)=P(c)P(x)∏i=1dP(xi|c) P ( c | x ) = P ( c ) P ( x | c ) P ( x ) = P ( c ) P ( x ) ∏ i = 1 d P ( x i | c )

,d为属性数目，x_i为x在第i个属性上的取值。
朴素贝叶斯分类器表达式：

hnb(x)=argc∈υmaxP(c)∏i=1dP(xi|c), h n b ( x ) = a r g c ∈ υ m a x P ( c ) ∏ i = 1 d P ( x i | c ) ,

先验概率估计： P(c)=|Dc|D P ( c ) = | D c | D ，D为训练集集合， Dc为C D c 为 C 类样本的集合。

条件概率估计:

P(xi|c)=|Dc,xi||Dc|. P ( x i | c ) = | D c , x i | | D c | .

拉普拉斯修正：（目的）：避免未出现的属性值被’抹去’，先验概率和条件概率分别修正为：
P(c)=|Dc|+1|D|+N P ( c ) = | D c | + 1 | D | + N ； P(xi|c)=|Dc,xi|+1|Dc|+Ni. P ( x i | c ) = | D c , x i | + 1 | D c | + N i .
其中： Dc D c 为第c类样本的集合，N为类别数， Dc,xi D c , x i 为第c类i属性的取值， Ni N i 为第i个属性的可能取值数。

半朴素贝叶斯分类器

基本思想：适当考虑一部分属性之间的相互依赖关系。“独依赖估计”是一种常用策略，即假设每个属性在类别之外最多仅依赖一个其他属性，即：

P(c|x)∝P(xi|c,pai), P ( c | x ) ∝ P ( x i | c , p a i ) ,

pa_i为x_i的父属性。
父属性的确定：假设所有属性都依赖于同一个属性，称为“超父”，通过交叉验证确定超父属性，形成SPODE方法，

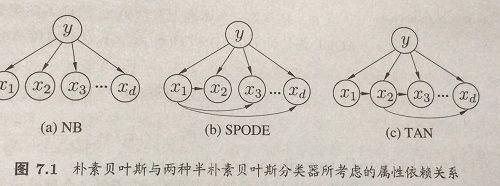
TAN方法：
1.计算任意两个属性之间的条件互信息：

I(xi,xj|y)=∑xi,xj;c∈υP(xi,xj|c)logP(xi,xj|c)P(xi|c)P(xj|c) I ( x i , x j | y ) = ∑ x i , x j ; c ∈ υ P ( x i , x j | c ) l o g P ( x i , x j | c ) P ( x i | c ) P ( x j | c )

2.以属性为结点构建完全图，任意两结点之间边的权重为 I(xi,xj|y); I ( x i , x j | y ) ;
3.构建此完全图的最大带权生成树，挑选根变量，将边置为有向；
4.加入类别结点y，增加从y到每个属性的有向边。

贝叶斯网

概念：借助有向无环图来刻画属性之间的依赖联系，并使用条件概率表来描述属性的联合概率分布。
构成：B= ⟨G,Θ⟩ ⟨ G , Θ ⟩ ，G是一个有向无环图，每个结点对应一个属性，若两个属性有直接依赖关系，则它们由一条边连接起来；参数 Θ Θ ，定量描述这种依赖关系，假设属性 xi x i 在G中的父节点集为 πi π i ，则 Θ Θ 包含了每个属性的条件概率表： θxi|πi=PB(xi|πi) θ x i | π i = P B ( x i | π i ) .

结构：有效表达了属性间的条件独立性。给定父节点，贝叶斯网假设每个属性与它的非后裔属性独立，于是B= ⟨G,Θ⟩ ⟨ G , Θ ⟩ 将属性 x1,x2,x3,...,xd x 1 , x 2 , x 3 , . . . , x d 的联合概率分布定义为：

PB(x1,x2,...,xd)=∏i=1dθxi|πi P B ( x 1 , x 2 , . . . , x d ) = ∏ i = 1 d θ x i | π i

其中 xi x i 为某结点； πi π i 为父节点集.

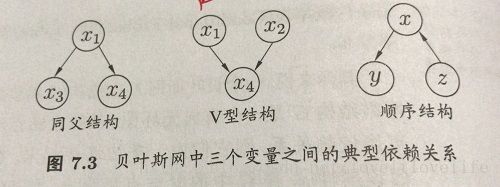
三个变量之间依赖关系详解：
1在同父结构中，给定父节点 x1 x 1 取值，则 x3与x4 x 3 与 x 4 条件独立。
2在顺序结构中，给定x取值，则y和z条件独立；
3在V型结构中，给定 x4 x 4 取值 ，x1,x2 ， x 1 , x 2 不独立； x4 x 4 未知则 x1,x2 x 1 , x 2 相互独立。

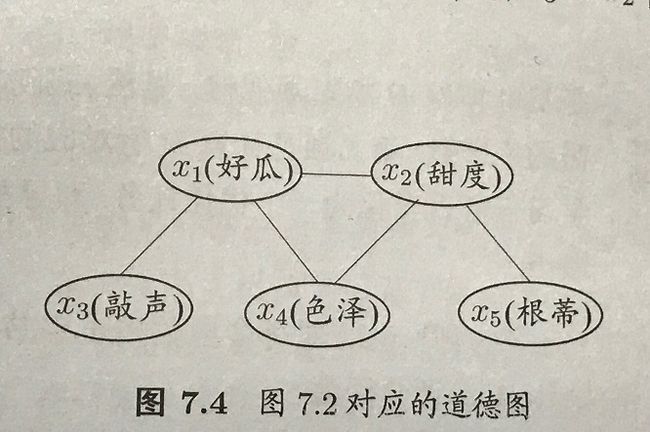
贝叶斯网络中条件独立性分析：
1.找出有向图中的所有V型结构，在V型结构中的两个父节点之间加上一条无向边；
2.将所有有向边改为无向边。

产生的无向图称为“道德图”，父节点相连的过程称为“道德化”。
判断标准：假定道德图中有变量x,y和变量集合z={z_i}，若变量x和y能在图上被z分开，即从道德图中将z去除以后，x和y分属两个连通分支，则称变量x和y被z有向分离， x⊥y|z x ⊥ y | z 成立

学习
1.网络结构已知：通过对训练样本计数，估计出每个节点的条件概率表即可。
2.网络结构未知：找出结构最恰当的贝叶斯网络。常用办法：定义评分函数，来估计贝叶斯网和训练数据的契合程度，然后基于这个评分函数来寻找最优结构的贝叶斯网。
3.学习目标：常用评分函数通常基于信息论准则，此类准则将学习问题看做一个数据压缩任务，学习的目标是找到一个能以最短的编码长度描述训练数据的模型，

“最小描述长度”准则：
给定训练集 D=x1,x2,x3,...,xm D = x 1 , x 2 , x 3 , . . . , x m ，贝叶斯网 B=⟨G,Θ⟩ B = ⟨ G , Θ ⟩ 在D上的评分函数可写为

s(B|D)=f(θ)|B|−LL(B|D)， s ( B | D ) = f ( θ ) | B | − L L ( B | D ) ，

第一项是计算编码贝叶斯网B所需的字节数；第二项1是计算B所对应的概率分布P_B对D描述得有多好，即寻找一个贝叶斯网B是评分函数s(B|D)最小。

AIC评分函数： AIC(B|D)=|B|−LL(B|D)，f(θ)=1 A I C ( B | D ) = | B | − L L ( B | D ) ， f ( θ ) = 1
BIC评分函数： BIC(B|D)=logm2|B|−LL(B|D) B I C ( B | D ) = l o g m 2 | B | − L L ( B | D )
若贝叶斯网 B=⟨G,Θ⟩ B = ⟨ G , Θ ⟩ 结构G固定，则评分函数第一项为固定值，此时最小化评分函数等价于对参数 Θ Θ 的极大似然估计。

推断
吉布斯采样法计算后验概率，算法步骤如下：
1. nq=0 n q = 0
2. q0=对Q随机赋初值 q 0 = 对 Q 随 机 赋 初 值
3. fort=1,2,...,Tdo f o r t = 1 , 2 , . . . , T d o
4. forQi∈Qdo f o r Q i ∈ Q d o
5. Z=E∪Q/{Qi}; Z = E ∪ Q / { Q i } ;
6. z=e∪qt−1/{qt−1i}; z = e ∪ q t − 1 / { q i t − 1 } ;
7. 根据B计算分布PB(Qi|Z=z); 根 据 B 计 算 分 布 P B ( Q i | Z = z ) ;
8. qti=根据PB(Qi|Z=z)采样所获得Qi取值; q i t = 根 据 P B ( Q i | Z = z ) 采 样 所 获 得 Q i 取 值 ;
9. qt=将qt−1中的qt−1i用qti替换 q t = 将 q t − 1 中 的 q i t − 1 用 q i t 替 换
10. endfor e n d f o r
11. ifqt=qthen i f q t = q t h e n
12. nq=nq+1 n q = n q + 1
13. endif e n d i f
14. end for
输出：P(Q=q|E=e)≃nqT 输 出 ： P ( Q = q | E = e ) ≃ n q T