Field D*路径规划算法
Field D*路径规划算法
- 1.栅格法路径规划存在的问题
- 2.Filed D*算法主要思想解析
- 3.Filed D*算法伪代码
- 4.算法优化
- 5.算法总结
- 参考文献
- 搜索算法其他文章
紧接着上一篇D* Lite路径规划算法,这一篇介绍D* Lite算法的改进版Field D*。
Filed D_star算法是D_star Lite算法的一种改进版本,该算法针对基于栅格的路径规划算法通常以栅格端点或中心点作为路径的节点,限制了路径方向变化只能为π/4的倍数,会导致机器人不必要的运动转向,影响执行效率。而Dave Ferguson提出的Filed D*算法,通过对栅格进行线性插值使路径点不局限于端点,规划方向的变化不再受限于π/4的倍数,生成较为平滑的路径。
1.栅格法路径规划存在的问题
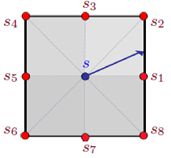
在规划2D网格时,通常从每个网格单元的中心进行规划,并且只允许转换到相邻网格单元的中心。这会将限制路径方向变化只能为π/4的倍数,从而导致路径为次优的,并且在实践中难以实现。如下图1所示,在实际的路径规划中,规划的路径只能走s点的8个方向(s1,s2,s3,s4,s5,s6,s7,s8),只能为π/4的倍数。
举个例子,机器人在如下图2没有障碍物的环境中,需要从起始点s运动到目标点g。显然,最优化的路径是起始点s到目标点g的直线。但是机器人的朝向角度为π/8,不是π/4的倍数,因而不能直接走s、g间的直线,只能按照 e 1 e_1 e1, e 2 e_2 e2走折线段。根据图中的计算可知,走 e 1 e_1 e1, e 2 e_2 e2的路线约多走8%的路程。
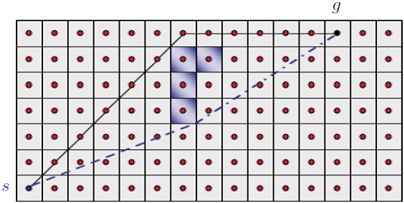
有一种方式可以缓解这种困难,例如在机器人起点s,寻找路径时,找到从s到p的直线路径无碰撞的最远点p,然后用这条直线路径替换原来的p路径(如图3)。但是,也不是总是有效的。在这里,基于网格的路径从s到g(顶部,黑色)不能平滑,因为有四个障碍单元(阴影)。最佳路径显示为虚线(蓝色)。
2.Filed D*算法主要思想解析
Filed D*算法的关键是在给定相邻节点路径代价的前提下,提出一种计算每个网格节点路径代价的新方法。在基于网格的路径规划中,一个节点的代价为(从节点到目标的路径代价):
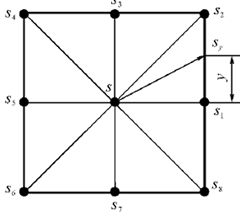
其中,nbrs(s)是s的所有相邻节点的集合;c(s, s’)是遍历s和s’之间的边的代价,g(s’)是节点s’的路径代价。而在此之前都是假设从节点s到相邻节点的唯一可能的移动只能是直线轨迹(只能是从一格移动到另一格)。而Filed D*考虑放宽这个假设,允许从节点s到其网格单元边界上的任何一点的直线轨迹(如下图4所示)。如果知道每一个点 s b s_b sb在边界的值,那么仅仅可以通过最小化 c ( s , s b ) + g ( s b ) c(s, s_b)+ g(s_b) c(s,sb)+g(sb)计算节点s的最优值, c ( s , s b ) c(s, s_b) c(s,sb)通过s和sb之间的距离乘以到达s所在单元的代价。但是,这样的点有无数个,因此不可能为每个点计算 g ( s b ) g(s_b) g(sb)。
但是,用线性插值法对每个边界点提供g(sb)的近似是可能的。首先将图4中的节点视为连续代价的样本点,由节点s开始的一条优化路径必须通过连接两个连续相邻的边缘,例如 s 1 s 2 ⃗ \vec{s_1s_2} s1s2。因此,设置通过这些边的路径的最小代价为s的路径代价,而这些边被认为是一次一条。为了通过 s 1 s 2 ⃗ \vec{s_1s_2} s1s2计算节点s的路径,需要使用节点 s 1 s_1 s1和 s 2 s_2 s2的路径代价以及图5(a)中所示中间网格的转移代价c和底部网格的转移代价b。
假设位于 s 1 s_1 s1和 s 2 s_2 s2之间边界上的任意点sy的路径代价是 g ( s 1 ) g(s_1) g(s1)和 g ( s 2 ) g(s_2) g(s2)的线性组合(如图6):
其中,其中y是 s 1 s_1 s1到 s y s_y sy的距离(假设单位单元格)。这个假设并不完美, s y s_y sy的路径代价可能不是 g ( s 1 ) g(s_1) g(s1)和 g ( s 2 ) g(s_2) g(s2)的线性组合,甚至也不是这些路径代价的函数。然而,这种线性近似在实际应用中效果良好,可以构造节点s路径代价的封闭形式解。根据这个近似,s在 s 1 s_1 s1、 s 2 s_2 s2、网格代价c和b下的路径代价可以计算为
这个公式可以通过上图7中的(a)图理解。公式中的第1项为s→ s x s_x sx的代价,第2项为 s x s_x sx→ s y s_y sy的代价,第3、4项为y处的代价。其中, x ∈ [ 0 , 1 ] x\in[0, 1] x∈[0,1], y ∈ [ 0 , 1 ] y\in[0, 1] y∈[0,1]。当x=y=1时,路径为底部的路径,但是代价却是中间网格的代价。
令 ( x ⃗ , y ⃗ ) (\vec{x},\vec{y}) (x,y)是一对解决上述最小化x和y的值。由于线性插值,这些值中至少有一个是0或1。直观地说,如果部分地穿过中心单元格要比绕边界而行花费更少,那么完全地穿过单元格的开销最小。因此,如果有任何代价最低的路径穿过中心网格,它将尽可能大,迫使x = 0或y = 1。如果没有路径穿过中心网格,然后y= 0。(详细证明见论文)
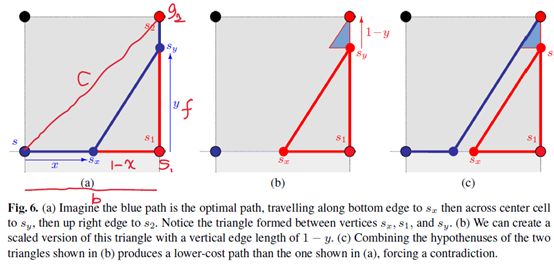
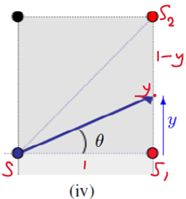
经过论证可知,路径要么沿着整个底部边缘 s 1 s_1 s1(图5(ii));或者将移动距离x底部边缘,然后直接沿着直线路径s2(图5(3));或将s到sy点直线路径右侧边缘(图5 (iv))。哪一条路代价低,取决于c,b的相对大小,路径 s 1 s_1 s1和 s 2 s_2 s2代价差异: f = g ( s 1 ) − g ( s 2 ) f = g(s_1)−g(s_2) f=g(s1)−g(s2)。具体来说,如果f < 0,那么从s到 s 1 s_1 s1的最优路径为 m i n ( c , b ) + g ( s 1 ) min(c, b)+g(s_1) min(c,b)+g(s1)(图5(ii))。如果f = b,那么使用底部边缘一部分路径的代价(图5(iii))将等于不使用底部边缘路径的成本(图5(iv))。可以解出后者的路径 y ⃗ \vec{y} y(等于 1 − x ⃗ 1-\vec{x} 1−x前路径),最小成本路径如下。首先,令k = f = b,s的路径代价为(图8示例说明)
上式对y求导,令为0,可得取最小值时的y值:
无论使用底边还是右边,最终得到的计算和路径代价都是相同的。所以重要的是哪条边代价更低。如果f < b,然后使用上面的右边缘,并如上计算路径的代价(当k = f);如果b < f,使用底部边缘,并用k = b和 y ⃗ = 1 − x ⃗ \vec{y}=1-\vec{x} y=1−x替代到上面的方程。对于任意两个相邻的 s a s_a sa和 s b s_b sb,计算s最小的路径代价算法如图9所示。
3.Filed D*算法伪代码
一旦对图中给定的节点进行了基于插值的路径代价计算,然后就可以将其插入许多路径规划算法中以生成平滑路径。图10给出了Field D_star公式,这是一种包含这些插值路径代价的增量重新规划算法。这个版本的Field D_star是基于D_star Lite算法的(不同之处用红色高亮显示)。与最初基于图形的D* Lite版本不同,{20 - 22}行将Field D_star裁剪为网格。同时,由于路径相交的不仅仅是节点, h ( s s t a r t , s ) h(s_{start}, s) h(sstart,s)必须足够小,当添加到从s发出的任何边的代价时,它仍然不大于从 s s t a r t s_{start} sstart到s的最小代价路径。
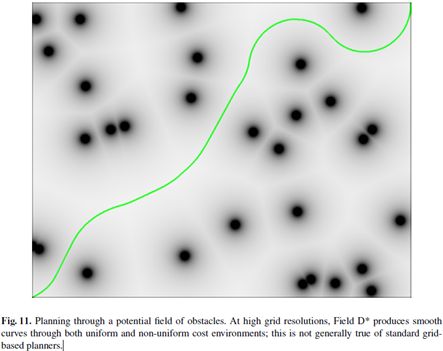
一旦计算出从初始状态到目标的路径的代价,就可以从初始位置开始扩展路径,并迭代计算要移动到下一个位置的单元边界点。由于插值技术,计算网格单元内任意一点的路径代价是可能的,而不仅仅是角落,这对于提取路径和在执行不完美的情况下返回轨道(通常对于真正的机器人是如此)都是有用的。Field D*应用的两个例子如下图11:
4.算法优化
为了减少计算量,通过在算法中降低被弹出状态的相邻点信息更新(第{09 - 14}行)时需要的计算量,只考虑那些被弹出状态的新值实际影响的状态以及这些状态是如何受到影响的。解决方案是引入状态函数bptr(s)、cknbr(s, s’)和ccknbr(s, s’),和对算法做出两处修改。最终的算法为:
5.算法总结
Filed D_star算法是基于D_star Lite算法进行改进的,与D_star Lite算法最大的不同在于路径搜索的过程中,搜索方向不再局限于只能为π/4的倍数,而可以是任意的方向,可以生成更为平滑的路径,同时尽可能是最优路径,而不是次优路径。但是,该算法同样存在一定的问题:由于 s y s_y sy的路径代价不一定符合 g ( s 1 ) g(s_1) g(s1)与 g ( s 2 ) g(s_2) g(s2)的线性组合,线性估计的误差随路径点代价的更新累积,导致插值点位置估计发生偏差,使其前后路径连线不一定共线。
参考文献
[1]马丽莎, 周文晖, 龚小谨, et al. 基于运动约束的泛化Field D~路径规划[J]. 浙江大学学报(工学版), 2012, 46(08): 1546-1552.
[2]Ferguson D, Stentz A. The Field D Algorithm for Improved Path Planning and Replanning in Uniform and Non-Uniform Cost Environments[C], 2005.
搜索算法其他文章
Dstar Lite路径规划算法
终身规划Astar算法(LPA*):Lifelong Planning A*
D*路径搜索算法原理解析及Python实现