深入理解AlexNet网络
AlexNet
论文:《ImageNet Classification with Deep Convolutional Neural Networks》
第一个典型的CNN是LeNet5网络结构,但是第一个引起大家注意的网络却是AlexNet,也就是文章《ImageNet Classification with Deep Convolutional Neural Networks》介绍的网络结构。这篇文章的网络是在2012年的ImageNet竞赛中取得冠军的一个模型整理后发表的文章。作者是多伦多大学的Alex Krizhevsky等人。Alex Krizhevsky其实是Hinton的学生,这个团队领导者是Hinton,那么Hinton是谁呢?这就要好好说说了,网上流行说 Hinton, LeCun和Bengio是神经网络领域三巨头,LeCun就是LeNet5作者(Yann LeCun),昨天的文章就提到了这个人。而今天的主角虽然不是Hinton,但却和他有关系,这篇的论文第一作者是Alex,所以网络结构称为AlexNet。这篇论文很有意思,因为我读完这篇论文之后,没有遇到比较难以理解的地方,遇到的都是之前学过的概念,比如Relu,dropout。之前学的时候只知道Relu是怎么一回事,今天才知道它真正的来源。这篇文章在2012年发表,文章中的模型参加的竞赛是ImageNet LSVRC-2010,该ImageNet数据集有1.2 million幅高分辨率图像,总共有1000个类别。测试集分为top-1和top-5,并且分别拿到了37.5%和17%的error rates。这样的结果在当时已经超过了之前的工艺水平。AlexNet网络结构在整体上类似于LeNet,都是先卷积然后在全连接。但在细节上有很大不同。AlexNet更为复杂。AlexNet有60 million个参数和65000个 神经元,五层卷积,三层全连接网络,最终的输出层是1000通道的softmax。AlexNet利用了两块GPU进行计算,大大提高了运算效率,并且在ILSVRC-2012竞赛中获得了top-5测试的15.3%error rate, 获得第二名的方法error rate 是 26.2%,可以说差距是非常的大了,足以说明这个网络在当时给学术界和工业界带来的冲击之大。
一些背景
在计算机视觉领域object detection & recognition 通常用机器学习的方法来解决。为了提高识别的效果,我们可以通过收集更多的可训练的数据来让模型的泛化性能提高。目前,在以一万为单位的数量级层面的数据(称为简单的识别任务)已经获得了非常好的性能,例如:MNIST 手写数字识别任务,最好的性能已经达到了<0.3%的误差。但是现实中的物体存在相当多的变化属性,所以学习识别它们需要更多的数据。事实上,小的图像训练数据有很多的缺点,无论以我们的直觉想还是理论证明都是有依据的,理论上论文《Why is real-world visual object recognition hard?》给出了研究方法。随着互联网技术的发展,以及智能手机的普及图像数据获取可以说越来越容易。所以就有组织去收集这些现实中事物的图像并进行标记和分割。例如:LabelMe(Labelme: a database and web-based tool for image annotation. ),包含了成百上千的全分割图像。 ImageNet(ImageNet: A Large-Scale Hierarchical Image Database. I),包含15 billion 标记的高分辨率图像,包含超过了22000种现实中的事物。
文章中说该模型有5层卷积,去掉任意一层都会使结果不好,所以这个网络的深度似乎是很重要的,这样的话难免引起我们的思考,记得不知道哪位大神在一篇论文中证明了,神经网络可以模拟任意多项式,只要神经元数量足够多,并且和深度关系不大。但这里的实验却表示深度会对网络的性能有影响。
文章中还提到了,他们用5-6天训练了这个模型,并且限制了网络的大小,因为现有的硬件智能允许那么大的内存,用更好的设备还可以获得更好的效果。
网络结构
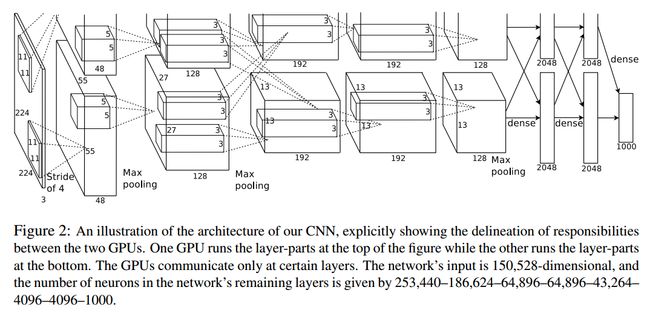
AlexNet 的网络结构是这样的,为啥我感觉这样表示的网络很丑呀,哈哈。
感觉这个网络很复杂呀,需要怎么理解好呢?首先这幅图分为上下两个部分的网络,论文中提到这两部分网络是分别对应两个GPU,只有到了特定的网络层后才需要两块GPU进行交互,这种设置完全是利用两块GPU来提高运算的效率,其实在网络结构上差异不是很大。为了更方便的理解,我们假设现在只有一块GPU或者我们用CPU进行运算,我们从这个稍微简化点的方向区分析这个网络结构。网络总共的层数为8层,5层卷积,3层全连接层。
第一层:卷积层1,输入为 224 × 224 × 3 224 \times 224 \times 3 224×224×3的图像,卷积核的数量为96,论文中两片GPU分别计算48个核; 卷积核的大小为 11 × 11 × 3 11 \times 11 \times 3 11×11×3; stride = 4, stride表示的是步长, pad = 0, 表示不扩充边缘;
卷积后的图形大小是怎样的呢?
wide = (224 + 2 * padding - kernel_size) / stride + 1 = 54
height = (224 + 2 * padding - kernel_size) / stride + 1 = 54
dimention = 96
然后进行 (Local Response Normalized), 后面跟着池化pool_size = (3, 3), stride = 2, pad = 0 最终获得第一层卷积的feature map
最终第一层卷积的输出为
第二层:卷积层2, 输入为上一层卷积的feature map, 卷积的个数为256个,论文中的两个GPU分别有128个卷积核。卷积核的大小为: 5 × 5 × 48 5 \times 5 \times 48 5×5×48; pad = 2, stride = 1; 然后做 LRN, 最后 max_pooling, pool_size = (3, 3), stride = 2;
第三层:卷积3, 输入为第二层的输出,卷积核个数为384, kernel_size = ( 3 × 3 × 256 3 \times 3 \times 256 3×3×256), padding = 1, 第三层没有做LRN和Pool
第四层:卷积4, 输入为第三层的输出,卷积核个数为384, kernel_size = ( 3 × 3 3 \times 3 3×3), padding = 1, 和第三层一样,没有LRN和Pool
第五层:卷积5, 输入为第四层的输出,卷积核个数为256, kernel_size = ( 3 × 3 3 \times 3 3×3), padding = 1。然后直接进行max_pooling, pool_size = (3, 3), stride = 2;
第6,7,8层是全连接层,每一层的神经元的个数为4096,最终输出softmax为1000,因为上面介绍过,ImageNet这个比赛的分类个数为1000。全连接层中使用了RELU和Dropout。
上面的结构是假设在一块GPU上面的,和论文的两块GPU有差别,但是为了方便理解,还是采用越简单的结构越好。
ReLU Nonlinearity(Rectified Linear Unit)
标准的L-P神经元的输出一般使用tanh 或 sigmoid作为激活函数, t a n h ( x ) = s i n h x c o s h x = e x − e − x e x + e − x tanh(x) = \frac{sinhx}{coshx} = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=coshxsinhx=ex+e−xex−e−x, sigmoid: f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1。但是这些饱和的非线性函数在计算梯度的时候都要比非饱和的现行函数 f ( x ) = m a x ( 0 , x ) f(x) = max(0, x) f(x)=max(0,x)慢很多,在这里称为 Rectified Linear Units(ReLUs)。在深度学习中使用ReLUs要比等价的tanh快很多。

上图是使用ReLUs和tanh作为激活函数的典型四层网络的在数据集CIFAR-10s实验中,error rate收敛到0.25时的收敛曲线,可以很明显的看到收敛速度的差距。虚线为tanh,实线是ReLUs。
Local Response Normalization(局部响应归一化)
在神经网络中,我们用激活函数将神经元的输出做一个非线性映射,但是tanh和sigmoid这些传统的激活函数的值域都是有范围的,但是ReLU激活函数得到的值域没有一个区间,所以要对ReLU得到的结果进行归一化。也就是Local Response Normalization。局部响应归一化的方法如下面的公式:
b ( x , y ) i = a ( x , y ) i ( k + α ∑ j = m a x ( 0 , i − n / 2 ) m i n ( N − 1 , i + n / 2 ) ( a ( x , y ) j ) 2 ) β b^{i}_{(x, y)} = \frac{a^{i}_{(x, y)}}{(k + \alpha \sum\limits_{j = max(0, i - n / 2)}^{min(N-1, i+n / 2)}(a^j_{(x, y)})^2)^{\beta}} b(x,y)i=(k+αj=max(0,i−n/2)∑min(N−1,i+n/2)(a(x,y)j)2)βa(x,y)i
这个公式什么意思呢? a ( x , y ) i a^i_{(x, y)} a(x,y)i代表的是ReLU在第i个kernel的(x, y)位置的输出,n表示的是 a ( x , y ) i a^i_{(x, y)} a(x,y)id的邻居个数,N表示该kernel的总数量。 b ( x , y ) i b^i_{(x,y)} b(x,y)i表示的是LRN的结果。ReLU输出的结果和它周围一定范围的邻居做一个局部的归一化,怎么理解呢?我觉得这里有点类似域我们的最大最小归一化,假设有一个向量X = [x_1, x_2, …x_n]
那么将所有的数归一化到0-1之间的归一化规则是: x i = x i x m a x − x m i n x_i = \frac{x_i}{x_{max} - x_{min}} xi=xmax−xminxi。
上面那个公式有着类似的功能,只不过稍微负载一些,首先运算略微复杂,其次还有一些其他的参数 α , β , k \alpha, \beta, k α,β,k。
我们看上图,每一个矩形表示的一个卷积核生成的feature map。所有的pixel已经经过了ReLU激活函数,现在我们都要对具体的pixel进行局部的归一化。假设绿色箭头指向的是第i个个kernel对应的map,其余的四个蓝色箭头是它周围的邻居kernel层对应的map,假设矩形中间的绿色的pixel的位置为(x, y),那么我需要提取出来进行局部归一化的数据就是周围邻居kernel对应的map的(x, y)位置的pixel的值。也就是上面式子中的 a ( x , y ) j a^j_{(x, y)} a(x,y)j。然后把这些邻居pixel的值平方再加和。乘以一个系数 α \alpha α再加上一个常数k,然后 β \beta β次幂,就是分母,分子就是第i个kernel对应的map的(x, y)位置的pixel值。这样理解之后我感觉就不是那么复杂了。
关键是参数 α , β , k \alpha, \beta, k α,β,k如何确定,论文中说在验证集中确定,最终确定的结果为:
k = 2 , n = 5 , α = 1 0 − 4 , β = 0.75 k=2, n=5, \alpha=10^{-4}, \beta = 0.75 k=2,n=5,α=10−4,β=0.75
Overlapping Pooling(覆盖的池化操作)
一般的池化层因为没有重叠,所以pool_size 和 stride一般是相等的,例如 8 × 8 8\times 8 8×8的一个图像,如果池化层的尺寸是 2 × 2 2 \times 2 2×2,那么经过池化后的操作得到的图像是 4 × 4 4 \times 4 4×4大小,这种设置叫做不覆盖的池化操作,如果 stride < pool_size, 那么就会产生覆盖的池化操作,这种有点类似于convolutional化的操作,这样可以得到更准确的结果。在top-1,和top-5中使用覆盖的池化操作分别将error rate降低了0.4%和0.3%。论文中说,在训练模型过程中,覆盖的池化层更不容易过拟合。
Overall Architecture
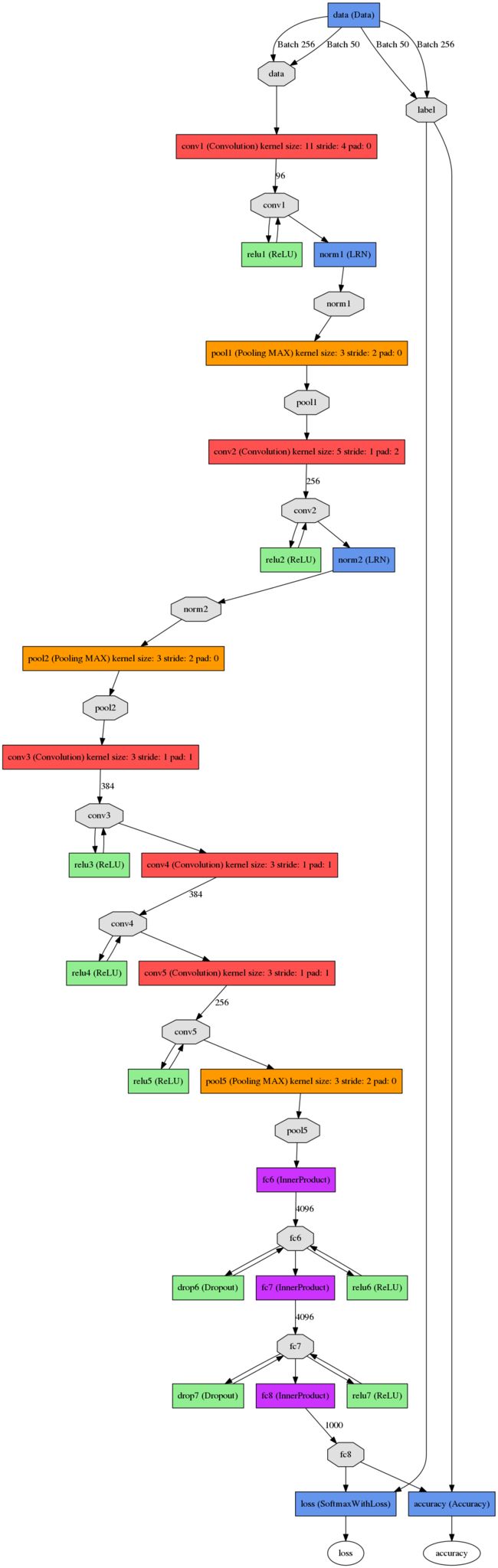
用caffe 自带的绘图工具(caffe/python/draw_net.py) 和caffe/models/bvlc_alexnet/目录下面的train_val.prototxt绘制的网络结构图如下图
防止过拟合的方法
神经网络的一个比较严重的问题就是过拟合问题,论文中采用的数据扩充和Dropout的方法处理过拟合问题。
Data Augmentation(数据扩张,就是对原始数据做一些变化)
数据扩充是防止过拟合的最简单的方法,只需要对原始的数据进行合适的变换,就会得到更多有差异的数据集,防止过拟合。
Dropout
Dropout背后有很多有意思的东西,但是在这里我们不需要了解太深,只需要知道Dropout是在全连接层中去掉了一些神经节点,达到防止过拟合的目的,我们可以看上面的图在第六层和第七层都设置了Dropout。关于DropOut的理解,推荐一篇文章
Reference
- AlexNet 原始论文
- caffe AlexNet
- dropout 理解
- 机器学习进阶笔记之三|深入理解Alexnet