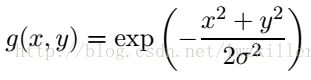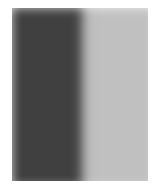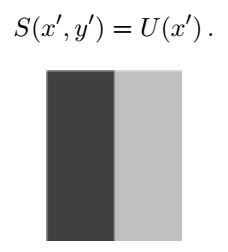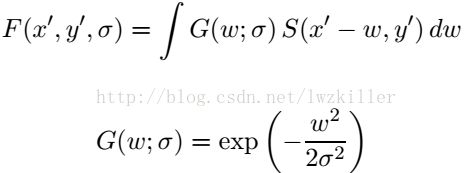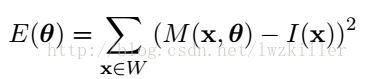亚像素级点定位及边缘定位算法
在这篇博客里,主要讲解两点:点定位(Point localization)以及边缘定位(Edge localization),均是亚像素级定位精度。当然还有其他定位方法,这里仅针对亮点和边缘两种情形分别进行精确定位。
1. 为何需要进行亚像素定位?
>数字图像通常是被离散化成像素形式;
>每个像素对应一个整数坐标位置;
>整数坐标位置对于很多应用然而并不精确,比如跟踪、相机标定、图像配准、图像拼接以及三维重构;
>为达到有些应用的精确性,需要精确到浮点坐标位置;
所以会涉及到亚像素定位问题。亚像素定位就是计算特征所在图像中的真实位置,而真实位置有时候并不在像素所在整数坐标位置上,而是在像素的内部。
2. 基本思想
>设计一个特征模型以便进行定位,通常使用数学模型来描述图像的特征,数学模型也不一定就完全能表达图像的特征,至少能接近,否则设计的模型欠妥;
>使用常用算法进行定位,初定位精度一般达到整数坐标位置即可,通常初定位的精度要保证至少在精确位置附近,否则偏离较远,算法计算可能也会实效;
>反复迭代使用匹配模型进行精确定位,检测图像特征位置,使特征位置精度达到亚像素级别,迭代的目的通常是优化模型参数;
注意,大多数亚像素定位算法需要对特征所在的位置有一个良好的估计,否则会将图像上的噪声位置误认为期望的特征位置。
3. 点定位
首先,点在图像里是如何呈现的?如下图所示:
>一个“点”通常会占用多个像素;
>一个“点”通常也不具有强边缘性质,其边缘通常是光滑的、模糊的;
那么我们当然不能以一个像素区域作为“点”的位置,应该以一个坐标点来标记这个“点”的位置,通常计算点区域的中心位置 或者 点区域的最亮位置所对应的坐标, 那么如何去计算该点的位置呢?
结合上图所示,点的灰度分布特征是不是跟二维高斯模型很相似?中心处最亮,离中心距离越远会随之变暗。所以这里的图像特征,我们用高斯模型进行描述。
利用高斯模型,我们可以构建点的最终模型函数M,如下:
说明下,这个模型比单独的高斯模型更适合表达图像特征,如果仅仅用高斯模型,那么离中心越远,图像亮度越小,但图像的亮度的最小程度也就是四周的暗区域,这些暗区域的灰度强度值并不为0,而是A。
上述表达式中的各个参数解释如下:
>M:代表对应像素位置上的强烈程度
>(x,y):图像中某个像素位置
>A:背景的强烈程度,比如上面的黑色区域
>B:亮区域中的强烈程度的峰值
>(u,v):亮区域中的峰值所在的位置
>sigma:高斯模型方差
上面左边表达式可以简化为:![]() ,其中
,其中![]() 表示图像的像素位置;
表示图像的像素位置;![]() 是点的模型参数,当模型参数已知,那么图像特征已被定位,也就是高斯模型的中心位置(u,v),该坐标位置是浮点型的,也即是亚像素别级的。
是点的模型参数,当模型参数已知,那么图像特征已被定位,也就是高斯模型的中心位置(u,v),该坐标位置是浮点型的,也即是亚像素别级的。
针对图像中存在"点"情形,如果模型![]() ,即对应像素位置的强度与模型函数M估计出来的强度相同,那么我们认为用该模型匹配点区域的像素值是完美的,该模型是适合描述该区域的特征。事实上,在点区域里,保证不了左右两等式相等,我们只求左右两等式尽量逼近,那么如何获取一个良好的匹配模型呢,也即如何求解出模型的最佳参数呢?基本都是通过残差进行分析,如:
,即对应像素位置的强度与模型函数M估计出来的强度相同,那么我们认为用该模型匹配点区域的像素值是完美的,该模型是适合描述该区域的特征。事实上,在点区域里,保证不了左右两等式相等,我们只求左右两等式尽量逼近,那么如何获取一个良好的匹配模型呢,也即如何求解出模型的最佳参数呢?基本都是通过残差进行分析,如:
 ,其中W相当于一个窗口或者是一个模板,所以W窗口移动到点附近哪个位置是最合适的?在进行残差计算前,首先使用一个简单算法粗定位一个位置,将窗口中心移动至该位置上,再进行残差计算。我们的目的是最小化误差
,其中W相当于一个窗口或者是一个模板,所以W窗口移动到点附近哪个位置是最合适的?在进行残差计算前,首先使用一个简单算法粗定位一个位置,将窗口中心移动至该位置上,再进行残差计算。我们的目的是最小化误差![]() ,即可获取亚像素位置坐标(u,v)。 亚像素定位方法可以直接对误差函数的每一个参数进行偏导求取,也可以使用梯度下降法进行求解,最终得到模型的相关参数(这里极有可能得到的解是局部最优解)。当然求解的方法很多,最好使用的方法能解出全局最优解,这样解的模型才是最优的。
,即可获取亚像素位置坐标(u,v)。 亚像素定位方法可以直接对误差函数的每一个参数进行偏导求取,也可以使用梯度下降法进行求解,最终得到模型的相关参数(这里极有可能得到的解是局部最优解)。当然求解的方法很多,最好使用的方法能解出全局最优解,这样解的模型才是最优的。
4. 边缘定位
边缘定位算法跟点定位算法相似。 下面是一幅带有边缘的图像:
这里着重讲解下边缘模型的推导:
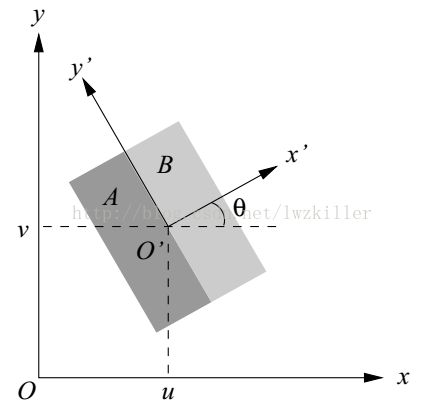
对于单位跃阶边缘,我们可以定义如下:
因此,对于一个理想的二维跃阶边缘,以![]() 为坐标系,那么沿着
为坐标系,那么沿着![]() 轴方向有:
轴方向有:
这里我们可以假设一个模型来对实际边缘进行模拟,实际边缘其实是模糊的,没有跃阶现象,那么我们可以认为实际边缘是由一个二维的跃阶边缘与一个一维的高斯函数进行卷积形成的:
其中![]() 在图像坐标系中的位置为(u,v).
在图像坐标系中的位置为(u,v).
所以,需要定位的亚像素位置应该是理想中的二维跃阶边缘位置,在真实边缘图像中,该位置应该是从暗到亮转变过程中,导数发生最大变化所对应的位置。
此时我们结合上面坐标系图示,可以得到边缘点在局部坐标系和图像坐标系位置转换关系
我们最终建立的边缘模型可以表示为:
求解参数,仍是使用误差函数分析,使误差函数最小化,此处的W是一窗口或者模板
可以使用梯度下降法优化残差函数,求取![]() ,最终获得(u,v),也即是定位得到的边缘亚像素位置,边缘方向是垂直于theta角的。
,最终获得(u,v),也即是定位得到的边缘亚像素位置,边缘方向是垂直于theta角的。
当然,亚像素定位算法很多,视图像的具体特征而定,欢迎讨论留言。