prim最小生成树算法原理

prim 最小生成树算法原理 主要需要了解算法的原理、算法复杂度、优缺点 、刻画和度量指标 评价等 可以查阅相关的文献，这部分内容主要整合了两篇博客的内容

分别是：http://blog.csdn.net/tham_/article/details/46048907 这一篇重点在于算法的复杂度

http://blog.csdn.net/hnust_xiehonghao/article/details/38013125 这一篇主要是帮助理解prim的算法原理

这篇文章是对《算法导论》上Prim算法求无向连通图最小生成树的一个总结，其中有关于我的一点点小看法。

　　最小生成树的具体问题可以用下面的语言阐述：
　　　　输入：一个无向带权图G=(V,E)，对于每一条边(u, v)属于E，都有一个权值w。

　　　　输出：这个图的最小生成树，即一棵连接所有顶点的树，且这棵树中的边的权值的和最小。

　　举例如下，求下图的最小生成树：

　　这个问题是求解一个最优解的过程。那么怎样才算最优呢？

　　首先我们考虑最优子结构：如果一个问题的最优解中包含了子问题的最优解，则该问题具有最优子结构。

　　最小生成树是满足最优子结构的，下面会给出证明：

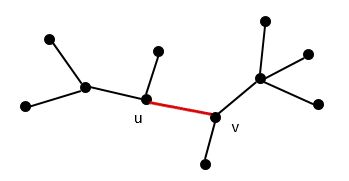
　　最优子结构描述：假设我们已经得到了一个图的最小生成树(MST) T，(u, v)是这棵树中的任意一条边。如图所示：

　　现在我们把这条边移除，就得到了两科子树T₁和T_{2，如图：}

 

　　T₁是图G₁=(V₁, E₁)的最小生成树，G₁是由T₁的顶点导出的图G的子图，E₁={(x, y)∈E, x, y ∈V₁}

　　同理可得T₂是图G₂=(V₂, E₂)的最小生成树，G₂是由T₂的顶点导出的图G的子图，E₂={(x, y)∈E, x, y ∈V₂}

　　现在我们来证明上述结论：使用剪贴法。w(T)表示T树的权值和。

　　　　首先权值关系满足：w(T) = w(u, v)+w(T₁)+w(T₂)

　　　　假设存在一棵树T₁'比T₁更适合图G1，那么就存在T'={(u,v)}UT₁'UT₂'，那么T'就会比T更适合图G，这与T是最优解相矛盾。得证。

　　因此最小生成树具有最优子结构，那么它是否还具有重叠子问题性质呢？我们可以发现，不管删除那条边，上述的最优子结构性质都满足，都可以同样求解，因此是满足重叠子问题性质的。

　　考虑到这，我们可能会想：那就说明最小生成树可以用动态规划来做咯？对，可以，但是它的代价是很高的。

　　我们还能发现，它还有个更强大的性质：贪心选择性质。因而可用贪心算法完成。

　　贪心算法特点：一个局部最优解也是全局最优解。

　　最小生成树的贪心选择性质：令T为图G的最小生成树，另A⊆V，假设边(u, v)∈E是连接着A到A的补集（也就是V-A)的最小权值边，那么(u, v)属于最小生成树。

　　证明：假设(u, v)∉T， 使用剪贴法。现在对下图进行分析，图中A的点用空心点表示，V-A的点用实心点表示：

　　在T树中，考虑从u到v的一条简单路径（注意现在(u, v)不在T中），根据树的性质，它是唯一的。

　   现在把(u, v)和这条路上中的第一条连接A和V-A的边交换，即画红杠的那条边，边(u, v)是连接A和V-A的权值最小边，那我们就得到了一棵更小的树，这就与T是最小　　生成树矛盾。得证。

　　现在呢，我们来看看Prim的思想：Prim算法的特点是集合E中的边总是形成单棵树。树从任意根顶点s开始，并逐渐形成，直至该树覆盖了V中所有顶点。每次添加到树中的边都是使树的权值尽可能小的边。因而上述策略是“贪心”的。

　　算法的输入是无向连通图G=(V, E)和待生成的最小生成树的根r。在算法的执行过程中，不在树中的所有顶点都放在一个基于key域的最小优先级队列Q中。对每个顶点v来说，key[v]是所有将v与树中某一顶点相连的边中的最小权值；按规定如果不存在这样的边，则key[v]=∞。

　　实现Prim算法的伪代码如下所示：

　　MST-PRIM(G, w, r)

　　　　for each u∈V

　　　　　　do key[u] ← ∞

　　　　　　　  parent[u]← NIL

　　　　key[r] ← 0

　　　　Q ← V

　　　　while Q ≠∅

　　　　　　do u ← EXTRACT-MIN(Q)

　　　　　　　　for each v∈Adj[u]

　　　　　　　　　　do if v∈Q and w(u, v) < key[v]

　　　　　　　　　　　　then parent[v] ← u

　　　　　　　　　　　　　　  key[v] ← w(u, v)

　　其工作流程为：

　　　　（1）首先进行初始化操作，将所有顶点入优先队列，队列的优先级为权值越小优先级越高

　　　　（2）取队列顶端的点u，找到所有与它相邻且不在树中的顶点v，如果w(u, v) < key[v]，说明这条边比之前的更优，加入到树中，即更改父节点和key值。这中间还　　　　隐含着更新Q的操作（降key值）

　　　　（3）重复2操作，直至队列空为止。

　　　　（4）最后我们就得到了两个数组，key[v]表示树中连接v顶点的最小权值边的权值，parent[v]表示v的父结点。

　　现在呢，我们发现一个问题，这里要用到优先队列来实现这个算法，而且每次搜索邻接表都要进行队列更新的操作。

　　不管用什么方法，总共用时为O(V*T(EXTRACTION)+E*T(DECREASE))

　　　　（1）如果用数组来实现，总时间复杂度为O(V²)

　　　　（2）如果用二叉堆来实现，总时间复杂度为O(ElogV)

　　　　（3）如果使用斐波那契堆，总时间复杂度为O(E+VlogV)

　　上面的三种方法，越往下时间复杂度越好，但是实现难度越高，而且每次对最小优先队列的更新是非常麻烦的，那么，有没有一种方法，可以不更新优先队列也达到同样的　　效果呢？

　　答案是：有。

　　其实只需要简单的操作就可以达到。首次只将根结点入队列。第一次循环，取出队列顶结点，将其退队列，之后找到队列顶的结点的所有相邻顶点，若有更新，则更新它们的key值后，再将它们压入队列。重复操作直至队列空为止。因为对树的更新是局部的，所以只需将相邻顶点key值更新即可。push操作的复杂度为O(logV)，而且省去了之前将所有顶点入队列的时间，因而总复杂度为O(ElogV)。

　　具体实现代码，邻接矩阵优先队列可以用STL实现：

 #include
 #include
 #include
 #include
 using namespace std;

 #define maxn 110  //最大顶点个数
 int n, m;       //顶点数，边数

 struct arcnode  //边结点
 {
     int vertex;     //与表头结点相邻的顶点编号
     int weight;     //连接两顶点的边的权值
     arcnode * next; //指向下一相邻接点
     arcnode() {}
     arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}
 };

 struct vernode      //顶点结点，为每一条邻接表的表头结点
 {
     int vex;    //当前定点编号
     arcnode * firarc;   //与该顶点相连的第一个顶点组成的边
 }Ver[maxn];

 void Init()  //建立图的邻接表需要先初始化，建立顶点结点
 {
     for(int i = 1; i <= n; i++)
     {
         Ver[i].vex = i;
         Ver[i].firarc = NULL;
     }
 }

 void Insert(int a, int b, int w)  //尾插法，插入以a为起点，b为终点，权为w的边，效率不如头插，但是可以去重边
 {
     arcnode * q = new arcnode(b, w);
     if(Ver[a].firarc == NULL)
         Ver[a].firarc = q;
     else
     {
         arcnode * p = Ver[a].firarc;
         if(p->vertex == b)
         {
             if(p->weight > w)
                 p->weight = w;
             return ;
         }
         while(p->next != NULL)
         {
             if(p->next->vertex == b)
             {
                 if(p->next->weight > w);
                     p->next->weight = w;
                 return ;
             }
             p = p->next;
         }
         p->next = q;
     }
 }
 void Insert2(int a, int b, int w)   //头插法，效率更高，但不能去重边
 {
     arcnode * q = new arcnode(b, w);
     if(Ver[a].firarc == NULL)
         Ver[a].firarc = q;
     else
     {
         arcnode * p = Ver[a].firarc;
         q->next = p;
         Ver[a].firarc = q;
     }
 }
 struct node     //保存key值的结点
 {
     int v;
     int key;
     friend bool operator<(node a, node b)   //自定义优先级，key小的优先
     {
         return a.key > b.key;
     }
 };

 #define INF 0xfffff    //权值上限
 int parent[maxn];   //每个结点的父节点
 bool visited[maxn]; //是否已经加入树种
 node vx[maxn];      //保存每个结点与其父节点连接边的权值
 priority_queue q; //优先队列stl实现
 void Prim()    //s表示根结点
 {
     for(int i = 1; i <= n; i++) //初始化
     {
         vx[i].v = i;
         vx[i].key = INF;
         parent[i] = -1;
         visited[i] = false;
     }
     vx[1].key = 0;
     q.push(vx[1]);
     while(!q.empty())
     {
         node nd = q.top();  //取队首，记得赶紧pop掉
         q.pop();
         if(visited[nd.v])   //注意这一句的深意，避免很多不必要的操作
             continue;
         visited[nd.v] = true;
         arcnode * p = Ver[nd.v].firarc;
         while(p != NULL)    //找到所有相邻结点，若未访问，则入队列
         {
             if(!visited[p->vertex] && p->weight < vx[p->vertex].key)
             {
                 parent[p->vertex] = nd.v;
                 vx[p->vertex].key = p->weight;
                 vx[p->vertex].v = p->vertex;
                 q.push(vx[p->vertex]);
             }
             p = p->next;
         }
     }
 }

 int main()
 {
     int a, b ,w;
     cout << "输入n和m: ";
     cin >> n >> m;
     Init();
     cout << "输入所有的边:" << endl;
     while(m--)
     {
         cin >> a >> b >> w;
         Insert2(a, b, w);
         Insert2(b, a, w);
     }
     Prim();
     cout << "输出所有结点的父结点:" << endl;
     for(int i = 1; i <= n; i++)
         cout << parent[i] << " ";
     cout << endl;
     cout << "最小生成树权值为：";
     int cnt = 0;
     for(int i = 1; i <= n; i++)
         cnt += vx[i].key;
     cout << cnt << endl;
     return 0;
 }

当明确知道没有重边时，用Insert2()进行插入能提高效率），运行结果如下（基于第一个例子）：

可用下列题进行测试：HDU搜索“畅通工程” POJ 1251
接下来是邻接矩阵实现Prim，非常简单，但是有几点还是需要注意的：

 #include
 #include
 #include
 using namespace std;

 #define maxn 110
 #define INF 100020    //预定于的最大值
 int n;   //顶点数、边数
 int g[maxn][maxn];      //邻接矩阵表示

 struct node     //保存key值的结点
 {
     int v;
     int key;
     friend bool operator<(node a, node b)   //自定义优先级，key小的优先
     {
         return a.key > b.key;
     }
 };
 int parent[maxn];   //每个结点的父节点
 bool visited[maxn]; //是否已经加入树种
 node vx[maxn];      //保存每个结点与其父节点连接边的权值
 priority_queue q; //优先队列stl实现
 void Prim()    //s表示根结点
 {
     for(int i = 1; i <= n; i++) //初始化
     {
         vx[i].v = i;
         vx[i].key = INF;
         parent[i] = -1;
         visited[i] = false;
     }
     vx[1].key = 0;
     q.push(vx[1]);
     while(!q.empty())
     {
         node nd = q.top();  //取队首，记得赶紧pop掉
         q.pop();
         if(visited[nd.v] == true)   //深意，因为push机器的可能是重复但是权值不同的点，我们只取最小的
             continue;
         int st = nd.v;
         //cout << nd.v << " " << nd.key << endl;
         visited[nd.v] = true;
         for(int j = 1;  j <= n; j++)
         {
             if(j!=st && !visited[j] && g[st][j] < vx[j].key)    //判断
             {
                 parent[j] = st;
                 vx[j].key = g[st][j];
                 q.push(vx[j]);

             }
         }
     }
 }
 int main()
 {
     while(~scanf("%d", &n))　　//点的个数
     {
         for(int i = 1; i <= n; i++)　　//输入邻接矩阵
             for(int j = 1; j <= n; j++)
             {
                 scanf("%d", &g[i][j]);
                 if(g[i][j] == 0)
                     g[i][j] = INF;　　//注意0的地方置为INF
             }
         Prim();　　//调用
         int ans = 0;　　//权值和
         for(int i = 1; i <= n; i++)
             ans += vx[i].key;
         printf("%d\n", ans);

     }
     return 0;
 }

最小生成树之prim算法

边赋以权值的图称为网或带权图，带权图的生成树也是带权的，生成树T各边的权值总和称为该树的权。

   最小生成树（MST）：权值最小的生成树。

   生成树和最小生成树的应用：要连通n个城市需要n－1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。

   构造网的最小生成树必须解决下面两个问题：

    1、尽可能选取权值小的边，但不能构成回路；

    2、选取n－1条恰当的边以连通n个顶点；

    MST性质：假设G＝(V,E)是一个连通网，U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中u∈U，v∈V－U，则必存在一棵包含边(u,v)的最小生成树。 

1.prim算法

  基本思想：假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

   在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

   此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

   Prim算法的核心:始终保持TE中的边集构成一棵生成树。

注意：prim算法适合稠密图，其时间复杂度为O(n^2)，其时间复杂度与边得数目无关，而kruskal算法的时间复杂度为O(eloge)跟边的数目有关，适合稀疏图。

看了上面一大段文字是不是感觉有点晕啊，为了更好理解我在这里举一个例子，示例如下：

 

（1）图中有6个顶点v1-v6，每条边的边权值都在图上；在进行prim算法时，我先随意选择一个顶点作为起始点，当然我们一般选择v1作为起始点，好，现在我们设U集合为当前所找到最小生成树里面的顶点，TE集合为所找到的边，现在状态如下：

U={v1}； TE={}；

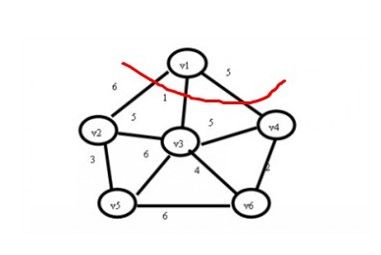
（2）现在查找一个顶点在U集合中，另一个顶点在V-U集合中的最小权值，如下图，在红线相交的线上找最小值。

通过图中我们可以看到边v1-v3的权值最小为1，那么将v3加入到U集合，（v1，v3）加入到TE，状态如下：

U={v1，v3}； TE={（v1，v3）}；

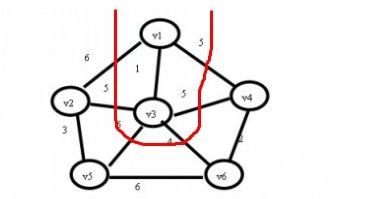
（3）继续寻找，现在状态为U={v1，v3}； TE={（v1，v3）}；在与红线相交的边上查找最小值。

我们可以找到最小的权值为（v3，v6）=4，那么我们将v6加入到U集合，并将最小边加入到TE集合，那么加入后状态如下：

U={v1，v3，v6}； TE={（v1，v3），（v3，v6）}； 如此循环一下直到找到所有顶点为止。

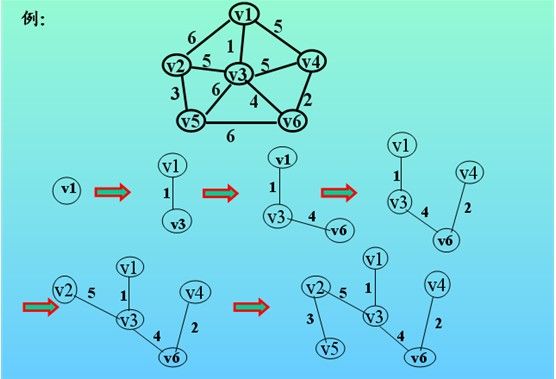
（4）下图像我们展示了全部的查找过程：