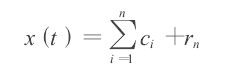心电信号去噪4--经验模拟分解法(EMD)

本系列上一篇(数学形态学)指路：https://blog.csdn.net/m0_37422217/article/details/90744326

注：这里是以小型手持心电图机为研究对象的(单导联)

上一篇中我们说到数学形态法可以很好的去除基线漂移和其他类型的噪音。这里我们介绍由，N. E. Huang 等人提出了经验模态分解（Empirical Mode Decomposition, EMD）方法。

 

EMD原理

这是一种可以将任何复杂信号分解为有限个固有模态函数（Instrinic Mode Function, IMF）的自适应、高效率的分解方法。经验模态分解适用于处理非线性和非平稳信号，例如心电信号，它有助于我们从很多方面理解信号的物理意义。

EMD对信号分解的原理是：把信号x(t)分解成一组内蕴模态函数(IMF)和一个最后的剩余值的和：

 

得到IMFs 的迭代过程需要满足两个条件：

（1）整个数据段内的零点数和极点数相等或至多相差1；

（2）信号由局部极大值确定的包络线和由局部极小值确定的包络线均值为零，即信号关于时间轴对称[57]。心电信号由EMD算法分解为一个高频部分（第一个IMF）和低频部分（剩余值），低频部分又将分解为高频部分（第二个IMF）和低频部分（剩余值），重复执行此过程，直到剩余量变成单一稳定的信号。

对心电信号x(t)进行EMD分解的具体步骤为：

（1）找到信号x(t)的局部极大值和极小值点，用三次样条插值计算出上、下包络线xu(t)和xl(t)；

（2）计算上下包络线的平均值m1(t)=(xu(t)+xl(t))/2，并计算x(t)和m1(t)的差值：d1(t)=x(t)-m1(t)；

（3）将d1(t)作为一个新的信号，重复第1步和第2步直到得到的心电信号满足上面的第一个IMF：c1(t)，剩余值r1(t)=x(t)-c1(t)；

（4）将r1(t)作为一个新的信号，重复前3步，得到多有的IMFs。当第n次的迭代rn(t)成为稳定的信号时，迭代过程就停止。信号x(t)的EMD分解完成。

 

实例

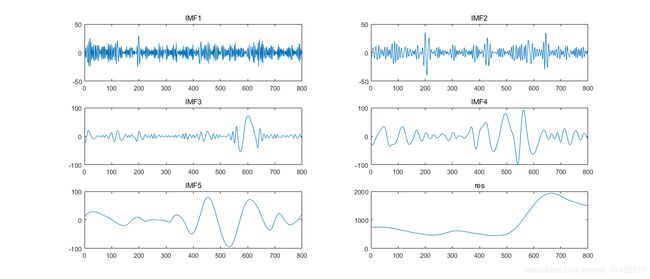
我们可以自己设定EMD的分解层数，这里我分解为5层：

代码：

OPTIONS.MAXMODES = 5; %设置IMF层数5层，得到的imf中有6行，最后一行为res.
[imf] = emd(x, OPTIONS); %EMD
subplot(3,2,1);plot(imf(1,:));title('IMF1');
subplot(3,2,2);plot(imf(2,:));title('IMF2');
subplot(3,2,3);plot(imf(3,:));title('IMF3');
subplot(3,2,4);plot(imf(4,:));title('IMF4');
subplot(3,2,5);plot(imf(5,:));title('IMF5');
subplot(3,2,6);plot(imf(6,:));title('res');

原始心电信号：

EMD分解：

可以看出随着层数的增加，频率在下降。

去噪方案

关于具体去噪方案，很多文献中都是利用组合算法，将心电信号进行EMD分解后，针对每一层的不同情况，结合小波阈值法和数学形态学等算法对其进行处理的。

比如：有文献指出，对高频噪声主导的IMF（如IMF1、IMF2等）进行类小波阈值处理，对有用信号主导的 IMF进行数学形态学滤波处理，最后对各处理后的IMF和残余分量重构，得到去除噪声的心电信号。

Matlab工具箱下载

这篇文章里有:https://blog.csdn.net/qrlhl/article/details/52213135

 

主要参考文献：

[1]基于EMD的心电信号去噪方法研究及实现验证

[2]EMD分解与IIR滤波器在心电信号预处理的应用研究

[3]基于改进EMD与形态滤波的齿轮故障特征提取

 

下一篇(小波及其他技术方面问题)指路：https://blog.csdn.net/m0_37422217/article/details/90951201