【转】如何防止softmax函数上溢出(overflow)和下溢出(underflow)
转载出处 :https://www.codelast.com/
《Deep Learning》(Ian Goodfellow & Yoshua Bengio & Aaron Courville)第四章「数值计算」中,谈到了上溢出(overflow)和下溢出(underflow)对数值计算的影响,并以softmax函数和log softmax函数为例进行了讲解。这里我再详细地把它总结一下。
『1』什么是下溢出(underflow)和上溢出(overflow)
实数在计算机内用二进制表示,所以不是一个精确值,当数值过小的时候,被四舍五入为0,这就是下溢出。此时如果对这个数再做某些运算(例如除以它)就会出问题。
反之,当数值过大的时候,情况就变成了上溢出。
『2』softmax函数是什么
softmax函数如下:
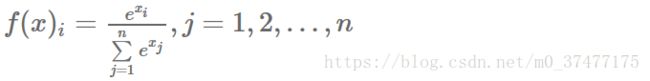
从公式上看含义不是特别清晰,所以借用知乎上的一幅图来说明(感谢原作者):

这幅图极其清晰地表明了softmax函数是什么,一图胜千言。
『2』计算softmax函数值的问题
通常情况下,计算softmax函数值不会出现什么问题,例如,当softmax函数表达式里的所有 xi 都是一个“一般大小”的数值 c 时——也就是上图中, z1=z2=z3=c z 1 = z 2 = z 3 = c 时,那么,计算出来的函数值 y1=y2=y3=13 y 1 = y 2 = y 3 = 1 3
但是,当某些情况发生时,计算函数值就出问题了:
- c 极其大,导致分子计算 ec e c 时上溢出。
- c 为负数,且 |c|很大,此时分母是一个极小的正数,有可能四舍五入为0,导致下溢出。
『3』如何解决
所以怎样所以怎样规避这些问题呢?我们可以用同一个方法一口气解决俩:
令 M = max( xi x i ), i =1,2,3,….,n,即M为所有 xi x i 中最大的值,那么我们只需要计算f( xi x i - M)的值,就可以解决上溢出、下溢出的问题了,并且,计算结果理论上仍然和 f(xi) f ( x i ) 保持一致。
举个实例:还是以前面的图为例,本来我们计算 f(z2) f ( z 2 ) 是用“常规”方法来算的:
ez2ez1+ez2+ez3 e z 2 e z 1 + e z 2 + e z 3 = e1e3+e1+e−3≈0.12 e 1 e 3 + e 1 + e − 3 ≈ 0.12
ez2ez1+ez2+ez3 e z 2 e z 1 + e z 2 + e z 3 = ez2eMez1eM+ez2eM+ez3eM=e1−3e1−3+e3−3+e−3−3≈0.12 e z 2 e M e z 1 e M + e z 2 e M + e z 3 e M = e 1 − 3 e 1 − 3 + e 3 − 3 + e − 3 − 3 ≈ 0.12
其中,
M=3是 z1,z2,z3 z 1 , z 2 , z 3 中的最大值。可见计算结果并未改变。
通过这样的变换,对任何一个 xi,减去M之后,e 的指数的最大值为0,所以不会发生上溢出;同时,分母中也至少会包含一个值为1的项,所以分母也不会下溢出(四舍五入为0)。
所以这个技巧没什么高级的技术含量。
『4』延伸问题
看似已经结案了,但仍然有一个问题:如果softmax函数中的分子发生下溢出,也就是前面所说的 c 为负数,且 |c|很大,此时分母是一个极小的正数,有可能四舍五入为0的情况,此时,如果我们把softmax函数的计算结果再拿去计算 log,即 log softmax,其实就相当于计算 log(0),所以会得到 −∞,但这实际上是错误的,因为它是由舍入误差造成的计算错误。所以,有没有一个方法,可以把这个问题也解决掉呢?答案还是采用和前面类似的策略来计算 log softmax 函数值:
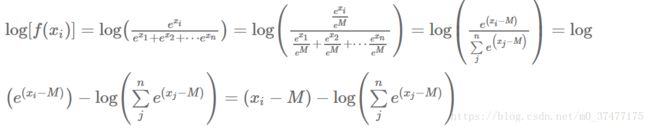
大家看到,在最后的表达式中,会产生下溢出的因素已经被消除掉了——求和项中,至少有一项的值为1,这使得log后面的值不会下溢出,也就不会发生计算 log(0) 的悲剧。