tf-openpose人体姿态估计标签生成--heatmap--vectormap

项目地址：https://github.com/ildoonet/tf-pose-estimation

人体姿态估计部分代码解读

前言

openpose是自下而上的人体姿态估计方法，此处我们讨论的是tensorflow的版本。
coco keypoints 标注 以及tf-openpose的标注调整如下图所示(调整顺序为了适应PAF阶段的预测)：

序号	coco ori	openpose
1	鼻子	鼻子
2	左眼	脖颈
3	右眼	右肩
4	左耳	右肘
5	右耳	右手
6	左肩	左肩
7	右肩	左肘
8	左肘	左手
9	右肘	右髋
10	左手	右膝
11	右手	右脚
12	左髋	左髋
13	右髋	左膝
14	左膝	左脚
15	右膝	右眼
16	左脚	左眼
17	右脚	右耳
18		左耳

其中脖颈为左肩和右肩的中点！

heatmap高斯分布生成代码（pose_dataset.py）

函数get_heatmap生成关键点热力图，未在图内且未标注的关键点生成的heatmap所有值都为0。一共19个heatmap，其中最后一个代表背景，

def get_heatmap(self, target_size):
    heatmap = np.zeros((CocoMetadata.__coco_parts, self.height, self.width), dtype=np.float32)
    ##全部heatmap都初始化为0
    for joints in self.joint_list:
        for idx, point in enumerate(joints):
            if point[0] < 0 or point[1] < 0: 
                continue
            CocoMetadata.put_heatmap(heatmap, idx, point, self.sigma)
    heatmap = heatmap.transpose((1, 2, 0)) ##self.height, self.width, CocoMetadata.__coco_parts,
    # background
    heatmap[:, :, -1] = np.clip(1 - np.amax(heatmap, axis=2), 0.0, 1.0)  
    if target_size:
        heatmap = cv2.resize(heatmap, target_size, interpolation=cv2.INTER_AREA) #插值resize
    return heatmap.astype(np.float16)

注：
1. numpy.clip(a, a_min, a_max, out=None) ：clip这个函数将将数组中的元素限制在a_min,
a_max之间，大于a_max的就使得它等于 a_max，小于a_min,的就使得它等于a_min。

函数put_heatmap单个关键点keypoints热力图生成

def put_heatmap(heatmap, plane_idx, center, sigma):
    center_x, center_y = center
    _, height, width = heatmap.shape[:3]
    th = 4.6052
    delta = math.sqrt(th * 2)

    x0 = int(max(0, center_x - delta * sigma))
    y0 = int(max(0, center_y - delta * sigma))

    x1 = int(min(width, center_x + delta * sigma))
    y1 = int(min(height, center_y + delta * sigma))

    for y in range(y0, y1):
        for x in range(x0, x1):
            d = (x - center_x) ** 2 + (y - center_y) ** 2  ###高斯！！
            exp = d / 2.0 / sigma / sigma  ##高斯！！
            if exp > th:
                continue
            heatmap[plane_idx][y][x] = max(heatmap[plane_idx][y][x], math.exp(-exp))
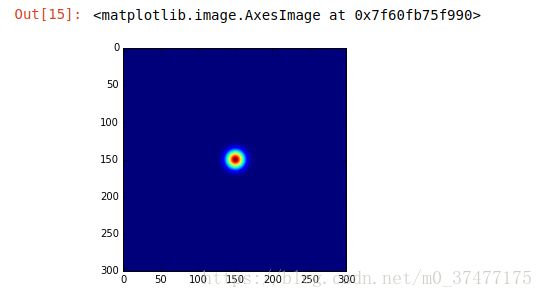
            heatmap[plane_idx][y][x] = min(heatmap[plane_idx][y][x], 1.0)

一个关键点的测试效果（高斯分布）：

vectormap 向量叉乘生成代码（pose_dataset.py）

函数get_vetormap得到PAF标签，vectormap是heatmap的两倍为38个（19*2），因为有19条的关键点连接线，每一条线使用向量表示，分别有x维度的map,以及y轴的map。
此处map上的区域赋值，要限定区域使用的是向量的叉乘：

    def get_vectormap(self, target_size):
        vectormap = np.zeros((CocoMetadata.__coco_parts*2, self.height, self.width), dtype=np.float32)
        countmap = np.zeros((CocoMetadata.__coco_parts, self.height, self.width), dtype=np.int16)
        for joints in self.joint_list:
            for plane_idx, (j_idx1, j_idx2) in enumerate(CocoMetadata.__coco_vecs):
                j_idx1 -= 1
                j_idx2 -= 1
                center_from = joints[j_idx1]
                center_to = joints[j_idx2]

                if center_from[0] < -100 or center_from[1] < -100 or center_to[0] < -100 or center_to[1] < -100:
                    continue
                CocoMetadata.put_vectormap(vectormap, countmap, plane_idx, center_from, center_to)
        vectormap = vectormap.transpose((1, 2, 0))
        nonzeros = np.nonzero(countmap)
        for p, y, x in zip(nonzeros[0], nonzeros[1], nonzeros[2]):
            if countmap[p][y][x] <= 0:
                continue
            vectormap[y][x][p*2+0] /= countmap[p][y][x]
            vectormap[y][x][p*2+1] /= countmap[p][y][x]

        if target_size:
            vectormap = cv2.resize(vectormap, target_size, interpolation=cv2.INTER_AREA)

        return vectormap.astype(np.float16)

函数put_vectormap得到单个向量的map（2个）表示。

  def put_vectormap(vectormap, countmap, plane_idx, center_from, center_to, threshold=8):
        _, height, width = vectormap.shape[:3]

        vec_x = center_to[0] - center_from[0]
        vec_y = center_to[1] - center_from[1]
        min_x = max(0, int(min(center_from[0], center_to[0]) - threshold))
        min_y = max(0, int(min(center_from[1], center_to[1]) - threshold))

        max_x = min(width, int(max(center_from[0], center_to[0]) + threshold))
        max_y = min(height, int(max(center_from[1], center_to[1]) + threshold))
        norm = math.sqrt(vec_x ** 2 + vec_y ** 2)
        if norm == 0:
            return

        vec_x /= norm
        vec_y /= norm

        for y in range(min_y, max_y):
            for x in range(min_x, max_x):
                bec_x = x - center_from[0]
                bec_y = y - center_from[1]
                dist = abs(bec_x * vec_y - bec_y * vec_x)  ##向量叉乘根据阈值选择赋值区域
                if dist > threshold:
                    continue

                countmap[plane_idx][y][x] += 1

                vectormap[plane_idx*2+0][y][x] = vec_x
                vectormap[plane_idx*2+1][y][x] = vec_y

vec_x 以及 vec_y为单位向量，任何向量与单位向量的叉乘即为四边形的面积

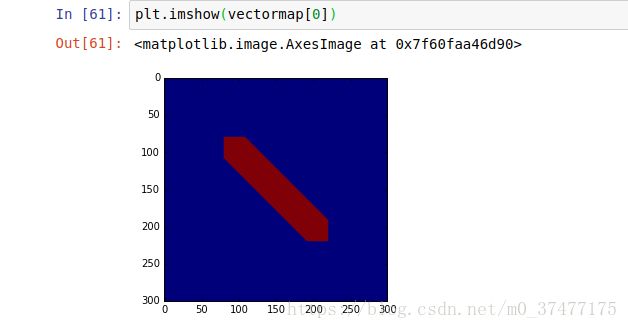
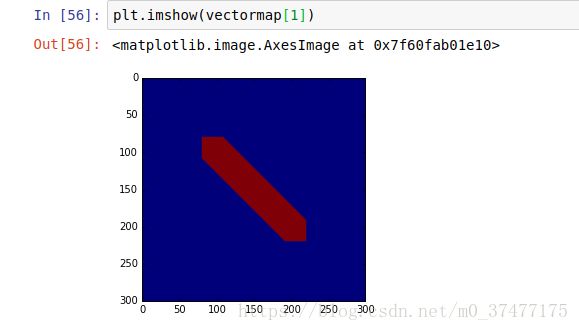
两个点的vectmap标注示意：

vec x

vex y

向量叉乘

首先简单讲讲向量：向量是一种既有方向、又有大小的量（如一个箭头表示就很形象），在平面直角坐标系中，若A的坐标为(x,y)，B的坐标为

(x0,y0) ( x 0 , y 0 )

，则向量AB的方向由A指向B，用

(x0−x,y0−y) ( x 0 − x , y 0 − y )

表示。
定义：叉乘是向量间的一种运算，设两个向量分别为

(x1,y1),(x2,y2) ( x 1 , y 1 ) , ( x 2 , y 2 )

，那么它们的叉乘就为 (x1∗y2−x2∗y1) ( x 1 ∗ y 2 − x 2 ∗ y 1 ) ，它也是一个向量，但在本文中，我们不讨论它的方向。
几何意义：
叉乘的几何意义是以两向量为邻边的平行四边形的有向面积!!

由上图所示，向量由一条起点出发到达另一条平行线（角度小于90度），此向量与其中一条的平行线单位向量进行叉乘，得到的四边形面积保持不变！！从而限定了向量赋值的区域！最后得到的限定区域为下图的六边形。

参考资料：
1.数学基础 —— 向量运算（叉乘)