从loss处理图像分割中类别极度不均衡的状况---keras
文章目录
- 前言
- 场景
- loss function
- 一、Log loss
- 二、WBE Loss
- 三、Focal loss
- 四、Dice loss
- 五、IOU loss
- 六、Tversky loss
- 七、敏感性--特异性 loss
- 八、Generalized Dice loss
- 九、BCE + Dice loss
- 十、Dice + Focal loss
- 十一、Exponential Logarithmic loss
- 参考
前言
最近在做小目标图像分割任务(医疗方向),往往一幅图像中只有一个或者两个目标,而且目标的像素比例比较小,使网络训练较为困难,一般可能有三种的解决方式:
- 选择合适的loss function,对网络进行合理的优化,关注较小的目标。
- 改变网络结构,使用attention机制(类别判断作为辅助)。
- 与2的根本原理一致,类属attention,即:先检测目标区域,裁剪之后进行分割训练。
通过使用设计合理的loss function,相比于另两种方式更加简单易行,能够保留图像所有信息的情况下进行网络优化,达到对小目标精确分割的目的。
场景
loss function
一、Log loss
对于二分类而言,对数损失函数如下公式所示: − 1 N ∑ i = 1 N ( y i log p i + ( 1 − y i ) log ( 1 − p i ) ) -\frac{1}{N}\sum_{i=1}^{N}(y_i\log p_i + (1-y_i)\log (1-p_i)) −N1i=1∑N(yilogpi+(1−yi)log(1−pi))
其中, y i y_i yi为输入实例 x i x_i xi的真实类别, p i p_i pi为预测输入实例 x i x_i xi 属于类别 1 的概率. 对所有样本的对数损失表示对每个样本的对数损失的平均值, 对于完美的分类器, 对数损失为 0。
此loss function每一次梯度的回传对每一个类别具有相同的关注度!所以极易受到类别不平衡的影响,在图像分割领域尤其如此。
例如目标在整幅图像当中占比也就仅仅千分之一,那么在一副图像中,正样本(像素点)与父样本的比例约为1~1000,如果训练图像中还包含大量的背景图,即图像当中不包含任何的疾病像素,那么不平衡的比例将扩大到>10000,那么训练的后果将会是,网络倾向于什么也不预测!生成的mask几乎没有病灶像素区域!
此处的案例可以参考airbus-ship-detection。
二、WBE Loss
带权重的交叉熵loss — Weighted cross-entropy (WCE)[6]
R为标准的分割图,其中 r n r_n rn为label 分割图中的某一个像素的GT。P为预测的概率图, p n p_n pn为像素的预测概率值,背景像素图的概率值就为1-P。
只有两个类别的带权重的交叉熵为:
W C E = − 1 N ∑ n = 1 N w r n l o g ( p n ) + ( 1 − r n ) l o g ( 1 − p n ) WCE = - \frac{1}{N}\sum_{n=1}^{N}wr_nlog(p_n) + (1 - r_n)log(1 - p_n) WCE=−N1n=1∑Nwrnlog(pn)+(1−rn)log(1−pn)
w w w为权重, w = N − ∑ n p n ∑ n p n w=\frac{N-\sum_np_n}{\sum_np_n} w=∑npnN−∑npn
缺点是需要人为的调整困难样本的权重,增加调参难度。
三、Focal loss
能否使网络主动学习困难样本呢?
focal loss的提出是在目标检测领域,为了解决正负样本比例严重失衡的问题。是由log loss改进而来的,为了于log loss进行对比,公式如下:
− 1 N ∑ i = 1 N ( α y i ( 1 − p i ) γ log p i + ( 1 − α ) ( 1 − y i ) p i γ log ( 1 − p i ) ) -\frac{1}{N}\sum_{i=1}^{N}(\alpha y_i(1-p_i)^{\gamma}\log p_i + (1-\alpha )(1-y_i)p_i^{\gamma}\log (1-p_i)) −N1i=1∑N(αyi(1−pi)γlogpi+(1−α)(1−yi)piγlog(1−pi))
说白了就多了一个 ( 1 − p i ) γ (1-p_i)^{\gamma} (1−pi)γ,loss随样本概率的大小如下图所示:

其基本思想就是,对于类别极度不均衡的情况下,网络如果在log loss下会倾向于只预测负样本,并且负样本的预测概率 p i p_i pi也会非常的高,回传的梯度也很大。但是如果添加 ( 1 − p i ) γ (1-p_i)^{\gamma} (1−pi)γ则会使预测概率大的样本得到的loss变小,而预测概率小的样本,loss变得大,从而加强对正样本的关注度。
可以改善目标不均衡的现象,对此情况比 binary_crossentropy 要好很多。
目前在图像分割上只是适应于二分类。
代码:https://github.com/mkocabas/focal-loss-keras
from keras import backend as K
'''
Compatible with tensorflow backend
'''
def focal_loss(gamma=2., alpha=.25):
def focal_loss_fixed(y_true, y_pred):
pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred))
pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
return -K.sum(alpha * K.pow(1. - pt_1, gamma) * K.log(pt_1))-K.sum((1-alpha) * K.pow( pt_0, gamma) * K.log(1. - pt_0))
return focal_loss_fixed
使用方法:
model_prn.compile(optimizer=optimizer, loss=[focal_loss(alpha=.25, gamma=2)])
目前实验得到结论:
- 经过测试,发现使用focal loss很容易就会过拟合??且效果一般。。。I don’t know why?
- 此方法代码有待改进,因为此处使用的网络为U-net,输入和输出都是一张图!直接使用会导致loss的值非常的大!
- 需要添加额外的两个全局参数alpha和gamma,对于调参不方便。
以上的方法Log loss,WBE Loss,Focal loss都是从本源上即从像素上来对网络进行优化。针对的都是像素的分类正确与否。有时并不能在评测指标上DICE上得到较好的结果。
四、Dice loss
dice loss 的提出是在V-net中,其中的一段原因描述是在感兴趣的解剖结构仅占据扫描的非常小的区域,从而使学习过程陷入损失函数的局部最小值。所以要加大前景区域的权重。
Dice 可以理解为是两个轮廓区域的相似程度,用A、B表示两个轮廓区域所包含的点集,定义为:
D S C ( A , B ) = 2 ∣ A ⋂ B ∣ ∣ A ∣ + ∣ B ∣ DSC(A,B) = 2\frac{|A\bigcap B |}{|A| + |B|} DSC(A,B)=2∣A∣+∣B∣∣A⋂B∣
其次Dice也可以表示为:
D S C = 2 T P 2 T P + F N + F P DSC = \frac{2TP}{2TP+FN+FP} DSC=2TP+FN+FP2TP
其中TP,FP,FN分别是真阳性、假阳性、假阴性的个数。
二分类dice loss:
D L 2 = 1 − ∑ n = 1 N p n r n + ϵ ∑ n = 1 N p n + r n + ϵ − ∑ n = 1 N ( 1 − p n ) ( 1 − r n ) + ϵ ∑ n = 1 N 2 − p n − r n + ϵ DL_2 = 1 - \frac{\sum_{n=1}^{N}p_nr_n + \epsilon}{\sum_{n=1}^{N}p_n + r_n + \epsilon} -\frac{\sum_{n=1}^{N}(1 - p_n)(1 - r_n) + \epsilon}{\sum_{n=1}^{N}2 - p_n - r_n + \epsilon} DL2=1−∑n=1Npn+rn+ϵ∑n=1Npnrn+ϵ−∑n=1N2−pn−rn+ϵ∑n=1N(1−pn)(1−rn)+ϵ
代码:
def dice_coef(y_true, y_pred, smooth=1):
intersection = K.sum(y_true * y_pred, axis=[1,2,3])
union = K.sum(y_true, axis=[1,2,3]) + K.sum(y_pred, axis=[1,2,3])
return K.mean( (2. * intersection + smooth) / (union + smooth), axis=0)
def dice_coef_loss(y_true, y_pred):
1 - dice_coef(y_true, y_pred, smooth=1)
结论:
- 有时使用dice loss会使训练曲线有时不可信,而且dice loss好的模型并不一定在其他的评价标准上效果更好,例如mean surface distance 或者是Hausdorff surface distance。
不可信的原因是梯度,对于softmax或者是log loss其梯度简化而言为 p − t p-t p−t, t t t为目标值, p p p为预测值。而dice loss为 2 t 2 ( p + t ) 2 \frac{2t^2}{(p+t)^2} (p+t)22t2,如果 p p p, t t t过小则会导致梯度变化剧烈,导致训练困难。 - 属于直接在评价标准上进行优化。
- 不均衡的场景下的确好使。
论文中在前列腺MRI容积图中的分割表现:
五、IOU loss
可类比DICE LOSS,也是直接针对评价标准进行优化[11]。
在图像分割领域评价标准IOU实际上 I O U = T P T P + F P + F N IOU = \frac{TP}{TP + FP + FN} IOU=TP+FP+FNTP,而TP,FP,FN分别是真阳性、假阳性、假阴性的个数。
而作为loss function,定义 I O U = I ( X ) U ( X ) IOU = \frac{I(X)}{U(X)} IOU=U(X)I(X),其中, I ( X ) = X ∗ Y I(X) = X*Y I(X)=X∗Y
U ( X ) = X + Y − X ∗ Y U(X) = X + Y - X*Y U(X)=X+Y−X∗Y,X为预测值而Y为真实标签。
## intersection over union
def IoU(y_true, y_pred, eps=1e-6):
if np.max(y_true) == 0.0:
return IoU(1-y_true, 1-y_pred) ## empty image; calc IoU of zeros
intersection = K.sum(y_true * y_pred, axis=[1,2,3])
union = K.sum(y_true, axis=[1,2,3]) + K.sum(y_pred, axis=[1,2,3]) - intersection
return -K.mean( (intersection + eps) / (union + eps), axis=0)
[11]在PASCAL VOC 2010上的实验效果如下,基础框架还是FCN

IOU loss的缺点呢同DICE loss是相类似的,训练曲线可能并不可信,训练的过程也可能并不稳定,有时不如使用softmax loss等的曲线有直观性,通常而言softmax loss得到的loss下降曲线较为平滑。
六、Tversky loss
提到Tversky loss不得不提Tversky 系数,Tversky系数是Dice系数和 Jaccard 系数的一种广义系数,公式如下:
T ( A , B ) = ∣ A ⋂ B ∣ ∣ A ⋂ B ∣ + α ∣ A − B ∣ + β ∣ B − A ∣ T(A,B) = \frac{|A \bigcap B|}{|A \bigcap B| + \alpha |A - B| + \beta |B - A|} T(A,B)=∣A⋂B∣+α∣A−B∣+β∣B−A∣∣A⋂B∣
再抄一遍Dice系数公式:
D S C ( A , B ) = 2 ∣ A ⋂ B ∣ ∣ A ∣ + ∣ B ∣ DSC(A,B) = 2\frac{|A\bigcap B |}{|A| + |B|} DSC(A,B)=2∣A∣+∣B∣∣A⋂B∣,此时A为预测,而B为真实标签。
观察可得当设置 α = β = 0.5 \alpha = \beta = 0.5 α=β=0.5,此时Tversky系数就是Dice系数。而当设置 α = β = 1 \alpha = \beta = 1 α=β=1时,此时Tversky系数就是Jaccard系数。
对于Tversky loss也是相似的形式就不重新编写了,但是在 T ( A , B ) T(A,B) T(A,B)中, ∣ A − B ∣ |A - B| ∣A−B∣则意味着是FP(假阳性),而 ∣ B − A ∣ |B - A| ∣B−A∣则意味着是FN(假阴性); α 和 β \alpha和 \beta α和β分别控制假阴性和假阳性。通过调整 α \alpha α和 β \beta β我们可以控制假阳性和假阴性之间的权衡。
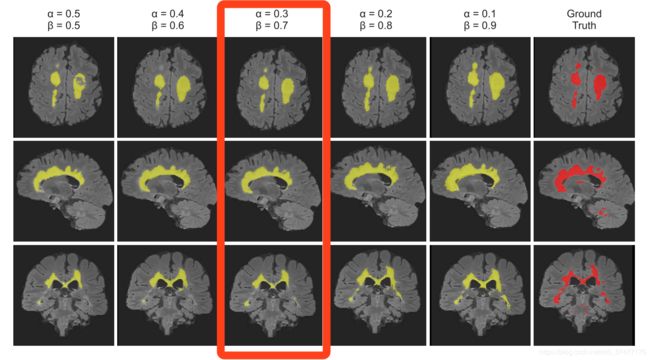
不同的 α \alpha α和 β \beta β下各个指标的结果:

在极小的病灶下的分割效果图如下:
在较大病灶下的分割结果:
考虑到处理数据类别极度不均衡情况下的指标FP和FN,在牺牲一定精度的情况下,从而提高像素分类的召回率。
代码参考keras
def tversky(y_true, y_pred):
y_true_pos = K.flatten(y_true)
y_pred_pos = K.flatten(y_pred)
true_pos = K.sum(y_true_pos * y_pred_pos)
false_neg = K.sum(y_true_pos * (1-y_pred_pos))
false_pos = K.sum((1-y_true_pos)*y_pred_pos)
alpha = 0.7
return (true_pos + smooth)/(true_pos + alpha*false_neg + (1-alpha)*false_pos + smooth)
def tversky_loss(y_true, y_pred):
return 1 - tversky(y_true,y_pred)
def focal_tversky(y_true,y_pred):
pt_1 = tversky(y_true, y_pred)
gamma = 0.75
return K.pow((1-pt_1), gamma)
七、敏感性–特异性 loss
首先敏感性就是召回率,检测出确实有病的能力:
S e n s i t i v i t y = T P T P + F N Sensitivity = \frac{TP}{TP+FN} Sensitivity=TP+FNTP
特异性,检测出确实没病的能力:
S p e c i f i c i t y = T N T N + F P Specificity = \frac{TN}{TN+FP} Specificity=TN+FPTN
Sensitivity - Specificity (SS)[8]提出是在:
S S = λ ∑ n = 1 N ( r n − p n ) 2 r n ∑ n = 1 N r n + ϵ + ( 1 − λ ) ∑ n = 1 N ( r n − p n ) 2 ( 1 − r n ) ∑ n = 1 N ( 1 − r n ) + ϵ SS = \lambda\frac{\sum_{n=1}^{N}(r_n - p_n)^2r_n}{\sum_{n=1}^{N}r_n + \epsilon} + (1 - \lambda)\frac{\sum_{n=1}^{N}(r_n - p_n)^2(1 - r_n)}{\sum_{n=1}^{N}(1 - r_n) + \epsilon} SS=λ∑n=1Nrn+ϵ∑n=1N(rn−pn)2rn +(1−λ)∑n=1N(1−rn)+ϵ∑n=1N(rn−pn)2(1−rn)
其中左边为病灶像素的错误率即, 1 − S e n s i t i v i t y 1- Sensitivity 1−Sensitivity,而不是正确率,所以设置λ 为0.05。其中 ( r n − p n ) 2 (r_n - p_n)^2 (rn−pn)2是为了得到平滑的梯度。
八、Generalized Dice loss
区域大小和Dice分数之间的相关性:
在使用DICE loss时,对小目标是十分不利的,因为在只有前景和背景的情况下,小目标一旦有部分像素预测错误,那么就会导致Dice大幅度的变动,从而导致梯度变化剧烈,训练不稳定。
首先Generalized Dice loss的提出是源于Generalized Dice index[12]。当病灶分割有多个区域时,一般针对每一类都会有一个DICE,而Generalized Dice index将多个类别的dice进行整合,使用一个指标对分割结果进行量化。
GDL(the generalized Dice loss)公式如下(标签数量为2):
G D L = 1 − 2 ∑ l = 1 2 w l ∑ n r l n p l n ∑ l = 1 2 w l ∑ n r l n + p l n GDL = 1 - 2\frac{\sum_{l=1}^{2}w_l\sum_nr_{ln}p_{ln}}{\sum_{l=1}^{2}w_l\sum_nr_{ln} + p_{ln}} GDL=1−2∑l=12wl∑nrln+pln∑l=12wl∑nrlnpln
其中 r l n r_{ln} rln为类别l在第n个像素的标准值(GT),而 p l n p_{ln} pln为相应的预测概率值。此处最关键的是 w l w_l wl,为每个类别的权重。其中 w l = 1 ( ∑ n = 1 N r l n ) 2 w_l = \frac{1}{(\sum_{n=1}^{N}r_{ln})^2} wl=(∑n=1Nrln)21,这样,GDL就能平衡病灶区域和Dice系数之间的平衡。
论文中的一个效果:

但是在AnatomyNet中提到GDL面对极度不均衡的情况下,训练的稳定性仍然不能保证。
参考代码:
def generalized_dice_coeff(y_true, y_pred):
Ncl = y_pred.shape[-1]
w = K.zeros(shape=(Ncl,))
w = K.sum(y_true, axis=(0,1,2))
w = 1/(w**2+0.000001)
# Compute gen dice coef:
numerator = y_true*y_pred
numerator = w*K.sum(numerator,(0,1,2,3))
numerator = K.sum(numerator)
denominator = y_true+y_pred
denominator = w*K.sum(denominator,(0,1,2,3))
denominator = K.sum(denominator)
gen_dice_coef = 2*numerator/denominator
return gen_dice_coef
def generalized_dice_loss(y_true, y_pred):
return 1 - generalized_dice_coeff(y_true, y_pred)
以上本质上都是根据评测标准设计的loss function,有时候普遍会受到目标太小的影响,导致训练的不稳定;对比可知,直接使用log loss等的loss曲线一般都是相比较光滑的。
九、BCE + Dice loss
BCE : Binary Cross Entropy
说白了,添加二分类交叉熵损失函数。在数据较为平衡的情况下有改善作用,但是在数据极度不均衡的情况下,交叉熵损失会在几个训练之后远小于Dice 损失,效果会损失。
代码:
import keras.backend as K
from keras.losses import binary_crossentropy
def dice_coef(y_true, y_pred, smooth=1):
intersection = K.sum(y_true * y_pred, axis=[1,2,3]) ##y_true与y_pred都是矩阵!(Unet)
union = K.sum(y_true, axis=[1,2,3]) + K.sum(y_pred, axis=[1,2,3])
return K.mean( (2. * intersection + smooth) / (union + smooth), axis=0)
def dice_p_bce(in_gt, in_pred):
return 1e-3*binary_crossentropy(in_gt, in_pred) - dice_coef(in_gt, in_pred)
-------更新2018-11-8
keras.losses.binary_crossentropy
只沿最后一个轴进行计算[3]。因此,binary_crossentropy(y_true,y_pred)+ dice_loss(y_true,y_pred)仍将是(batch_size,height,width)张量。
改进:
K.mean(binary_crossentropy(y_true,y_pred))+ dice_loss(y_true,y_pred)
正确性有待验证。
思考:Dice + Focal loss ???
------------------更新2018-11-18
十、Dice + Focal loss
最近腾讯医疗AI新突破:提出器官神经网络,全自动辅助头颈放疗规划 | 论文[2] 中提出了Dice + Focal loss来处理小器官的分割问题。在前面的讨论也提到过,直接使用Dice会使训练的稳定性降低[1],而此处再添加上Focal loss这个神器。
首先根据论文的公式:
T P p ( c ) = ∑ n = 1 N p n ( c ) g n ( c ) TP_p(c) = \sum_{n=1}^{N}p_n(c)g_n(c) TPp(c)=n=1∑Npn(c)gn(c)
F N p ( c ) = ∑ n = 1 N ( 1 − p n ( c ) ) g n ( c ) FN_p(c) = \sum_{n=1}^{N}(1-p_n(c))g_n(c) FNp(c)=n=1∑N(1−pn(c))gn(c)
F P n ( c ) = ∑ n = 1 N p n ( c ) ( 1 − g n ( c ) ) FP_n(c) = \sum_{n=1}^{N}p_n(c)(1-g_n(c)) FPn(c)=n=1∑Npn(c)(1−gn(c))
L D i c e = ∑ c = 0 C T P n ( c ) T P p ( c ) + α F N p ( c ) + β F P p ( c ) − L_{Dice} = \sum_{c=0}^{C} \frac{TP_n(c)}{TP_p(c) + \alpha FN_p(c) + \beta FP_p(c)} - LDice=c=0∑CTPp(c)+αFNp(c)+βFPp(c)TPn(c)−
其中 T P p ( c ) , F N p ( c ) , F P p ( c ) TP_p(c) ,FN_p(c) ,FP_p(c) TPp(c),FNp(c),FPp(c),分别对于类别c的真阳性,假阴性,假阳性。此处的 α = β = 0.5 \alpha = \beta = 0.5 α=β=0.5,此时Tversky系数就是Dice系数,为Dice loss。
最终的loss为:
L = L D i c e + λ L F o c a l = C − ∑ c = 0 C T P n ( c ) T P p ( c ) + α F N p ( c ) + β F P p ( c ) − λ 1 N ∑ c = 0 C ∑ n = 1 N g n ( c ) ( 1 − p n ( c ) ) 2 l o g ( p n ( c ) ) L = L_{Dice} + \lambda L_{Focal} = C - \sum_{c=0}^{C} \frac{TP_n(c)}{TP_p(c) + \alpha FN_p(c) + \beta FP_p(c)} - \lambda \frac{1}{N} \sum_{c=0}^{C} \sum_{n=1}^{N}g_n(c)(1-p_n(c))^2log(p_n(c)) L=LDice+λLFocal=C−c=0∑CTPp(c)+αFNp(c)+βFPp(c)TPn(c)−λN1c=0∑Cn=1∑Ngn(c)(1−pn(c))2log(pn(c))
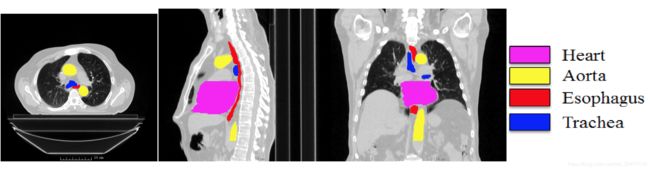
论文中头颈部癌症放疗靶区自动勾画效果展示:

项目地址
Focal loss理论上应该还是会得到很大的值?
十一、Exponential Logarithmic loss
与加权的DICE LOSS进行对比,此方法觉得而且这种情况跟不同标签之间的相对尺寸无关,但是可以通过标签频率来进行平衡[9]。
结合了focal loss以及Dice loss。此loss的公式如下:
L E X P = w d i c e ∗ L D i c e + w C r o s s ∗ L C r o s s L_{EXP} = w_{dice}*L_{Dice} + w_{Cross}*L_{Cross} LEXP=wdice∗LDice+wCross∗LCross L D i c e L_{Dice} LDice为 指数log Dice损失, L C r o s s L_{Cross} LCross为指数交叉熵损失。
L D i c e = E [ ( − l n ( D i c e i ) ) γ D i c e ] L_{Dice} = E[(-ln({Dice}_i))^{\gamma_{Dice}}] LDice=E[(−ln(Dicei))γDice]
i i i为label。
复习一下交叉熵损失:
L C E = − l o g ( p l ( x ) ) L_{CE} = -log(p_l(x)) LCE=−log(pl(x))
新的指数交叉熵损失:
L C r o s s = w l ( − l n ( p l ( x ) ) ) γ C r o s s L_{Cross} = w_l(-ln(p_l(x)))^{\gamma_{Cross}} LCross=wl(−ln(pl(x)))γCross
其中, w l = ( ∑ k f k f l ) 0.5 w_l = (\frac{\sum_kf_k}{f_l})^{0.5} wl=(fl∑kfk)0.5, f k f_k fk为标签k的出现频率, w l w_l wl这个参数可以减小出现频率较高的类别权重。由公式可知, w l w_l wl随 f l f_l fl的增大而变小,即减小权重,反之如果 f l f_l fl太大,那么权重会变小
γ D i c e \gamma_{Dice} γDice和 γ C r o s s \gamma_{Cross} γCross,提升非线性的作用。
如下图显示的是不同的指数log非线性表现:

新增添了4个参数权重分别是 w D i c e w_{Dice} wDice和 w C r o s s w_{Cross} wCross, γ D i c e \gamma_{Dice} γDice和 γ C r o s s \gamma_{Cross} γCross,给调参带来不小的麻烦。
以上都是针对多种loss的简单结合或者是加权结合,可能也有些小的改进,但如何平衡两个或者多个loss也是偏经验的调参问题。
如果有好的方式方法可以在此讨论:小目标的图像语义分割,有什么解决类别不平衡的方法吗?[5]
所有代码将整理到GitHub。
参考
[1] C. H. Sudre, W. Li, T. Vercauteren, S. Ourselin, and M. J. Cardoso, “Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations,” in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, 2017.
[2] AnatomyNet: Deep Learning for Fast and Fully Automated Whole-volume Segmentation of Head and Neck Anatomy: https://arxiv.org/pdf/1808.05238.pdf
[3] https://www.kaggle.com/c/airbus-ship-detection/discussion/70549
[4] https://www.kaggle.com/kmader/baseline-u-net-model-part-1
[5] 小目标的图像语义分割,有什么解决类别不平衡的方法吗?:https://www.zhihu.com/question/297255242/answer/505965855
[6] Generalised Dice overlap as a deep learning loss function for highly unbalanced segmentations-2017
[7] Ronneberger, O., Fischer, P., Brox, T.: U-net: Convolutional networks for biomedical image segmentation. In: MICCAI. pp. 234–241. Springer (2015)
[8] Brosch, T., Yoo, Y., Tang, L.Y., Li, D.K., Traboulsee, A., Tam, R.: Deep convolutional encoder networks for multiple sclerosis lesion segmentation. In: MICCAI 2015. pp. 3–11. Springer (2015)
[9]3D Segmentation with Exponential LogarithmicLoss for Highly Unbalanced Object Sizes-MICCAI2018【论文理解】
[10]Dice-coefficient loss function vs cross-entropy
[11]Md Atiqur Rahman and Yang Wang, Optimizing Intersection-Over-Union in Deep Neural Networks for Image Segmentation
[12]Crum, W., Camara, O., Hill, D.: Generalized Overlap Measures for Evaluation and Validation in Medical Image Analysis. IEEE TMI 25(11), 1451–1461 (nov 2006)