A Fast Learning Algorithm for Deep Belief Nets
题目: A Fast Learning Algorithm for Deep Belief Nets
作者: Geoffrey E. Hinton, Simon Osindero, Yee-Whye Teh
单位: University of Toronto, University of Singapore
出版: Neural Computation, 2006
Logistic belief net
Logistic belief nets (Neal, 1992)由随机二值单元组成。这种网络被用于生成数据时,激活单元i的概率是它直接祖先j的状态的logistic函数:
其中 bi 是单元i的偏置值。
相消解释(explaining away)
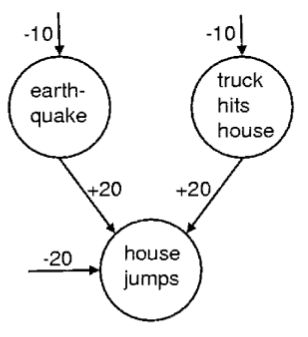
这里是一个logistic信念网络的例子,描述了这样一个场景:如果我们观察到到房子倒塌(?),那么可能有两个高度负相关的,独立的,出现概率很小的原因。凭空伸出来指向结点的是该单元的偏置值,例如earthquake的偏置值为-10,表示这一单元关闭的可能性比开启大 e10 倍,由earthquake和truck hits house指向house jumps的两个箭头代表权重w。由上面的公式可知,如果地震结点开启,卡车结点关闭,那么jump结点的总输入为0,得到的jump的概率为1/2,也就是说房子有一半机会倒,一半机会不倒(真是无力吐槽这个例子了)。然而将两个结点都激活来解释jump现象是没有意义的,因为两者同时发生的概率是 e−20 。当地震结点激活时,它”explain away”了卡车结点。
complementary priors
explaining away现象使得有向信念网络的推断变得困难。在稠密网络中,潜变量的后验分布在大部分情况下都是很难处理的。马尔可夫链式蒙特卡罗方法可以做到从后验分布中采样,然而这种方法时间开销很大。很多方法尝试用比较简单的分布来近似真正的后验分布,然而如果能够找到一种方法来消除explaining away会更好。
如果一个logistic信念网络只有一个隐藏层,那么潜变量的先验分布就能够表示成连乘形式,因为在生成数据时,它们的二值状态是独立选择的。而后验分布的非独立性是由数据的似然项决定的。或者我们可以利用其他的隐藏层创建一个与第一个隐藏层似然项中分布有完全对立的相关性的“互补”先验。然后当似然项与先验概率相乘时,我们就能够得到一个能完全分解的后验分布。下图是一个简单的例子:
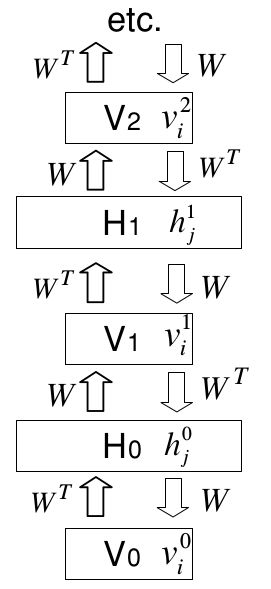
转置权重的无限有向logistic信念网络
我们可以从上图的无限有向网络中生成数据,这一过程以对一个无限深度的隐藏层的随机配置开始,然后进行一个自顶向下的传递,其中每层的每个变量的二值状态都是从上面一层被激活的输入的伯努利分布中抽取的。从这一方面来说,这个网络就与其他任何的有向无环网络一样。而与其他有向网络不同的是,我们可以通过所有隐藏层的真实后验分布来采样,通过从可视层的数据向量开始,然后利用转置权重矩阵来轮流推断每层的可分解的分布。在每个隐藏层,我们在计算后验分布前从可分解的后验分布中采样。
既然我们可以从真实的后验分布中采样,我们就可以计算数据的对数概率的导数。让我们从计算从可视层 V0 的i单元到隐藏层 H0 的单元j的生成权重 W00ij 的导数开始。一个单独向量 v0 的最大似然为:
其中< ⋅ >表示被采样的状态的均值, v̂ 0i 表示单元i如果从被采样的隐藏状态中随机重构,它被激活的概率。从第一个隐藏层的采样二值状态计算第二个隐藏层 V1 的后验分布的过程完全一样,因此 v1i 是一个以概率 v̂ 0i 从伯努利随机变量中采样的样本。因此学习规则又可写成:
因权重是重复的,整个权重的导数是所有层权重导数的和:
受限玻尔兹曼机和对比散度
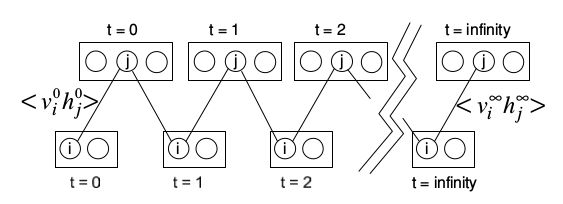
上图中的无限有向网络就是一个受限玻尔兹曼机(restricted Boltzmann machine, RBM),这或许并不明显。一个RBM有一个单层的隐藏单元层,层中单元之间并不互相连接,而与可视层有无向的对称的连接。为从RBM中生成数据,我们从两个层之一的随机状态开始进行Gibbs采样。给出一层中的当前状态,另一层中所有单元被并行地更新,这个过程不断重复,直到系统从它的平衡分布中采样,这一过程与上图中的无限网络完全相同。为学习RBM的最大似然,我们可以利用两个相关性。对于隐藏层之间的每个权重 wij ,当一个数据向量在可视层被抓住(clamped),并且隐藏层从它们的条件概率采样的时候,我们度量 <v0ih0j> 。然后利用交替Gibbs采样,我们运行下图所示的马尔可夫链,直到达到平稳分布,然后评估 <v∞ih∞j> 。训练数据的对数概率就是:
学习规则与转置权重的无限logistic信念网络相同,Gibbs采样的每一步在一个无限logistic信念网络计算精确的后验分布。
对变换表示的贪心算法
我们的算法背后的思想是让序列中每个模型收到数据的不同表示。模型对输入向量进行了一个非线性的转换,并且将其作为序列中下一个模型的输入向量。
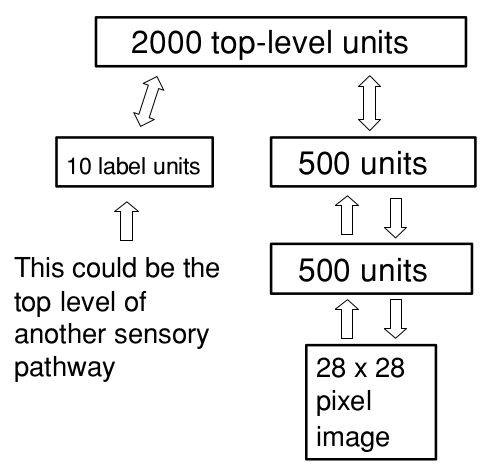
下图是一个多层的生成模型,其中最上方的两层通过无向连接进行交互,而其他连接都是有向的。每层内没有连接,并且为简化分析,所有层的结点数相同。
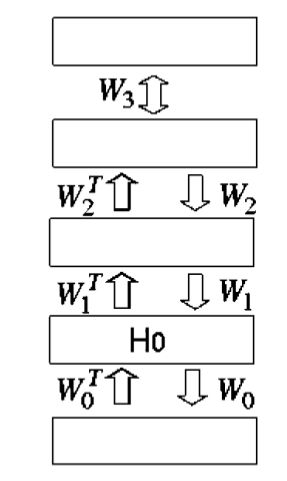
如果RBM对原数据来说是完美的模型,那么高层的数据就会被高层的权重矩阵完美地模拟。然而RBM可能并不能完美拟合原始数据,我们可以利用如下的贪心算法来使生成模型更完美:
1. 假设所有的权重矩阵都互为转置,学习 W0 。
2. 固定 W0 ,利用 WT0 来对第一个隐藏层的变量状态的可分解的近似后验分布进行推断,即使高层的权重改变意味着这种推断方法并不正确。
3. 让所有高层的权重矩阵互为转置而脱离与 W0 的转置,利用高层的数据学习一个RBM模型。
如果这种贪心算法对高层的权重矩阵作出了改变,那么一定是改进了生成模型。
利用up-down算法的微调(back-fitting)
一次学习一层的权重矩阵是有效的,但不是最优的。高层的权重一旦得到,那么无论是低层的权重还是简单的推断过程都不是最优了。贪心算法提供的次优解对于boosting等监督学习是无害的。它们的标签通常较少,并且每个标签对参数的限制不多,因此比起欠拟合,过拟合是更需要考虑的问题,回过头调整模型也就弊大于利。而无监督学习可能有很大的未标注数据集,并且每个样本的维度可能都很高,也就对生成模型造成了很大的限制。欠拟合变成了一个严重的问题,一般采取调整先习得的权重来更好适应后习得的权重来解决。
在利用贪心算法得到每层权重的初始值后,我们将用于预测的“识别”权重从用于定义模型的“生成”权重中分开,但是保留了每层的后验分布必须用一个可分解的后验分布来近似的要求,并且给出上一层的变量值后,层内的变量是条件独立的。一种“醒眠(wake-sleep)”算法的变体能够允许高层的权重影响低层的权重。在“向上”过程中,识别权重在自底向上的过程中使用,用来为每个隐藏变量随机选择一个状态。而有向连接的生成权重随即被利用极大似然方法进行调整。而顶层的无向连接是通过调整RBM来适应倒数第二层的后验分布来习得的。
向下的传递从顶层的联合单元开始,利用自顶向下生成连接来随机激活下层的单元。在向下传递的过程中,顶层非定向的连接和生成的定向连接并未改变。只有自底向上的识别权重改变了。这与醒-眠算法中sleep的阶段是相等的,如果联想单元能够在初始化向下传递过程前收敛到它的平衡分布。然而如果联想单元是用向上传递过程初始化,并且在初始化向下传递过程之前只允许有限次数的交替Gibbs采样,那么这是一种“对比”的醒眠算法。
MNIST数据集实验
训练阶段
实验利用了MNIST数据集来对网络进行评估。下图是由44000张训练图片进行训练的,训练集被平均分为了440个mini-batch,每个mini-batch包含每个类的10个样本。
在训练的初始阶段用贪心算法分别训练每层的权重,从最底层开始。每一层在整个训练集上训练了30次(称为epoch)。在训练过程中,每个RBM的可见单元都取0或1的实值。在训练最低层时这个实值是归一化的像素亮度。在训练高层的权重时,可见单元是实值的低层单元的激活值。在训练RBM时,每个RBM的隐藏层都使用了随机的二值。贪心算法在3G Xeon处理器上MATLAB需要运行数小时,运行结束后error rate能达到2.49%。
在训练顶层的权重时(联想单元),可以将标签被作为一部分输入。标签被表示为由10个单元组成的”softmax”组的某一单元的激活。当这一组内的单元被之前的几层重构后,只有一个单元会被激活,第i个单元被激活的概率为:
其中 xi 是单元i接受到的总输入。神奇的是深度网络内部的学习规则并没有受到softmax组竞争的影响。竞争影响着一个单元的激活概率,并且只影响softmax组的激活函数。
在一层接一层的贪心训练之后,就开始利用不同的学习率和不同的权重衰减,用up-down算法来对300次epoch进行训练。学习率,动量,权重衰减通过多次训练并观察性能来选择。
在验证集上表现最好的网络被用来对测试集进行测试,得到了1.39%的error rate。再利用整个60000张图片的训练集进行训练,最终得到的error rate为1.25%。