《Pruning Filters for Efficient Convnets》论文笔记
1. 概述
CNN网络经被在众多方面展现了其成功,但是随之而来的是巨大的计算量与参数存储空间。这篇论文中给出一种剪除卷积滤波器的方法(确实会影响精度),但是移除这些滤波器与其对应的feature map之后确实带来计算量的降低,而且并不会导致连接的稀疏,从而就并不需要支持稀疏的卷积库,可以使用现有的BLAS库。在实验中减少了VGG-16中34%和ResNet-110中38%的计算量,并且通过重新训练获得了与原网络近似的精度。
然而,单纯剪裁参数量并不是减少计算时间的必要条件(分类网络),因为分类网络诸如VGG-16中90%的参数是在全连接层,但是却只有1%不到的浮点运算。实际上卷积层也是能被压缩和加速的,但是需要稀疏的BLAS库,甚至特定的硬件。参数总量可以使用average pooling减少,卷积层的运算量可以通过在网络初始阶段下采样来减小,然而,网络越来越深,卷积层中的计算量占据了计算量的主要部分。
那么通过移除卷积中多余的滤波器也能够加速网络,这是一种naturally structured way。这样的方法实现重新训练,此外这里使用one-hot的键值重新练策略而不是layer-wise的方法,这样可以加速重新训练的时间。
2. Channel Pruning
2.1 单个layer的pruning
这里使用 n i n_i ni表示第 i i i个卷积层的输入通道数, ( h i , w i ) (h_i,w_i) (hi,wi)是输入feature map的宽高。当前卷积层将输入feature map(维度 x i ∈ R n i ∗ h i ∗ w i x_i \in R^{n_i*h_i*w_i} xi∈Rni∗hi∗wi)转换到feature map输出 x i + 1 x_{i+1} xi+1(维度 x i + 1 ∈ R n i + 1 ∗ h i + 1 ∗ w i + 1 x_{i+1} \in R^{n_{i+1}*h_{i+1}*w_{i+1}} xi+1∈Rni+1∗hi+1∗wi+1)。这样的操作是通过使用3D的滤波器 F i , j ∈ R n i ∗ k ∗ k F_{i,j} \in R^{n_i*k*k} Fi,j∈Rni∗k∗k在feature map上做运算得到的,这里是一个滤波器,那么总的滤波器就可以表示为 F i ∈ R n i ∗ n i + 1 k ∗ k F_i \in R^{n_i*n_{i+1}k*k} Fi∈Rni∗ni+1k∗k,那么总的计算量就是 n i + 1 n i k 2 h i + 1 w i + 1 n_{i+1}n_ik^2h_{i+1}w_{i+1} ni+1nik2hi+1wi+1。那么剪除掉多余的滤波器并不只是当前层的计算量减少,与之相关的后序特feature map也是会消失的,见下图
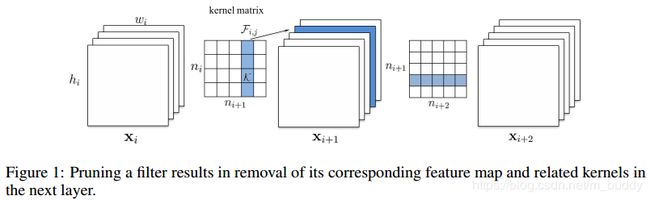
论文中的方法在训练好的模型上剪除不太重要的滤波器,并且使得精度的下降最小。这里使用滤波器中参数的绝对值和 ∑ ∣ F i , j ∣ \sum |F_{i,j}| ∑∣Fi,j∣(L1范数)作为剪裁的度量标准,该标准反映了对应输出feature map的重要程度,图2中的a图反映了滤波器参数的绝对值在VGG-16中各层的分布情况。论文中发现剪裁最小的滤波器其效果比剪裁随机或是更大滤波器的效果好;与基于激活的特征图裁剪相比,我们发现“L1-norm”是一个很好的数据自由筛选标准。
在第 i i i个卷积层中剪裁掉 m m m个滤波器的步骤描述如下:
1)对于每个滤波器 F i , j F_{i,j} Fi,j计算它们的卷积核参数的绝对值和 s j = ∑ l = 1 n i ∑ ∣ K l ∣ s_j=\sum_{l=1}^{n_i}\sum |K_l| sj=∑l=1ni∑∣Kl∣;
2)对 s j s_j sj按照从小到大排序;
3)去掉前面 m m m个滤波器,那么这 m m m个滤波器和其生成的feature map也会被剪除;
4)再将剩下的滤波器参数存储到新的模型当中。
与权重剪枝(pruning weights)的关系:滤波器剪枝和权重剪枝是类似的。但是权重剪枝的阈值需要精细设计,并且很难预测剪枝过后滤波器的个数。此外,这会导致卷积核的稀疏,这会因为缺少有效地稀疏计算库而变得困难。
与滤波器上group-sparse正则化的关系:在卷积滤波器上使用group-sparse正则化( ∑ j = 1 n i ∣ ∣ F i , j ∣ ∣ 2 \sum_{j=1}^{n_i}||F_{i,j}||_2 ∑j=1ni∣∣Fi,j∣∣2),会导致权重趋近于0。在实际中并没有发现L1与L2的在滤波器选择上的显著区别,滤波器中权重大的自然也就是重要的。对于L1与L2作为剪枝的依据在论文中做了论述,得到的实验结果如下:

从中得到的结果就是两个差的并不是很大,在它给出的结果里面L1还好于L2。
2.2 多个layer的pruning
在实验中对VGG-16中涉及到的层进行剪枝得到他们对于剪枝自后对准确率的影响。为了避免引入层之间的中间参数,使用相同的裁剪比例。对于一些对剪裁比较敏感的层,使用更小的剪裁比例设置不剪裁。
在CNN网络中进行逐层剪枝是相当耗时的,理解怎么实现多层上进行滤波器剪裁是很有必要的。1)在整个网络中进行剪裁使得拥有网络鲁棒性的全局视角,进而可以得到更小的网络。2)对于复杂的网络,全局的方法是相当必要的。例如,ResNet,剪裁残差快的feature map会导致对其它层额外地剪裁。对于多层剪裁,可以从以下两个层间滤波器选择策略:
1)单独剪裁(Independent pruning)以确定哪些滤波器应该被剪裁,图中在剪除右边的滤波器的时候要考虑黄色的值,相当于两组滤波器相互独立。
2)贪婪剪枝(Greedy pruning)需要考虑在前一层中已经删除的过滤器,也就是图中黄色的方块区域。
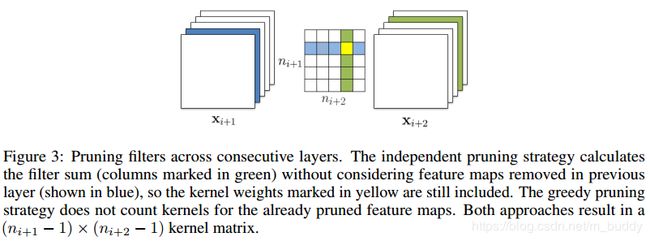
论文指出greedy的方法在多个滤波器组剪裁的时候效果更好。该策略在计算绝对权值和时不考虑前面修剪过的特征映射的核。
2.3 多分枝结构的pruning
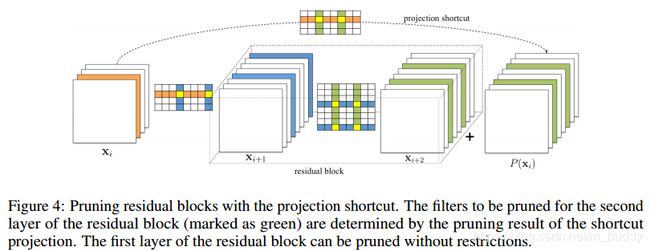
对于复杂网络结构,比如残差网络的处理。这里处理滤波器组就不能像在之前的网络一样了,它的结构就要求必须仔细地进行处理。首先,残差块的第一个卷积是可以被任意剪裁的,因为并不会影响最后的输出feature map数量;残差块的第二卷积与之前映射过来的feature map是一一对应的,这就使得比较难以剪裁;但是由于对应过来的feature map重要性是强于残差网络的输出的,所以剪裁应该由前者决定。
2.4 剪裁网络的康复训练
使修剪之后的网络获得原有的精度主要由两种策略可选:
1)剪裁一次之后重新练,剪裁多层的滤波器,之后重新训练达到原始网络的精度。
2)剪裁和重新练交替进行,逐层或是逐滤波器剪裁然后重新练,在进行下一层剪裁的时候需要完成重新练,让网络去适应这个改变。
这两种方法都是只进行一次剪裁与重新练(layer by layer),因而整个剪裁的周期很短。但是,要是剪裁的比例过大或者剪裁了一些比较敏感的层那就gg了。第二种方式就是需要花太多时间去迭代了-_-||。显然第二种的要好一些,第一种未免太过于暴力,造成无法挽救的剪裁。
3. 实验
3.1 剪裁实验
先给一个总的剪裁结果总表吧,如下图所示:
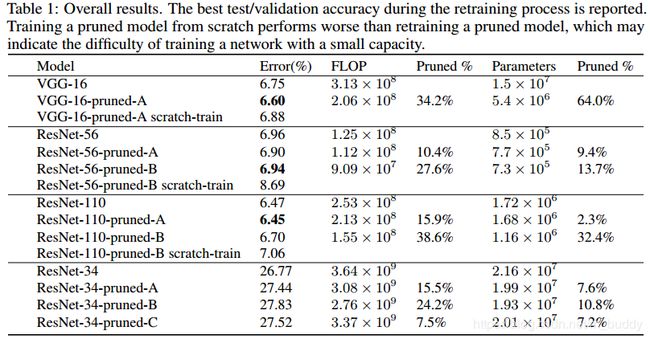
对于VGG这种类型的网络没什么好说的,重点是那种多分支的网络结构,操作起来就比较困难了。作者先后尝试了不修剪残差块的输出,只修剪残差块中的第一个卷积(因为可以随便整),但是要操作后面的时候就出问题了,可以从下面的两幅图中看出,剪裁就变得很敏感,不好搞了。
首先,剪裁残差块的第一个卷积得到的实验结果:
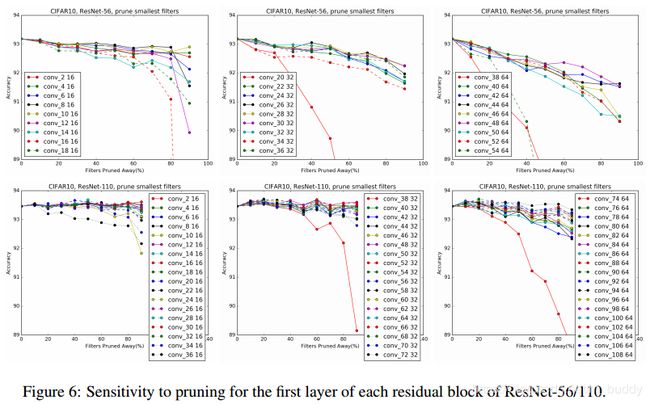
接下来就是剪裁第二个了
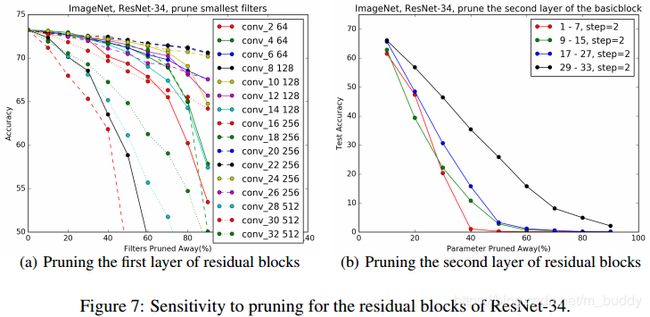
就可以看到这个东西就不是很好操作了。
3.2 剪裁策略
滤波器删除规则的实验,从实验结果中可以看出删除小的滤波器策略,随机删除策略,最大滤波器删除策略,它们的结果是依次递减的。也就是说明了文章提出剪裁依据有效(这里并没有说最佳哟,而且它也没提出来呀)。

除此之外,还尝试了使用其它的剪裁策略

4. 个人总结
在这篇论文中具体给出了CNN网络剪裁的方法,但是网络剪裁本来就是一个矛盾的问题,一方面需要裁剪网络的大小,一方面需要保持原有网络的表达能力。使用channel权重排序进行channel pruning的方式有其实际依据,但是pruning本来就是一个组合优化问题,单纯使用排序取top k的方式也有它的局限性,但是至少没有太差。后面学者使用最优化方法去解决该问题的,效果还不错。