深度学习总结（lecture 7）Network in Network（NIN）

lecture 7：Network in Network（NIN）

目录

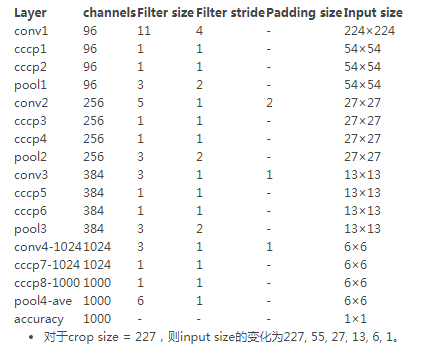
1、NIN结构

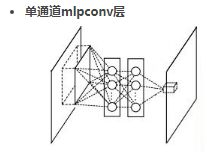
2、MLP卷积层

• 传统CNN的局部感受野窗口的运算，可以理解为一个单层的网络。
• MLPconv层是每个卷积的局部感受野中还包含了一个微型的多层网络。
• MLPconv采用多层网络结构（一般3层）提高非线性，对每个局部感受野进行更加复杂的运算。

3、全局均值池化

4、总体网络架构

1000物体分类：4层NIN+全局均值池化

5、NIN补充

5.1广义线性模型（GLM）的局限性

• 经典CNN中的卷积层就是用线性滤波器对图像进行内积运算，在每个局部输出后面跟着一个非线性的激活函数，最终得到的叫作特征图。
• 这种卷积滤波器是一种广义线性模型。所以用CNN进行特征提取时，其实就隐含地假设了特征是线性可分的，可实际问题往往不是线性可分的。
• GLM的抽象能力比较弱，比线性模型更有表达能力的非线性函数近似器（比如MLP,径向基神经）

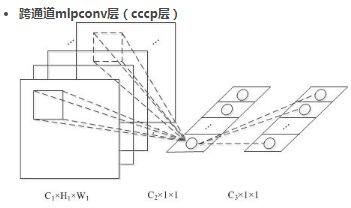
5.2CCCP层

MLPconv=CONV + MLP，因为conv是线性的，mlp是非线性的，mlp能够得到更高的抽象，泛化能力更强。

跨通道时，mlpconv=卷积层 + 1×1卷积层，此时mlpconv层也叫cccp层

6、1*1卷积的作用

7、手势识别RGB图像——NIN结构

收敛缓慢，且震荡
加了一层softmax ，第一三块后加了BatchNormalization，基本解决了

def NIN(input_shape=(64,64,3), classes=6):

    X_input = Input(input_shape)

    "block 1"
    X = Conv2D(filters=4, kernel_size=(5,5), strides=(1,1), padding='valid', activation='relu', name='conv1')(X_input)
    X = BatchNormalization(axis=3)(X)
    X = Conv2D(filters=4, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp1')(X)
    X = Conv2D(filters=4, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp2')(X)
    X = MaxPooling2D((2,2), strides=(2,2), name='maxpool1')(X)

    "block 2"
    X = Conv2D(filters=8, kernel_size=(3,3), strides=(1,1), padding='valid', activation='relu', name='conv2')(X)
    X = BatchNormalization(axis=3)(X)
    X = Conv2D(filters=8, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp3')(X)
    X = Conv2D(filters=8, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp4')(X)
    X = AveragePooling2D((2,2), strides=(2,2), name='maxpool2')(X)

    "block 3"
    X = Conv2D(filters=16, kernel_size=(3,3), strides=(1,1), padding='valid', activation='relu', name='conv3')(X)
    X = BatchNormalization(axis=3)(X)
    X = Conv2D(filters=16, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp5')(X)
    X = Conv2D(filters=16, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp6')(X)
    X = MaxPooling2D((2,2), strides=(2,2), name='maxpool3')(X)

    "block 4"
    X = Conv2D(filters=6, kernel_size=(3,3), strides=(1,1), padding='same',  activation='relu', name='conv4')(X)
    X = BatchNormalization(axis=3)(X)
    X = Conv2D(filters=6, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp7')(X)
    X = Conv2D(filters=6, kernel_size=(1,1), strides=(1,1), padding='valid', activation='relu', name='cccp8')(X)
    X = AveragePooling2D((6,6), strides=(1,1), name='Avepool1')(X)

    "flatten"
    X = Flatten()(X)
    X = Dense(classes, activation='softmax', name='fc1')(X)

    model = Model(inputs=X_input, outputs=X, name='NIN')

    return model