【第三周深度学习总结】
第三周深度学习总结
论文学习
ResNet
重要结构
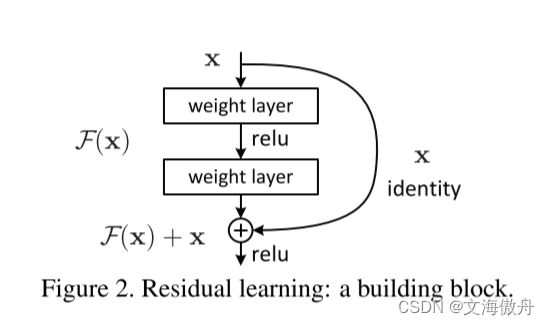
结构创新点
通过在block中加入identity map,假设之前想要学习的映射为 H ( x ) H(x) H(x),那么现在可以知道 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x,则现在网络底层学习的映射变为了 H ( x ) − x H(x)-x H(x)−x,这个部分的学习较之前更为容易。同时由于添加了short cut结构,使得整个网络在反向梯度传播的过程中梯度不至于过小为0,保证了不易出现梯度消失的问题,从而使网络深度大幅增加,使网络可以学习的特征能力大幅增强。
网络结构

ResNeXt
重要结构
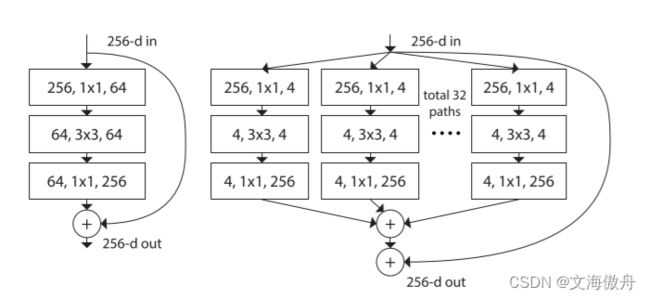
创新点
对原论文block结构进行替换,通过添加分组卷积的方法可以较少计算量
对于一般输入inchannel,输出outchannel , k e r n e l s i z e = n kernelsize=n kernelsize=n,可以知道参数量为
i n c h a n n e l ∗ n ∗ n ∗ o u t c h a n n e l inchannel*n*n*outchannel inchannel∗n∗n∗outchannel,而如果使用g的分组卷积,可以知道参数量为
n ∗ n ∗ i n c h a n n e l / g ∗ o u t c h a n n e l / g ∗ g = n ∗ n ∗ i n c h a n n e l ∗ o u t c h a n n e l / g n*n*{inchannel}/{g}*{outchannel}/{g}*g=n*n*inchannel*outchannel/g n∗n∗inchannel/g∗outchannel/g∗g=n∗n∗inchannel∗outchannel/g,参数量减少 1 / g 1/g 1/g
对于以上结构的等价,用分组卷积去替代原ResNet中的普通卷积,在输入输出维度相同的情况下可以有效减少参数量。
网络结构

猫狗大战代码
代码结构相同部分分析
数据导入
在实验开始时尝试导入完全的AI研习社数据,结果导致colab任务中断,于是开始使用老师整理的训练集,但在测试集上仍然使用了AI研习社的数据。
使用Dataset和DataLoader相关类去自定义导入,自定义类由torch.utils.data.Dataset继承而来,主要自定义__init__,__len__,__getitem__ 三个函数。首先需要得到所有图片集合的trainpath和testpath
trainDogfile='dogscats/train/dogs'
trainCatfile='dogscats/train/cats'
testfile='dogscats/test'
trainDogpath=[os.path.join(trainDogfile, x) for x in os.listdir(trainDogfile)]
trainCatpath=[os.path.join(trainCatfile, x) for x in os.listdir(trainCatfile)]
testpath=[os.path.join(testfile, x) for x in natsorted(os.listdir(testfile),alg=ns.IC)]
trainpath=trainDogpath+trainCatpath
这里涉及的操作都是字符串操作
由于这里训练集并没有标号,我们需要手动标号
df_labels={
'cat': 0,
'dog': 1
}
class_names=['cat', 'dog']
num_class=len(class_names)
之后会在__getitem__ 中对每一张图片进行标号
class ImageDataset(torch.utils.data.Dataset):
def __init__(self, df_labels, paths, kind='train', transform=None):
super().__init__()
self.df_labels=df_labels
self.paths=paths
self.transform=transform
self.kind=kind
def __len__(self):
return len(self.paths)
def __getitem__(self, index):
image_path=self.paths[index]
image=PIL.Image.open(image_path)
if self.transform is not None:
image=self.transform(image)
if self.kind=='train':
if trainpath[index].split('/')[-2]=='cats':
label=df_labels['cat']
else:
label=self.df_labels['dog']
return (image, label)
else:
return image
这里对训练集和测试集做了不同区分,训练集进行了标号,而测试集没有标号
图片处理采用了最基本的变化
transformations = torchvision.transforms.Compose(
[ torchvision.transforms.Resize((256, 256)),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
]
)
注意如果是resnet18则将图片resize(224,224)
最后使用torch.utils.data.DataLOader 对数据集进行加载操作
trainSet=ImageDataset(df_labels,trainpath,'train',transformations)
testSet=ImageDataset(df_labels,testpath,'test',transformations)
trainLoader=torch.utils.data.DataLoader(trainSet,batch_size=64,shuffle=True)
testLoader=torch.utils.data.DataLoader(testSet,batch_size=64,shuffle=False)
除了数据准备阶段,最后的测试集数据写入代码也完全相同
result=[]
logs='dogscats'
result=pandas.Series(test(model, testLoader, result))
submission=pandas.concat([pandas.Series(range(0,2000)),result], axis=1)
submission.to_csv(os.path.join(logs,'submission_ResNet/LeNet.csv'),index=False)
LeNet代码
class LeNet(torch.nn.Module):
def __init__(self, output_dim):
super().__init__()
self.conv1 = torch.nn.Conv2d(in_channels=3,
out_channels=6,
kernel_size=5)
self.conv2 = torch.nn.Conv2d(in_channels=6,
out_channels=16,
kernel_size=5)
self.fc_1 = torch.nn.Linear(16 * 61 * 61, 120)
self.fc_2 = torch.nn.Linear(120, 84)
self.fc_3 = torch.nn.Linear(84, output_dim)
def forward(self, x):
#(3, 256, 256) ---> input
x = self.conv1(x)
#(6, 252, 252) ---> output
x = torch.nn.functional.max_pool2d(x, kernel_size=2)
#(6, 126, 126)
x = torch.nn.functional.relu(x)
x = self.conv2(x)
#(16, 122, 122)
x = torch.nn.functional.max_pool2d(x, kernel_size=2)
#(16, 61, 61)
x = torch.nn.functional.relu(x)
x = x.view(x.shape[0], -1)
x = self.fc_1(x)
x = torch.nn.functional.relu(x)
x = self.fc_2(x)
x = torch.nn.functional.relu(x)
x = self.fc_3(x)
return x
在常规训练后,使用上面提到的测试代码将测试结果写入csv文件,提交最终结果为64.55
ResNet代码
准确率
![]()
网络结构
这里直接使用torchvision.models.resnet18 进行训练,代码如下
#model=LeNet(2).to(device)
weights = torchvision.models.ResNet18_Weights.DEFAULT
model=torchvision.models.resnet18(weights=weights)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
model.fc=torch.nn.Linear(model.fc.in_features,2)
这里需要将最终全连接层修改为我们想要的维度–2,之后进行正常训练和测试写入即可。最后得到的结果为86.8.
思考题
-
Residual Learning

通过在block中加入identity map,假设之前想要学习的映射为 H ( x ) H(x) H(x),那么现在可以知道 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x,则现在网络底层学习的映射变为了 H ( x ) − x H(x)-x H(x)−x,这个部分的学习较之前更为容易。同时由于添加了short cut结构,使得整个网络在反向梯度传播的过程中梯度不至于过小为0,保证了不易出现梯度消失的问题,从而使网络深度大幅增加,使网络可以学习的特征能力大幅增强。 -
Batch Normailization原理
在实际操作中,我们会在激活函数前使用Batch Normalization,对于网络中的隐层,假设我们由 z [ i ] z^{[i]} z[i]到 z [ m ] z^{[m]} z[m],具体操作如下:
μ = 1 m ∑ i z [ i ] σ = 1 m ∑ i ( z [ i ] − μ ) z n o r m [ i ] = z [ i ] − μ σ 2 + ϵ \mu=\frac{1}{m}\sum_{i}z^{[i]} \\ \sigma=\frac{1}{m}\sum_{i}(z^{[i]}-\mu) \\ z_{norm}^{[i]}=\frac{z^{[i]}-\mu}{\sqrt{\sigma^2+\epsilon}} μ=m1i∑z[i]σ=m1i∑(z[i]−μ)znorm[i]=σ2+ϵz[i]−μ
这里 ϵ \epsilon ϵ加在分母上保证分母不为0,经过以上操作使所有数据变为均值为0、方差为1的高斯分布。但在实际中数据并不一定符合高斯分布,故
z [ i ] = γ z n o r m [ i ] + β z^{[i]}=\gamma z_{norm}^{[i]}+\beta z[i]=γznorm[i]+β
这里 γ \gamma γ和 β \beta β都是可供学习的参数。 -
为什么分组卷积可以提升准确率?既然分组卷积可以提升准确率,同时还能降低计算量,分组数量尽量多不行吗?
传统卷积中每一个 k e r n e l kernel kernel都和输入的通道数进行卷积计算,这其中有些计算冗余;同时如果每个输出与输入的一部分特征图相关联,则分组卷积可以取得更好的效果,同时采用分组卷积可以较少每片GPU压力,参考AlexNet的涉及。
但如果将分组卷积推到极致,即分组数等于通道数且等于输出通道数,即 g = C i n = C o u t g=C_{in}=C_{out} g=Cin=Cout,此时称为深度可分离卷积(Depthwise Convolution),此时卷积计算缺乏输入通道之间的信息交换,故在实际操作中想要想要灵活调整。