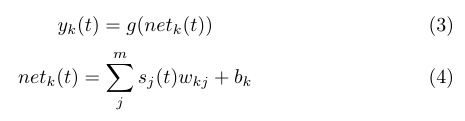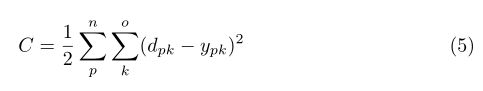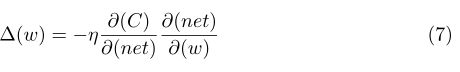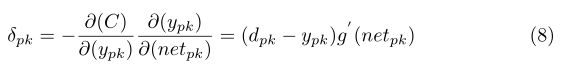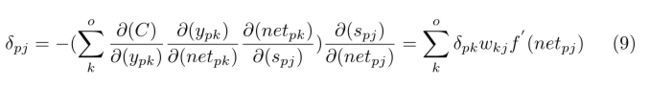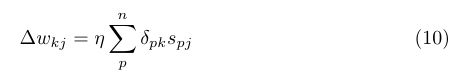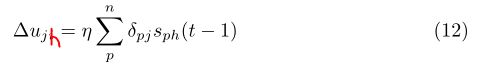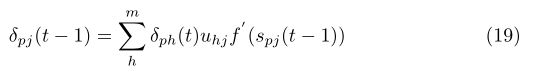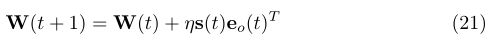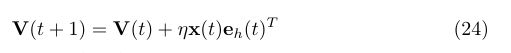深度学习 --- 循环神经网络RNN详解(BPTT)
今天开始深度学习的最后一个重量级的神经网络即RNN,这个网络在自然语言处理中用处很大,因此需要掌握它,同时本人打算在深度学习总结完成以后就开始自然语言处理的总结,至于强化学习呢,目前不打算总结了,因为我需要实战已经总结完成的算法,尤其是深度学习和自然语言的处理的实战,所以大方向就这样计划。下面讲讲本节的内容,本节的的内容和以前一样,从最初开始,慢慢探索到LSTM,废话不多说下面开始:
RNN(Recurrent Neural Network),Jordan,Pineda.Williams,Elman等于上世纪80年代末末出的一种神经网络结构模型。这种网络的本质特征是在处理单元之间既有内部的反馈连接又有前馈连接。从系统观点看,它是一个反馈动力系统,在计算过程中体现过程动态特性,比前馈神经网络具有更强的动态行为和计算能力。循环神经网络现已成为国际上神经网络丏家研究的重要对象之一。
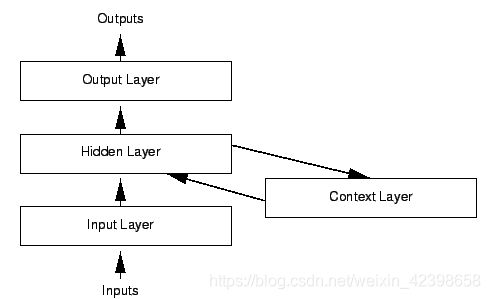
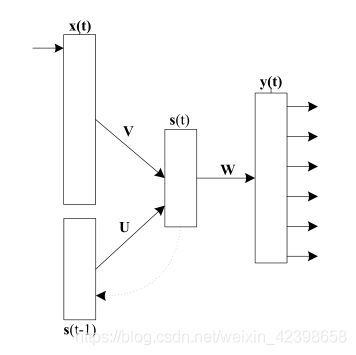
这种网络的内部状态可以展示劢态时序行为。不同于前馈神经网络的是,RNN可以利用它内部的记忆来处理任意时序的输入序列,这让它可以更容易处理如不分段的手写识别,语音识别等。在一个句子中,语意的分析和上下文很重要,因此需要考虑输入的时间序列问题,因此很自然的想法就是延时在再输入可以达到效果,下面我们看看RNN的经典结构:
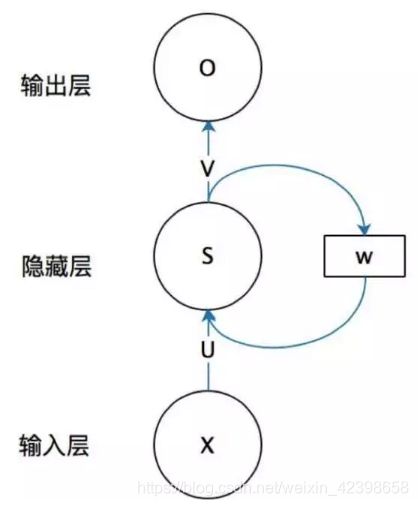
从上图我们可以看出,若果没有上下文层即Context Layer,则上面的网络就完全是一个标准的BP网络。如果加一个上文层就是循环神经网络了,加这一层的就是隐层的输出延迟一个时间单元然后和隐层输入一起再次输入到隐层进行拟合,我们看看具体的神经网络如下:
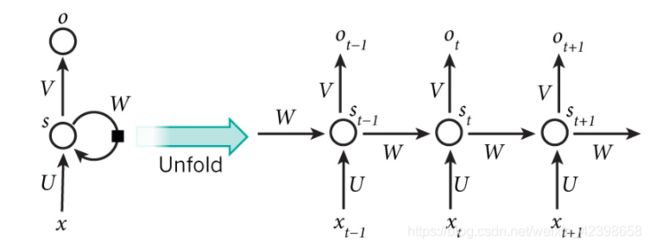
为了看清楚他们的信息流向,这里我们展开看看:
上图的左边是原始网络,右半部分为了观察时间序列的是如何参与的,我们按照时间展开即t-1,t,t + 1,这里大家需要搞明白什么意思,在BP中的中间层称为隐藏层,而在RNN里称为状态层,其中ü代表输入到隐层的权值,W代表返回的权值,V代表隐层输出到输出层的权值,我们知道BP的学习规则,而RNN是在BP的基础上进行演变而来的,因此它的学习规则也是和BP很类似,只是稍微一点变化。学习算法我们稍后介绍。下面简单介绍一下埃尔曼神经网络。
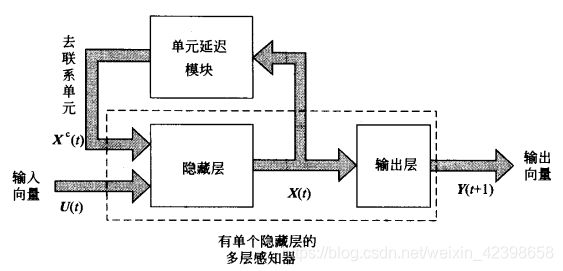
Elman神经网络:
JLElman于1990年提出一种简单的递归网络模型,如上图所示该网络输人层接受两种信号:一种是外加输人![]() ;一种是来自隐层的反馈信号
;一种是来自隐层的反馈信号![]() 。将接受反馈的节点称为联系单元(contextunit),
。将接受反馈的节点称为联系单元(contextunit),![]() 表示联系单元在时刻
表示联系单元在时刻![]() 的输出;隐层输出为
的输出;隐层输出为![]() ,为输出
,为输出![]() 当输出节点采用线性转移函数时,有如下方程:
当输出节点采用线性转移函数时,有如下方程:
隐单元: ![]()
联系单元: ![]()
输出单元: ![]()
还有一种递归神经网络NARX,也是很早就出现了,这里就不详细的介绍了,有兴趣的可以自行查阅资料,下面我们看看RNN的训练算法BPTT(BackPropagation through Time)。
BPTT(通过时间反向传播)
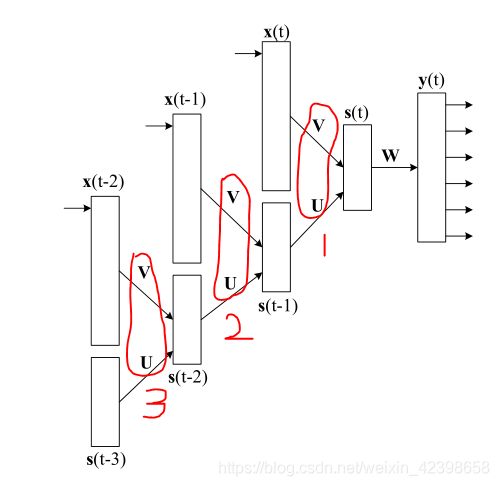
这里先上图,大家按照上面的图对比理解:
我们下面的就按照上图进行讲解训练算法,这里先说明一下符号的意义:
| 神经元层 | 描述 | 下标变量 |
|
|
输入层 前一个隐藏(状态)层 隐藏(状态)层 输出层 |
|
| 权值矩阵 | 描述 | 下标变量 |
|
|
层输入侧 一个前隐藏层 层隐藏 |
|
层输入侧![]() 隐藏层:
隐藏层:
![]() (1)
(1)
这里解释一下,(1)式是说当前隐层状态即吨时刻的状态取决于激活函数˚F和输入的![]() ,而
,而![]() 有和当前输入以及前一时刻的隐层输出(此时前一时刻还包含好多前一时刻,隐层是时间的累加和即上式的红色部分)同是加上偏置值。
有和当前输入以及前一时刻的隐层输出(此时前一时刻还包含好多前一时刻,隐层是时间的累加和即上式的红色部分)同是加上偏置值。
层隐藏![]() 输出层:
输出层:
这是输出层,同理和激活函数克以及 ![]() 决定,而
决定,而![]() 的是和隐层的多个神经元的和有关同时加上偏置值。
的是和隐层的多个神经元的和有关同时加上偏置值。
式上![]() 分别对应关系着激活函数,而
分别对应关系着激活函数,而![]() 就是待训练的权值矩阵,下面我们就看看该网络的反向传播学习算法:
就是待训练的权值矩阵,下面我们就看看该网络的反向传播学习算法:
BP
下面构建我们的代价函数这里采样误差平方和为代价函数。
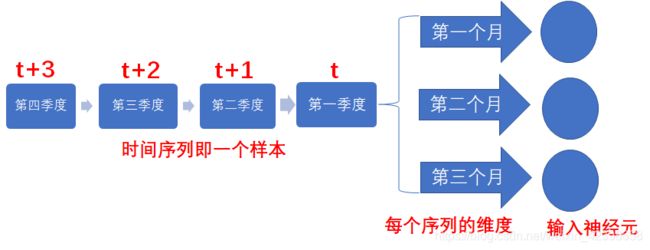
其中d是期望值,Y是网络的输出值,下标p是代表的样本个数,这里为Ñ个样本,这里大家需要理清上面的吨是时间即前一个时间单位和后一个时间单位,这里大家需要好好体会理解,还是简单解释一下,例如在自然语言处理中,我们的样本就是很多的句子,而每个样本即每个句子中又分为很多词或者特征,而我们输入神经网络里是按照一个词一个词(即一个维度)输入进去的,因此有时间序列吨的概念。这里大家需要理解一些,别晕了。搞清楚什么是样本,什么是序列,什么是维度,时刻想着这是序列的问题。为了让大家搞明白我在举个例子,例如公司的一年四个季度的收入情况,这里呢,很多公司就是很多样本,不同公司就是不同的样本,而一个公司的的四个季度的收支情况就是时间序列(第一季度第二季度等等),而每个季度有三个月组成,那么 三个月就是维度,即每个序列有三个维度,而我们输入到神经元的是每个时间序列(首先输入第一季度,然后是第二季度等等)而每个季度有3个维度即每个季度有三个月,因此对应三个神经元,下面画出图,大家结合图还好理解他们的关系:
这里大家结合刚开始的下标进行理解,我觉得理解应该没问题了,那么我们继续往下讲,下面就是我们最基本的BP了很简单,这里我把公式拿出来,简单的叙述一下:
上面是很经典的BP反向传播的计算公式,如果对此不理解或者感觉理解困难的同学说明你的基础不扎实,请好好补一下BP的算法推倒,推倒具体请查看我的这篇文章,下面就看看三个权值更新:
到这里还是我们BP的反向传播的算法,这里需要注意是以上都是针对当前时间序列也就是吨时刻,这里唯一新一点的东西就是下式的ü权值的更新就是隐层的p个样本对隐层的第j个神经元的误差乘上上一个时刻隐层的神经元的输出在乘上学习率就对U的调整了,这里大家好好理解,我感觉都不难的,把BP该清楚还是很容易的。
这就是权值更新的过程,但是该网络使用BP算法的有什么优缺点呢这里我们开看看?
我们在看看(12)式,在更新ü时,需要他一上的时刻![]() 的值上面只用到这一层,但是
的值上面只用到这一层,但是![]() 的值汉语中类似的依赖上一个
的值汉语中类似的依赖上一个 ![]() 的值等等,这样会有很多层,如上图所示,但是我们怎么更新这里的权值ù和V呢?为了解决这个问题,引入了BPTT,我们下面就详细的讲讲他是如何更新的,想要搞明白BPTT,上面的图很关键,好下面我先使用口语化和大家解释他是如何更新所有时间序列的权值的:
的值等等,这样会有很多层,如上图所示,但是我们怎么更新这里的权值ù和V呢?为了解决这个问题,引入了BPTT,我们下面就详细的讲讲他是如何更新的,想要搞明白BPTT,上面的图很关键,好下面我先使用口语化和大家解释他是如何更新所有时间序列的权值的:
这里我们先从输出得到误差信号,反向传播先更新W,更新完w ^后,误差继续向下传播,更新然后![]() 的的U,V,即上图的1标记层,然后误差继续沿着1标记反向传播到
的的U,V,即上图的1标记层,然后误差继续沿着1标记反向传播到![]() ,然后更新2位置的U,V,此时问题就来了,如果我更新这里的U,V那之前的1号位置的U,V还有效吗?因为他们1,2,3 ,,,位置的U,V都是联动的,即改变他们任何一个就会改变结果,所有我么这里要求只要改变2的U,V,那么1,3 ,,等都会以相同的进行改变,现在在2号位置。然后全部改变,误差继续反向传播到3的位置,开始改变U,V,同时其他的时序的U,V跟着相同的改变,然后继续往下传播,知道最后一层后,此时训练结束了,权值的也就固定了,这就是BPTT的精髓了即时间不停的往前追溯直到刚开始的那个时间为止每追溯一层的权值都会统一根据本次的追溯进行调节权值U,V,直到追溯到刚开始的 时间。大家好好理解,但是这里又有问题了,每次训练都需要追溯到刚开始的时间吗?通常情况是追溯到3到5层就足够了,为什么呢?因为追溯时间越多说明层数越多,那么反向误差面临的梯度消失就会出现了,越往后U,V的改变量越小,因此一般3到5层就够了下面给出BPTT的表达式:
,然后更新2位置的U,V,此时问题就来了,如果我更新这里的U,V那之前的1号位置的U,V还有效吗?因为他们1,2,3 ,,,位置的U,V都是联动的,即改变他们任何一个就会改变结果,所有我么这里要求只要改变2的U,V,那么1,3 ,,等都会以相同的进行改变,现在在2号位置。然后全部改变,误差继续反向传播到3的位置,开始改变U,V,同时其他的时序的U,V跟着相同的改变,然后继续往下传播,知道最后一层后,此时训练结束了,权值的也就固定了,这就是BPTT的精髓了即时间不停的往前追溯直到刚开始的那个时间为止每追溯一层的权值都会统一根据本次的追溯进行调节权值U,V,直到追溯到刚开始的 时间。大家好好理解,但是这里又有问题了,每次训练都需要追溯到刚开始的时间吗?通常情况是追溯到3到5层就足够了,为什么呢?因为追溯时间越多说明层数越多,那么反向误差面临的梯度消失就会出现了,越往后U,V的改变量越小,因此一般3到5层就够了下面给出BPTT的表达式:
根据第9式可推出下面的式子
下面使用矩阵的形式给出BPTT的权值调整过程;
误差信号:
输出权值调整宽:
误差从输出层传播到隐藏层:
d表示误差信号按单元计算得到。
权值V的更新:
权值ü的更新;
上面就是权值的调整的向量化,下面给出BPTT递归更新的公式:
其中![]() 的英文追溯到时间的层数,如
的英文追溯到时间的层数,如![]() 说明追溯到第三层,图产品上就是
说明追溯到第三层,图产品上就是 ![]() 的示意图。
的示意图。
确定![]() 值以后就可以递归的调用U,V的权值调用公式了:
值以后就可以递归的调用U,V的权值调用公式了:
上面应该是![]() ,大家需要注意。
,大家需要注意。
我们简单的讨论一下(26)式,他是说误差信号反向传播到上一层,然后更新ü和V,因为每次的向上传播都会更新其实就是U,V的累加,这里大家需要理解这里的累加为什么?这就是BPTT算了。
好了,本节到此结束了,下一节我们探索BPTT的优缺点,根据缺点我们引入LSTM算法解决了BPTT的缺点,下一节我们将详细讲解LSTM的工作原理。
本篇参考文献为《BackPropagation Through Time》 Jiang Guo 2013.7.20