sklearn线性回归,支持向量机SVR回归,随机森林回归,神经网络回归参数解释及示例

1.sklearn线性回归

线性回归，其中目标值 y 是输入变量 x 的线性组合。 在数学概念中，如果  是预测值。

在整个模块中，我们定义向量  作为 coef_ ，定义  作为 intercept_ ，是它的截距。

LinearRegression 拟合一个带有系数  的线性模型，使得数据集实际观测数据和预测数据（估计值）之间的残差平方和最小。其数学表达式为:

class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

fit_intercept=True, 默认存在截距 normalize=False,默认不进行标准化处理 copy_X=True，If True, X will be copied; else, it may be overwritten.

from sklearn import linear_model
reg = linear_model.LinearRegression()
a=[[1,2], [2,3], [3,4],[1,5]]
b=[6,9,12,12]
reg.fit (a, b)
w_dt=reg.coef_
re=reg.predict(([[4,4]]))
print(w_dt)
print(reg.intercept_)
print(re)

[1. 2.]
1.0000000000000018
[13.]

2.支持向量机回归SVR

C : float, optional (default=1.0)

    误差项的惩罚参数，一般取值为10的n次幂，如10的-5次幂，10的-4次幂。。。。10的0次幂，10，1000,1000，在python中可以使用pow（10，n） n=-5~inf
    C越大，相当于希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样会出现训练集测试时准确率很高，但泛化能力弱。
    C值小，对误分类的惩罚减小，容错能力增强，泛化能力较强。

kernel : string, optional (default=’rbf’)

    svc中指定的kernel类型。
    可以是： ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ 或者自己指定。 默认使用‘rbf’ 。

degree : int, optional (default=3)

    当指定kernel为 ‘poly’时，表示选择的多项式的最高次数，默认为三次多项式。
    若指定kernel不是‘poly’,则忽略，即该参数只对‘poly’有作用。

gamma : float, optional (default=’auto’)

    当kernel为‘rbf’, ‘poly’或‘sigmoid’时的kernel系数。
    如果不设置，默认为 ‘auto’ ，此时，kernel系数设置为：1/n_features

coef0 : float, optional (default=0.0)

    kernel函数的常数项。
    只有在 kernel为‘poly’或‘sigmoid’时有效，默认为0。

probability : boolean, optional (default=False)
    是否采用概率估计。
    必须在fit（）方法前使用，该方法的使用会降低运算速度，默认为False。 

shrinking : boolean, optional (default=True)

    如果能预知哪些变量对应着支持向量，则只要在这些样本上训练就够了，其他样本可不予考虑，这不影响训练结果，但降低了问题的规模并有助于迅速求解。进一步，如果能预知哪些变量在边界上(即a=C)，则这些变量可保持不动，只对其他变量进行优化，从而使问题的规模更小，训练时间大大降低。这就是Shrinking技术。

    Shrinking技术基于这样一个事实：支持向量只占训练样本的少部分，并且大多数支持向量的拉格朗日乘子等于C。

tol : float, optional (default=1e-3)

    误差项达到指定值时则停止训练，默认为1e-3，即0.001。

cache_size : float, optional

    指定内核缓存的大小，默认为200M。

class_weight : {dict, ‘balanced’}, optional

    权重设置。如果不设置，则默认所有类权重值相同。
    以字典形式传入。
    Set the parameter C of class i to class_weight[i]*C for SVC. If not given, all classes are supposed to have weight one. The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as n_samples / (n_classes * np.bincount(y))

verbose : bool, default: False

    是否启用详细输出。
    多线程时可能不会如预期的那样工作。默认为False。

max_iter : int, optional (default=-1)
    默认设置为-1，表示无穷大迭代次数。
    Hard limit on iterations within solver, or -1 for no limit.

decision_function_shape : ‘ovo’, ‘ovr’, default=’ovr’

    Whether to return a one-vs-rest (‘ovr’) decision function of shape (n_samples, n_classes) as all other classifiers, or the original one-vs-one (‘ovo’) decision function of libsvm which has shape (n_samples, n_classes * (n_classes - 1) / 2).

    Changed in version 0.19: decision_function_shape is ‘ovr’ by default.

    New in version 0.17: decision_function_shape=’ovr’ is recommended.

    Changed in version 0.17: Deprecated decision_function_shape=’ovo’ and None.

random_state : int, RandomState instance or None, optional (default=None)

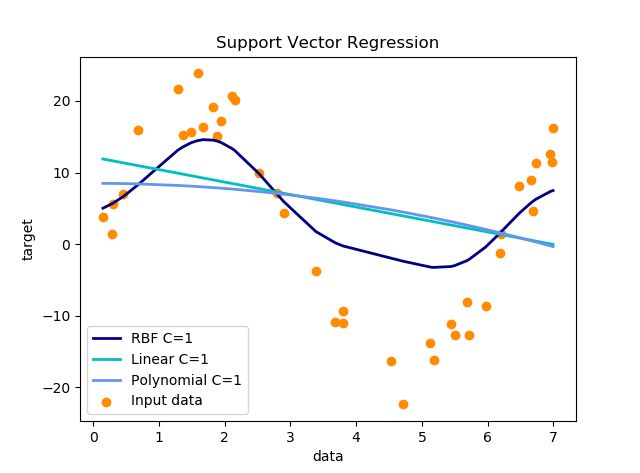
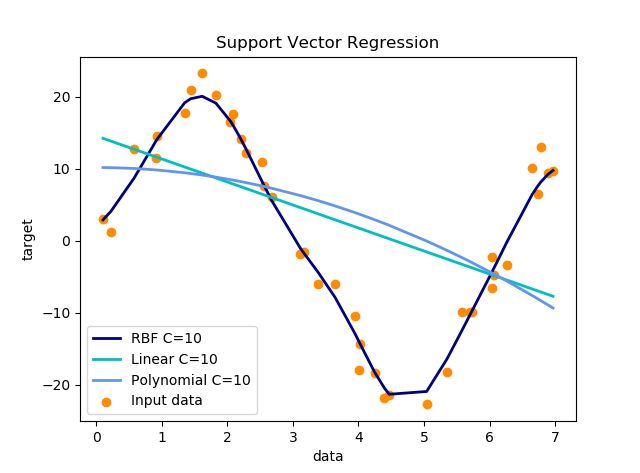
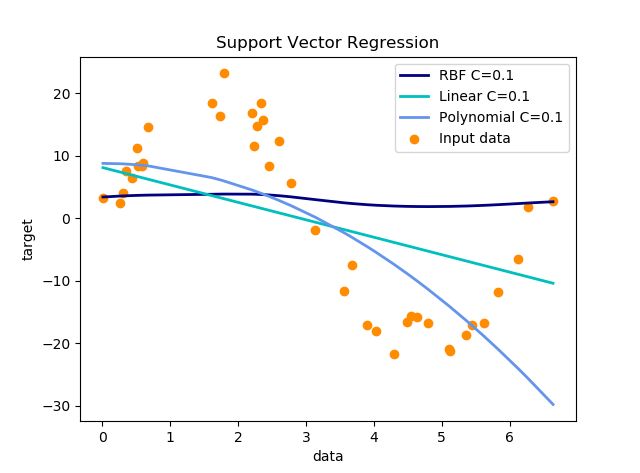
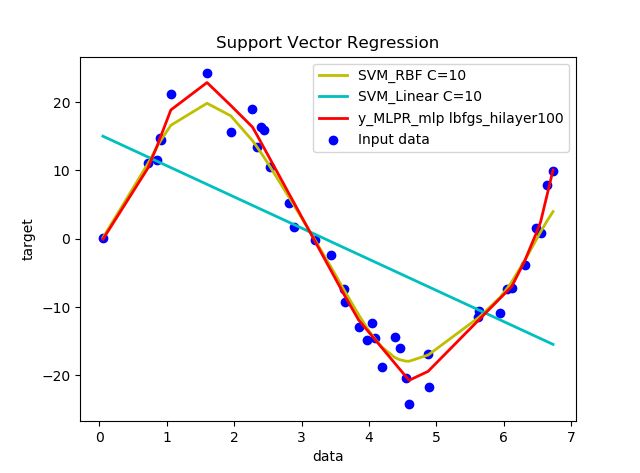
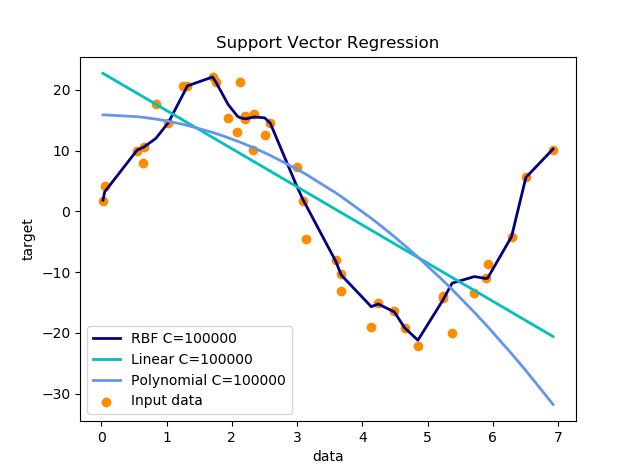
    伪随机数使用数据。 

• import numpy as np
  from sklearn.svm import SVR
  import matplotlib.pyplot as plt
  # #############################################################################
  # Generate sample data
  X = np.sort(7 * np.random.rand(40, 1), axis=0)
  y = np.sin(X).ravel()*20
  # #############################################################################
  # Add noise to targets
  noise= 9 * (0.5 - np.random.rand(40))
  y_noise=y+noise
  # #############################################################################
  # Fit regression model
  svr_rbf = SVR(kernel='rbf', C=1)
  svr_lin = SVR(kernel='linear', C=1)
  svr_poly = SVR(kernel='poly', C=1, degree=2)
  y_rbf = svr_rbf.fit(X, y_noise).predict(X)
  y_lin = svr_lin.fit(X, y_noise).predict(X)
  y_poly = svr_poly.fit(X, y_noise).predict(X)
  
  # #############################################################################
  # Look at the results
  lw = 2
  plt.scatter(X, y_noise, color='darkorange', label='Input data')
  plt.plot(X, y_rbf, color='navy', lw=lw, label='RBF C=1 ')
  plt.plot(X, y_lin, color='c', lw=lw, label='Linear C=1')
  plt.plot(X, y_poly, color='cornflowerblue', lw=lw, label='Polynomial C=1')
  plt.xlabel('data')
  plt.ylabel('target')
  plt.title('Support Vector Regression')
  plt.legend()
  plt.show()

参数设置:C取1,其他都为默认值

• 参数设置:C取10,其他都为默认值

• 参数设置:C取100,其他都为默认值

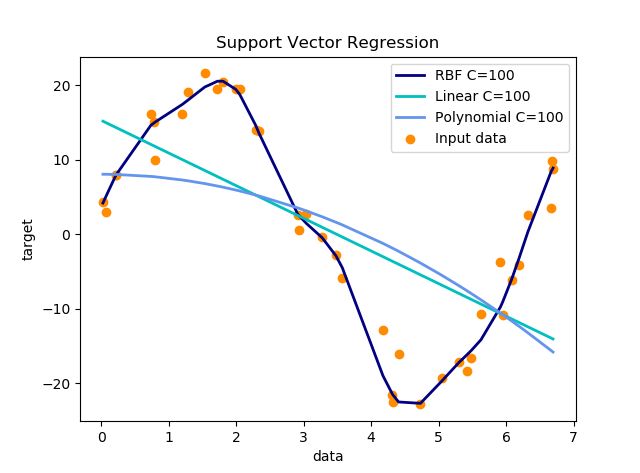
• 参数设置:C取1000,其他都为默认值

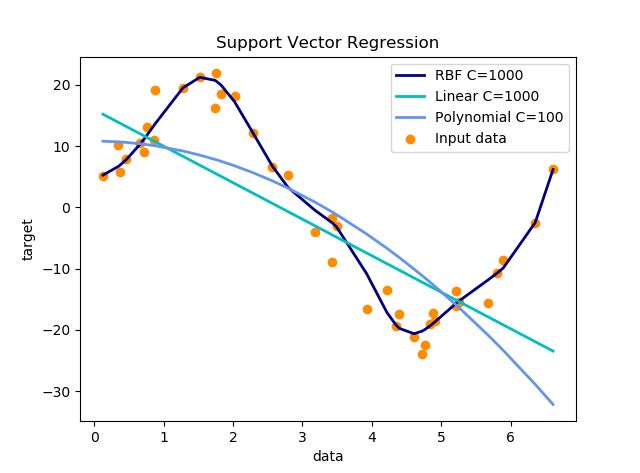
• 参数设置:C取0.1,其他都为默认值

• 参数设置:C取10000,其他都为默认值

3.随机森林回归

随机森林的生成

从样本集中通过重采样的方式产生n个样本。
假设样本特征数目为a，对n个样本选择a中的k个特征，用建立决策树的方式获得最佳分割点。

重复m次，产生m棵决策树。

多数投票机制进行预测。
随机森林中的随机是什么意思？

随机森林中的随机性主要体现在两个方面：

随机采样：随机森林在计算每棵树时，从全部训练样本（样本数为n）中选取一个可能有重复的、大小同样为n的数据集进行训练（即booststrap采样）。

特征选取的随机性：在每个节点随机选取所有特征的一个子集，用来计算最佳分割方式。

随机森林的优点：

表现性能好，与其他算法相比有着很大优势。
随机森林能处理很高维度的数据（也就是很多特征的数据），并且不用做特征选择。
在训练完之后，随机森林能给出哪些特征比较重要。
训练速度快，容易做成并行化方法(训练时，树与树之间是相互独立的)。
在训练过程中，能够检测到feature之间的影响。
对于不平衡数据集来说，随机森林可以平衡误差。当存在分类不平衡的情况时，随机森林能提供平衡数据集误差的有效方法。
如果有很大一部分的特征遗失，用RF算法仍然可以维持准确度。
随机森林算法有很强的抗干扰能力（具体体现在6,7点）。所以当数据存在大量的数据缺失，用RF也是不错的。
随机森林抗过拟合能力比较强（虽然理论上说随机森林不会产生过拟合现象，但是在现实中噪声是不能忽略的，增加树虽然能够减小过拟合，但没有办法完全消除过拟合，无论怎么增加树都不行，再说树的数目也不可能无限增加的。）
随机森林能够解决分类与回归两种类型的问题，并在这两方面都有相当好的估计表现。（虽然RF能做回归问题，但通常都用RF来解决分类问题）。
在创建随机森林时候，对generlization error(泛化误差)使用的是无偏估计模型，泛化能力强。

随机森林在Python的实现

#Import Library 
from sklearn.ensemble import RandomForestClassifier 
#use RandomForestRegressor for regression problem 
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset 

# Create Random Forest object 
model= RandomForestClassifier(n_estimators=1000) 
# Train the model using the training sets and check score 
model.fit(X, y) 
#Predict Output 
predicted= model.predict(x_test) 

随机森林在sklearn-RandomForest参数

RandomForestClassifier(
            n_estimators=10,   //树的棵数
            criterion='gini',      //分类标准
            max_depth=None,  //最大深度
             min_samples_split=2,  //最少分裂几个子节点
             min_weight_fraction_leaf=0.0,
            max_leaf_nodes=None,
             bootstrap=True, 
            n_jobs=1,    //指定并行使用的进程数
            random_state=None, 
            verbose=0,
             warm_start=False, 
             class_weight=None  //类别权重，样本不均衡时很重要
)

from sklearn.ensemble import RandomForestRegressor
import numpy as np

rf = RandomForestRegressor()


a=[[1,2], [2,3], [3,4],[1,5]]
b=np.array([[6],[9],[12],[12]])
rf.fit (a, b.ravel())
re=rf.predict([[4,4]])
print(re)
c=[[1,2], [2,3], [3,4],[1,5]]
d=np.array([[7],[11],[15],[10]])
rf.fit (c, d.ravel())
re=rf.predict([[4,4]])
print(re)

[11.4]
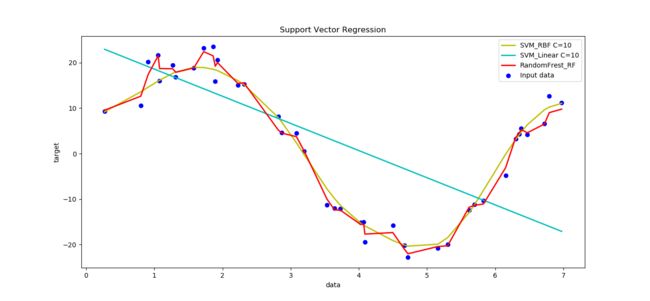
[13.7]

随机森林回归与支持向量机回归比较

import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR
import matplotlib.pyplot as plt

# #############################################################################
# Generate sample data
X = np.sort(7 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel() * 20
# #############################################################################
# Add noise to targets
noise = 9 * (0.5 - np.random.rand(40))
y_noise = y + noise
# #############################################################################
# Fit regression model
svr_rbf = SVR(kernel='rbf', C=10)
svr_lin = SVR(kernel='linear', C=10)
rf=RandomForestRegressor()
y_SVM_rbf = svr_rbf.fit(X, y_noise).predict(X)
y_SVM_lin = svr_lin.fit(X, y_noise).predict(X)
y_RF_rf = rf.fit(X, y_noise).predict(X)

# #############################################################################
# Look at the results
lw = 2
plt.scatter(X, y_noise, color='b', label='Input data')
plt.plot(X, y_SVM_rbf, color='y', lw=lw, label='SVM_RBF C=10 ')
plt.plot(X,y_SVM_lin, color='c', lw=lw, label='SVM_Linear C=10')
plt.plot(X, y_RF_rf, color='r', lw=lw, label='RandomFrest_RF')
plt.xlabel('data')
plt.ylabel('target')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

4.神经网络回归

mlp=MLPClassifier(solver=’sgd’,activation=’relu’,alpha=1e-4,hidden_layer_sizes=(50,50), random_state=1,max_iter=10,verbose=10,learning_rate_init=.1)

参数说明: 

1. hidden_layer_sizes :例如hidden_layer_sizes=(50, 50)，表示有两层隐藏层，第一层隐藏层有50个神经元，第二层也有50个神经元。 

2. activation :激活函数,{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu 
- identity：f(x) = x 
- logistic：其实就是sigmod,f(x) = 1 / (1 + exp(-x)). 
- tanh：f(x) = tanh(x). 

- relu：f(x) = max(0, x) 

3. solver： {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam，用来优化权重 
- lbfgs：quasi-Newton方法的优化器 
- sgd：随机梯度下降 
- adam： Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器 

注意：默认solver ‘adam’在相对较大的数据集上效果比较好（几千个样本或者更多），对小数据集来说，lbfgs收敛更快效果也更好。 

4. alpha :float,可选的，默认0.0001,正则化项参数 

5. batch_size : int , 可选的，默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples)，如果solver是’lbfgs’，分类器将不使用minibatch 

6. learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用，{‘constant’，’invscaling’, ‘adaptive’},默认constant 
- ‘constant’: 有’learning_rate_init’给定的恒定学习率 
- ‘incscaling’：随着时间t使用’power_t’的逆标度指数不断降低学习率learning_rate_ ，effective_learning_rate = learning_rate_init / pow(t, power_t) 

- ‘adaptive’：只要训练损耗在下降，就保持学习率为’learning_rate_init’不变，当连续两次不能降低训练损耗或验证分数停止升高至少tol时，将当前学习率除以5. 

7. power_t: double, 可选, default 0.5，只有solver=’sgd’时使用，是逆扩展学习率的指数.当learning_rate=’invscaling’，用来更新有效学习率。 

8. max_iter: int，可选，默认200，最大迭代次数。 

9. random_state:int 或RandomState，可选，默认None，随机数生成器的状态或种子。 

10. shuffle: bool，可选，默认True,只有当solver=’sgd’或者‘adam’时使用，判断是否在每次迭代时对样本进行清洗。 

11. tol：float, 可选，默认1e-4，优化的容忍度 

12. learning_rate_int:double,可选，默认0.001，初始学习率，控制更新权重的补偿，只有当solver=’sgd’ 或’adam’时使用。 

14. verbose : bool, 可选, 默认False,是否将过程打印到stdout 

15. warm_start : bool, 可选, 默认False,当设置成True，使用之前的解决方法作为初始拟合，否则释放之前的解决方法。 

16. momentum : float, 默认 0.9,动量梯度下降更新，设置的范围应该0.0-1.0. 只有solver=’sgd’时使用. 

17. nesterovs_momentum : boolean, 默认True, Whether to use Nesterov’s momentum. 只有solver=’sgd’并且momentum > 0使用. 

18. early_stopping : bool, 默认False,只有solver=’sgd’或者’adam’时有效,判断当验证效果不再改善的时候是否终止训练，当为True时，自动选出10%的训练数据用于验证并在两步连续迭代改善，低于tol时终止训练。 

19. validation_fraction : float, 可选, 默认 0.1,用作早期停止验证的预留训练数据集的比例，早0-1之间，只当early_stopping=True有用 

20. beta_1 : float, 可选, 默认0.9，只有solver=’adam’时使用，估计一阶矩向量的指数衰减速率，[0,1)之间 

21. beta_2 : float, 可选, 默认0.999,只有solver=’adam’时使用估计二阶矩向量的指数衰减速率[0,1)之间 

22. epsilon : float, 可选, 默认1e-8,只有solver=’adam’时使用数值稳定值。 

属性说明： 
- classes_:每个输出的类标签 
- loss_:损失函数计算出来的当前损失值 
- coefs_:列表中的第i个元素表示i层的权重矩阵 
- intercepts_:列表中第i个元素代表i+1层的偏差向量 
- n_iter_ ：迭代次数 
- n_layers_:层数 
- n_outputs_:输出的个数 
- out_activation_:输出激活函数的名称。

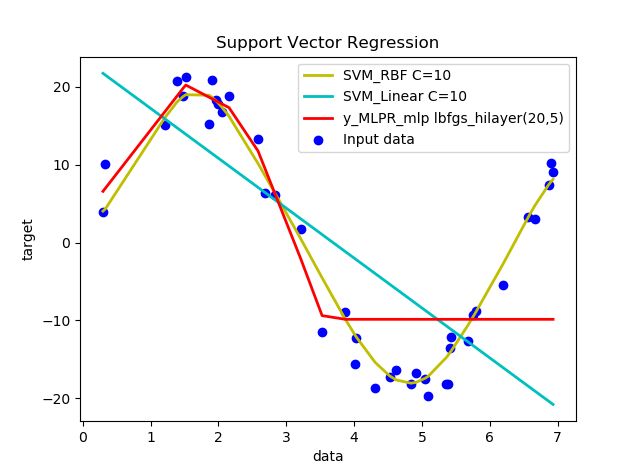
#coding=utf-8
import numpy as np
from sklearn.svm import SVR
from sklearn.neural_network import  MLPRegressor
import matplotlib.pyplot as plt

# #############################################################################
# Generate sample data
X = np.sort(7 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel() * 20
# #############################################################################
# Add noise to targets
noise = 9 * (0.5 - np.random.rand(40))
y_noise = y + noise
# #############################################################################
# Fit regression model
svr_rbf = SVR(kernel='rbf', C=10)
svr_lin = SVR(kernel='linear', C=10)
mlp=MLPRegressor(solver='lbfgs',hidden_layer_sizes=(5,2))
y_SVM_rbf = svr_rbf.fit(X, y_noise).predict(X)
y_SVM_lin = svr_lin.fit(X, y_noise).predict(X)
y_MLPR_mlp = mlp.fit(X, y_noise).predict(X)

# #############################################################################
# Look at the results
lw = 2
plt.scatter(X, y_noise, color='b', label='Input data')
plt.plot(X, y_SVM_rbf, color='y', lw=lw, label='SVM_RBF C=10 ')
plt.plot(X,y_SVM_lin, color='c', lw=lw, label='SVM_Linear C=10')
plt.plot(X, y_MLPR_mlp, color='r', lw=lw, label='y_MLPR_mlp lbfgs_hilayer(5,2)')
plt.xlabel('data')
plt.ylabel('target')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

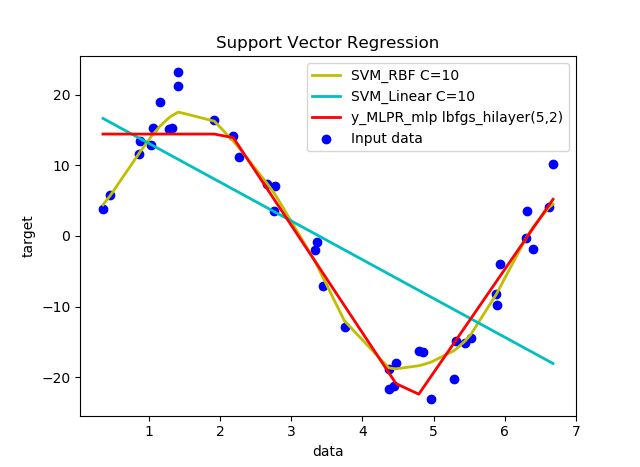
上图两层隐含层，隐层1有5个神经元，隐层2有2个神经元

上图两层隐含层，隐层1有20个神经元，隐层2有5个神经元

上图一层隐含层，隐层100个神经元

引用:

https://blog.csdn.net/suibianshen2012/article/details/51502797

https://blog.csdn.net/a819825294/article/details/51177435?locationNum=6

https://blog.csdn.net/zhongjunlang/article/details/79488955

https://blog.csdn.net/u011311291/article/details/78743393