python 战棋游戏代码实现(2):六边形地图寻路和显示

六边形地图介绍

之前的文章 生物行走和攻击选择 实现了简单的方格地图，战棋游戏一般是使用六边形地图，六边形地图的显示和寻路会更加复杂些，所以这边自己尝试增加了六边形地图的实现。
图1
六边形地图有2种形式，这里采用上面图1的形式。

地图的坐标还是采用二维数组，如下面图2所示，六边形里面的（x, y) 表示在地图数组中的坐标。
注意一点：奇数行的六边形数会比偶数行少一，比如图2中第0行有10个六边形，第1行有9个六边形。
图2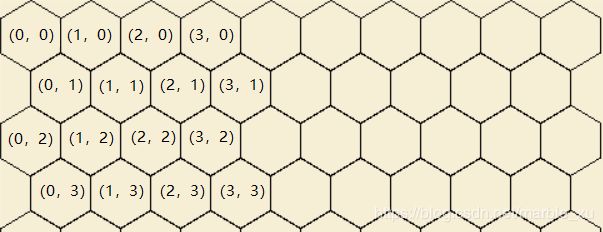

生物的行走范围如图3所示，图3 中的步兵行走范围属性值是4，表示可以走4个六边形，图中背景是深蓝色的方格就是该步兵可以走的格子，可以一步走到相邻的6个格子。
图3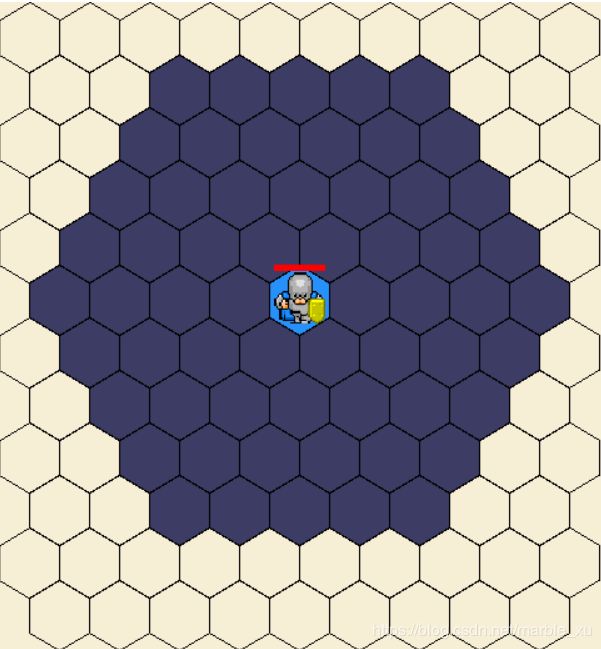

游戏截图如下：
图4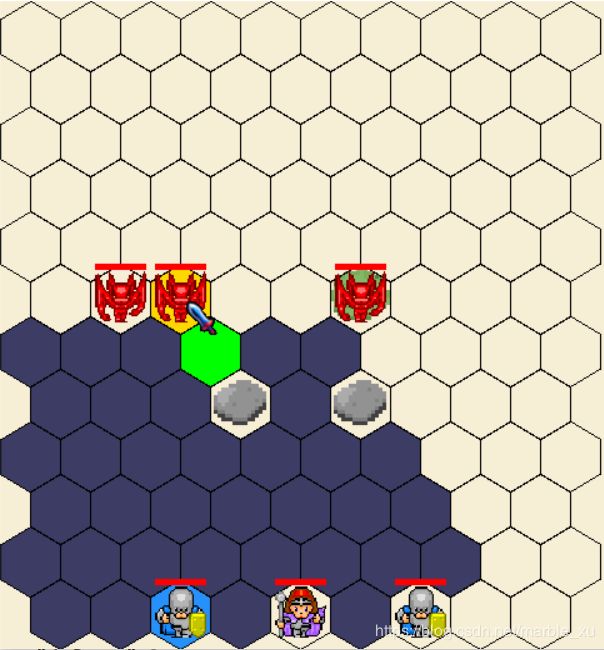
图4中，目前轮到行动的生物是我方的左下角背景为浅蓝色的步兵，可以看到背景为深蓝色的六边形为步兵可以行走的范围。背景为绿色的六边形为目前选定要行走到得方格。鼠标指向敌方生物，如果敌方生物背景六边形颜色变成黄色，表示可以攻击。图中还有石块，表示不能移动到的格子。

代码介绍

地图六边形显示

看下如何在代码中实现图1的六边形显示，这边使用的pygame的绘制多边形的函数pygame.draw.polygon() 来设置六边形的背景色，绘制连续线段的函数pygame.draw.lines() 来画六边形的黑色边。

pygame.draw.polygon()
draw a polygon
polygon(surface, color, points) -> Rect
    points (tuple(coordinate) or list(coordinate)):
       -- a sequence of 3 or more (x, y) 

pygame.draw.lines()
draw multiple contiguous straight line segments
lines(surface, color, closed, points) -> Rect

points的使用可以看下面drawBackgroundHex函数中的例子，points 列表保存了六边形六个顶点的坐标。
图5
如图5所示，红色长方形里面的六边形，先根据该六边形的坐标计算出左上角红点的值（base_x, base_y)，HEX_X_SIZE 和 HEX_Y_SIZE 分别表示红色长方形的宽度和长度。
getHexMapPos函数计算出给定坐标的左上角红点的值，可以看到奇数行相对偶数行的x值会有X_LEN的偏移（即长方形的宽度的一半）。计算y值时也是按照奇数行或偶数行分别计算。

HEX_Y_SIZE = 56
HEX_X_SIZE = 48
def getHexMapPos(x, y):
    X_LEN = c.HEX_X_SIZE // 2
    Y_LEN = c.HEX_Y_SIZE // 2
    if y % 2 == 0:
        base_x = X_LEN * 2 * x
        base_y = Y_LEN * 3 * (y//2)
    else:
        base_x = X_LEN * 2 * x + X_LEN
        base_y = Y_LEN * 3 * (y//2) + Y_LEN//2 + Y_LEN
    return (base_x, base_y)

drawBackgroundHex 函数计算出六边形所在长方形的左上角顶点值 (base_x, base_y) 后，就可以根据固定的偏移量，计算出六边形六个顶点的值, 具体的偏移量可以按照图5上的示例算出来。

    def drawBackgroundHex(self, surface):
        Y_LEN = c.HEX_Y_SIZE // 2
        X_LEN = c.HEX_X_SIZE // 2

        pg.draw.rect(surface, c.LIGHTYELLOW, pg.Rect(0, 0, c.MAP_WIDTH, c.MAP_HEIGHT))

        for y in range(self.height):
            for x in range(self.width):
                if self.bg_map[y][x] == c.BG_EMPTY:
                    color = c.LIGHTYELLOW
                elif self.bg_map[y][x] == c.BG_ACTIVE:
                    color = c.SKY_BLUE
                elif self.bg_map[y][x] == c.BG_RANGE:
                    color = c.NAVYBLUE
                elif self.bg_map[y][x] == c.BG_SELECT:
                    color = c.GREEN
                elif self.bg_map[y][x] == c.BG_ATTACK:
                    color = c.GOLD

                base_x, base_y = tool.getHexMapPos(x, y)
                points = [(base_x, base_y + Y_LEN//2 + Y_LEN), (base_x, base_y + Y_LEN//2),
                          (base_x + X_LEN, base_y), (base_x + X_LEN * 2, base_y + Y_LEN//2),
                          (base_x + X_LEN * 2, base_y + Y_LEN//2 + Y_LEN), (base_x + X_LEN, base_y + Y_LEN*2)]
                pg.draw.polygon(surface, color, points)

        surface.blit(self.map_image, self.rect)

        for y in range(self.height):
            for x in range(self.width):
                if y % 2 == 1 and x == self.width - 1:
                    continue
                base_x, base_y = tool.getHexMapPos(x, y)
                points = [(base_x, base_y + Y_LEN//2 + Y_LEN), (base_x, base_y + Y_LEN//2),
                          (base_x + X_LEN, base_y), (base_x + X_LEN * 2, base_y + Y_LEN//2),
                          (base_x + X_LEN * 2, base_y + Y_LEN//2 + Y_LEN), (base_x + X_LEN, base_y + Y_LEN*2)]
                pg.draw.lines(surface, c.BLACK, True, points)

A*算法的六边形寻路修改

A* 算法的代码实现可以看我之前的一篇文章 A*算法实现
针对六边形地图的实现修改比较简单，就修改2个函数。
getMovePositions函数获取当前位置可以移动的格子，从 图2 可以看到奇数行和偶数行格子的相邻坐标是不一样的。

 def getMovePositions(x, y):
    if c.MAP_HEXAGON:
        if y % 2 == 0:
            offsets = [(-1, 0), (-1, -1), (0, -1), (1, 0), (-1, 1), (0, 1)]
        else:
            offsets = [(-1, 0), (0, -1), (1, -1), (1, 0), (0, 1), (1, 1)]

calHeuristicDistance函数用来估计两个坐标之前的位置，注意两个坐标间X轴的距离计算：如果X轴距离小于Y轴距离的一半，就可以忽略，否则需要减去Y轴距离一半的值。

   def calHeuristicDistance(self, x1, y1, x2, y2):
       if c.MAP_HEXAGON:
           dis_y = abs(y1 - y2)
           dis_x = abs(x1 - x2)
           half_y = dis_y // 2
           if dis_y >= dis_x:
               dis_x = 0
           else:
               dis_x -= half_y
           return (dis_y + dis_x)

如图6所示举两个计算距离的例子，

• 从坐标A(0,0) 到坐标B(1,3) 的距离, 在图中可以看到按照红色线移动的距离是3 。两点间X轴距离是1，Y轴距离是3，X轴距离小于Y轴距离的一半，所以X轴距离可以忽略。
• 从坐标A(0,0) 到坐标C(3,3) 的距离，在图中可以看到是两条红色线条相加，距离是5。两点间X轴距离是3，Y轴距离是3，X轴距离大于Y轴距离的一半（3/2=1），所以X轴距离修正为2（3 - 1）。
  图6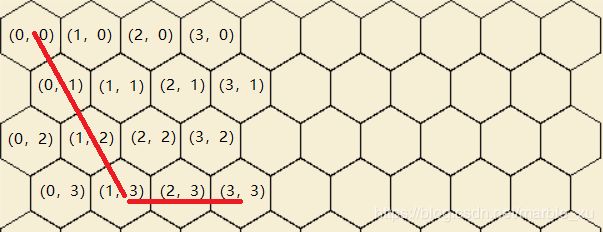

判断某个点在哪个六边形中

如何切分地图的六边形，可以有多种方式，图7中红色长方形是我采用的切分方式，长方形的宽度是六边形的宽度 (HEX_X_SIZE)，长方形的长度是六边形长度的1.5倍(HEX_Y_SIZE/2 * 3)
图7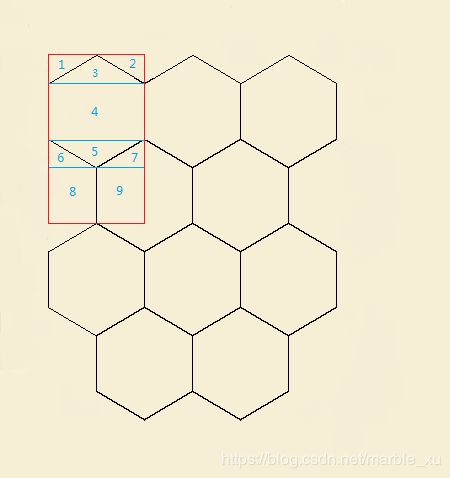
从图7出看到红色长方形里面有分成9个小的三角形或长方形区域。假设 编号3，4，5所在六边形的坐标为(map_x, map_y), 那么按照图2上的坐标可以算出：

• 编号1所在六边形的坐标为(map_x-1, map_y-1)
• 编号2所在六边形的坐标为(map_x, map_y-1)
• 编号6，8所在六边形的坐标为(map_x-1, map_y+1)
• 编号7，9所在六边形的坐标为(map_x, map_y+1)

getHexMapIndex函数就是具体的实现，根据Y轴的offset先分成三个区域（编号1，2，3， 4), （编号5，6，7）和（编号8，9）。先判断在哪个区域内，如果区域内有三角形，就调用isInTriangle函数判断是否在某个三角形中。

def getHexMapIndex(x, y):
    X_LEN = c.HEX_X_SIZE // 2
    Y_LEN = c.HEX_Y_SIZE // 2
    tmp_x, offset_x = divmod(x, c.HEX_X_SIZE)
    tmp_y, offset_y = divmod(y, Y_LEN * 3)
    map_x, map_y = 0, 0
    if offset_y <= (Y_LEN + Y_LEN//2):
        if offset_y >= Y_LEN//2:
            map_x, map_y = tmp_x, tmp_y * 2
        else:
            triangle_list = [(0, 0, 0, Y_LEN//2, X_LEN, 0),
                             (0, Y_LEN//2, X_LEN, 0, c.HEX_X_SIZE, Y_LEN//2),
                             (X_LEN, 0, c.HEX_X_SIZE, 0, c.HEX_X_SIZE, Y_LEN//2)]
            map_list = [(tmp_x - 1, tmp_y * 2 -1), (tmp_x, tmp_y * 2), (tmp_x, tmp_y * 2 -1)]
            for i, data in enumerate(triangle_list):
                if isInTriangle(*data, offset_x, offset_y):
                    map_x, map_y = map_list[i]
                    break
    elif offset_y >= c.HEX_Y_SIZE:
        if offset_x <= X_LEN:
            map_x, map_y = tmp_x - 1, tmp_y * 2 + 1
        else:
            map_x, map_y = tmp_x, tmp_y *2 + 1
    else:
        triangle_list = [(0, Y_LEN + Y_LEN//2, 0, c.HEX_Y_SIZE, X_LEN, c.HEX_Y_SIZE),
                         (0, Y_LEN + Y_LEN//2, X_LEN, c.HEX_Y_SIZE, c.HEX_X_SIZE, Y_LEN + Y_LEN//2),
                         (X_LEN, c.HEX_Y_SIZE, c.HEX_X_SIZE, Y_LEN + Y_LEN//2, c.HEX_X_SIZE, c.HEX_Y_SIZE)]
        map_list = [(tmp_x - 1, tmp_y * 2 + 1), (tmp_x, tmp_y * 2), (tmp_x, tmp_y *2 + 1)]
        for i, data in enumerate(triangle_list):
            if isInTriangle(*data, offset_x, offset_y):
                map_x, map_y = map_list[i]
                break
    if map_x == 0 and map_y == 0:
        print('pos[%d, %d](%d, %d) base[%d, %d] off[%d, %d] ' % (map_x, map_y, x, y, tmp_x, tmp_y, offset_x, offset_y))
    return (map_x, map_y)

isInTriangle函数的参数是三角形的三个顶点坐标和目标坐标，通过计算顶点和目标坐标的向量乘积来判断某个点是否在三角形中。

class Vector2d():
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def minus(self, vec):
        return Vector2d(self.x - vec.x, self.y - vec.y)

    def crossProduct(self, vec):
        return (self.x * vec.y - self.y * vec.x)

def isInTriangle(x1, y1, x2, y2, x3, y3, x, y):
    A = Vector2d(x1, y1)
    B = Vector2d(x2, y2)
    C = Vector2d(x3, y3)
    P = Vector2d(x, y)
    PA = A.minus(P)
    PB = B.minus(P)
    PC = C.minus(P)
    t1 = PA.crossProduct(PB)
    t2 = PB.crossProduct(PC)
    t3 = PC.crossProduct(PA)
    if (t1 * t2 >= 0) and (t1 * t3 >= 0):
        return True
    return False

完整代码

游戏默认是使用方块地图，如果要改成六边形地图，需要修改 source\constants.py 中的参数MAP_HEXAGON 为True

MAP_HEXAGON = True

游戏实现代码的github链接 战棋游戏
这边是csdn的下载链接 六边形战棋游戏

编译运行

1.编译环境
python3.7 + pygame1.9
2.运行
直接运行根目录下的 main.py
$ python main.py