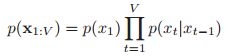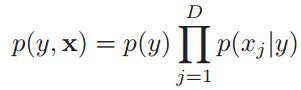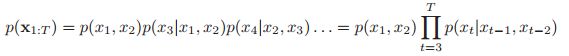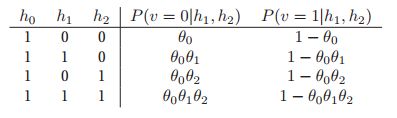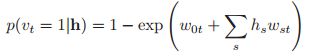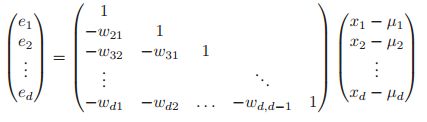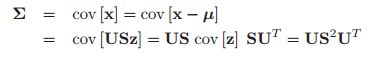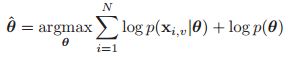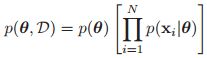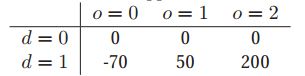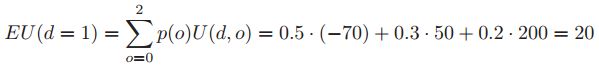MLAPP————第十章 有向图模型（贝叶斯网）

第十章 有向图模型（贝叶斯网）

10.1 简介

我基本上知道用简单的方法处理复杂系统的两个原则:第一个是模块化原则，第二个是抽象原则。我是机器学习中计算概率的辩护者，因为我相信概率论以深刻而有趣的方式实现了这两个原则。在我看来，尽可能充分地利用这两种机制似乎是机器学习的前进方向。

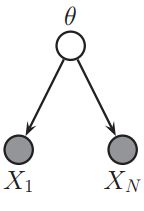
假设我们观察到很多相关的变量，比如一个文章中的单词，一幅图上的像素点或者是微阵列中的基因。那么我们怎么样才能简洁的表示出这些变量的联合分布呢？我们如何利用这个分布在合理的计算时间内推断出给定的一组变量？我们如何用合理数量的数据学习这个分布的参数?这些问题是概率建模、推理和学习的核心，也是本章的主题。

10.1.1 链式法则

通过概率论的链式法则，我们可以把一个联合分布写成如下的形式，我们按照变量的顺序来写：

这个表达式的问题是，随着t变大，表示条件分布变得越来越复杂。

举个例子，假设所有的变量都是有K个状态的话。我们可以用一个（虽然实际上K-1就行，因为所有情况求和为1，为了简单我们就用）的表来表示离散的概率分布。类似的，对于，那么我们就要用的表才能表示，所以对于最后一个条件概率分布，我们则需要才行。这些都叫做条件概率表（conditional probability tables CPTs），所以参数太多了，我们需要大量的数据来学习这么多参数。

一种解决方案就是讲CPT替换成一个更加简单的概率分布，比如在逻辑回归中，，这里后面我觉得是，这样的话，参数的数目就被压缩到了，那么整个的参数的数目就是。后面的解释我没看懂，不过我们还是关注于后面的方法。

10.1.2 条件独立

有效地表示大型联合分布的关键是对条件独立性（conditional independence CI）做一些假设。在2.2.4中我们讲过一些关于条件独立的东西和例子，X,Y关于Z是条件独立的，可以写作，体现到具体的概率分布公式上就是：

如果做出这样的假设，，用语言描述就是：考虑到现在，未来是独立于过去的。这个就称之为（first order）Markov 假设，在这样的假设下，我们的联合分布就可以写成如下的形式：

这个称之为（first order）markov链。后面17.2会详细的讲markov模型。

10.1.3 图模型

first order的markov假设对于在1维的情况下，是能够很好的处理这样的联合分布的，但是对于二维的图像，三维的视频，甚至更复杂的变量的连接关系该怎么处理呢。下面我们将引入一个叫做图模型的东西。

我们用图模型（graphical model GM）来表述在某些CI假设下的联合概率分布。在图模型中，结点表示的是随机变量，而图里面的边表示的是CI假设。实际上，这些模型的更好名称应该是独立图，但是图模型这个术语现在已经根深蒂固了。图模型也是有很多种的，有向图，无向图，或者是有向和无向图。在我们这一章，我们只考虑有向图。

10.1.4 图的术语

我们先说一下图的基本的术语和定义，其中大部分都是非常直观的。

一个图包含结点和边，其中结点是，边是。我们可以用邻接矩阵（adjacency matrix）表示图，在这个矩阵中，如果，那么我们设定。对于无向图来说，否则就是有向图。我们一般假设，这意味着一个点不能够构成一个圈。下面左边是有向图，右边是无向图。

对于有向图来说，s的父节点就是，就是带箭头的起点。

对于有向图来说，s的孩子结点就是，就是s所指向的所有结点。

对于有向图，节点的族（family）是节点及其父节点，

对于有向图，根（root）就是没有父结点的结点

对于有向图，叶子（leaf）就是没有孩子结点的结点

对于有向图，s的祖先（ancestors）就是所有能够走到s的结点，包括父结点，grand-parent结点等，即

对于有向图，s的后代（Descendants）就是s所能够走到的所有的结点，即

对于无向图来说，相连的点就叫做邻居，对于有向图来说，s点的邻居就是s点的孩子

对于一个节点来说，一个结点的邻居的个数就是这个节点的度（degree）,对于有向图来说，度分为in-degree和out-degree，分别指这个结点的父结点和孩子结点的数目。

圈或者环，对于一个无向图来说，就是能够构成一圈的，比如上图的123就构成一个圈，但是对于有向图是要看顺序的，理论上1243也连在了一起，但是由于不能按方向走回来，所以并不构成圈。

DAG(directed acyclic graph) 这个是表示没有有向环的有向图

拓扑排序（Topological ordering），对于一个DAG来说，如果其父结点的标号都比其子节点要小，那么就叫做拓扑排序的。

路径（path）就是表示从s走向t的有向的边构成的，就叫路径

树（tree）,对于一个无向图来说，树就是指没有圈的图。对于有向图来说，有向树就是DAG。

森林（forest），森林就是一系列的树。

子图（subgraph），子图就是指选取一个图的集合点A以及相应的边构成的图，。

团（Clique）,对于一个无向图来说，团是一系列结点构成的集合，这些点相互之间都是邻居。

10.1.5 有向图模型

有向图模型（directed graphical model，DGM）是一个DAG。这些通常被称为贝叶斯网络。然而，贝叶斯网络本身并没有什么贝叶斯性质:它们只是一种定义概率分布的方法。这些模型也被称为信念网络。这里的信念是指主观概率。同样，DGMs所代表的概率分布的类型本身并没有什么主观的东西。最后，这些模型有时被称为因果网络，因为有向箭头有时被解释为表示因果关系。然而，DGMs并没有内在的因果关系。出于这些原因，我们使用了更为中性(但不那么迷人)的术语DGM。出于这些原因，我们使用了更为中性(但不那么迷人)的术语DGM。就是告诉你什么贝叶斯网络，信念网络，因果网络其实都不靠谱，所以就叫DGM防止误导别人。

DAG有一个非常关键的性质，就是它一定可以进行拓扑排序，就是每一个节点的父节点是小于孩子节点的编号的。那么有了这样一个特性，我么就可以做一个叫做有序的markov 特性的假设，即：，其中就是s的父节点，就是s在排序上的前面的所有的节点。这是一阶马尔可夫性质从链到DAG的自然推广。我们还是以：

作为例子，那么我们有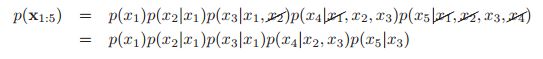：，所以说在这样的markov假设下，我们有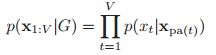。在这里，如果每个节点有K种可能性，每个节点的父节点是O（F）个，那么我们所需要的参数就是O()，这是远比要小的。

10.2 例子

在这一节中，我们将展示各种常用的概率模型可以方便地表示为DGMs

10.2.1 朴素贝叶斯分类器

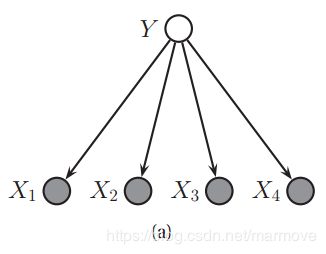
在3.5节中，我们介绍了朴素贝叶斯分类器。在朴素贝叶斯中，我们假设在给定了标签之后，特征是相互独立的。下图中显示这关于这个假设的概率图模型：

这样，我们就可以假设我们的联合概率分布可以写成如下的形式：

朴素贝叶斯假设相当朴素，因为它假定特征是有条件独立的。捕获特征之间相关性的一种方法是使用图模型。特别地，如果模型是一棵树，该方法被称为树增广朴素贝叶斯分类器（a tree-augmented naive Bayes classifier）或TAN模型，如下图：

使用树而不是一般图形的原因有两方面，首先，使用Chow-Liu算法很容易找到最优树结构，如26.3节所述，其次，很容易处理树结构模型中缺失的特性，正如我们在20.2节中解释的那样（后面会学到）。

10.2.2 markov 和 hidden markov models

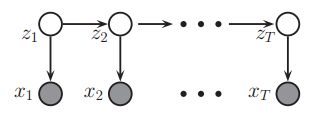
下图的(a)以DAG表示一阶马尔可夫链。当然，假设刚刚过去的，包含了我们需要知道的关于整个历史的所有信息，这个假设有点牵强。我们也可以通过在和之间增加一个依赖关系来放松它;这称为二阶马尔可夫链，如下图（b）所示。

对应的联合概率分布可以写成如下的形式：

不幸的是，如果观测值之间存在长期相关性，即使二阶马尔可夫假设也可能是不充分的。我们不能继续建立更高阶的模型，因为参数的数量会激增。另一种方法是假设有一个潜在的隐藏过程，它可以用一阶马尔可夫链来建模，但是数据是对这个过程的噪声观测(这里其实我还不太能够理解为什么是这样)。这个就叫做隐马尔科夫模型（HMM），图模型表示如下：

这里是在时间t（这里的时间指的是时刻或者是第t个顺序）的隐变量（hidden variable）以及是观测到的变量。CPD称之为转移模型，称之为观测模型。隐藏的变量通常表示感兴趣的量，例如某人当前正在说的单词的标识（在现实中有具体意义的）。观察到的变量是我们测量的，比如声波波形（物理信号）。我们要做的是在给定数据的情况下估计隐藏状态：，这个称之为状态估计（state estimation），这是概率推理的另一种形式。在17章中会详细的讲解HMM模型。

10.2.3 医疗诊断

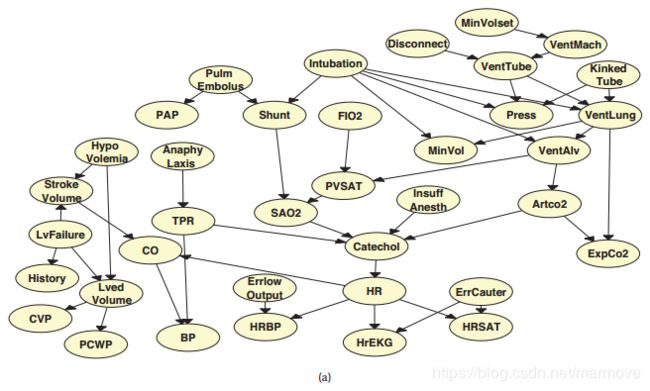
考虑为重症监护病房(ICU)中测量的各种变量之间的关系建模，例如病人的呼吸频率、血压等。下图中的警报网络是表示这些依赖关系的一种方法(Beinlich et al. 1989)。该模型有37个变量和504个参数。

由于这个模型是手工创建的，通过一个称为知识工程的过程，它被称为概率专家系统。在10.4节中，我们讨论了如何在已知图结构的情况下，从数据中学习DGMs的参数，在26章中，我们讨论了如何学习图结构本身。

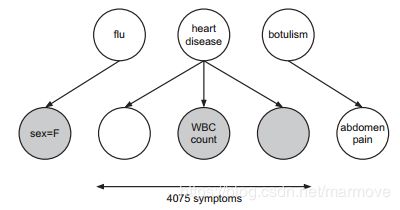
另一种医疗诊断网络，即快速医疗参考（quick medical reference）或QMR网络(Shwe et al. 1991)，如下图所示。这是为了模拟传染病。QMR模型是一个二部图结构，疾病(原因)在顶部，症状或发现在底部。

所以概率分布可以写成如下的形式：

其中表示隐变量节点(疾病)，表示可见的观测节点(症状)。

根节点的CPD只是伯努利分布，表示该疾病的先验概率。因为要么就是有这个症状，或者是没有。使用CPTs表示叶(症状)的CPD需要太多参数，因为有些病症与其相关的症状可能会非常多。另一种自然选择是使用logistic回归对CPD建模，之前我们讲过这个方法。然而，由于该模型的参数是手工创建的，因此使用了另一种CPD，noisy-OR model（没听说过）。

noisy-OR模型假定，如果父节点处于on状态，那么子节点通常也处于on状态(因为它是or-gate)，但是偶尔从父节点到子节点的链接可能会失败，这是随机（有噪声）的，这个处理方式跟名字很契合。在这种情况下，即使父进程是打开的，子进程也可能是关闭的。下面我们详细的说一下。我们令是链接失败的概率。所以是能单独激活t的概率是多少。一个孩子被关闭的唯一情况，就是他的父节点链接到它的时候都是随机关闭的。因此：

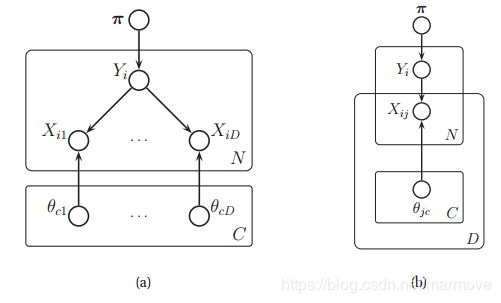
，那么很明显：。如果我们观察到但它的所有父结点都是关闭的，那么这与模型相矛盾。这样的数据案例在模型下得到的概率为零，这是有问题的，因为有可能某人表现出症状，但没有任何指定的疾病。为了处理这个问题，我们添加了一个虚构的泄漏节点h_0，它总是处于打开状态;这代表了所有其他原因（疾病）。加了这个之后，那么CDP就变成了：，下表给出了一个具体的例子：

如果我们定义：，那么我们可以重写CPD：

这其实跟logistic回归的形式是非常的像的。

用noise-or模型去做Bipartite models叫做BN2O模型。基于专业领域，它相对容易设置参数。然而，也可以从数据中学习它们。noise-OR模型cpd在模拟人类因果学习中也被证明是有用的以及一般的二进制分类设置。

10.2.4 遗传连锁分析*

10.2.5 有向高斯图模型*

如果对于一个DGM来说，它的所有的变量都是实数，并且所有的CPD具有如下的形式：

这个就叫做线性高斯CPD。下面将要说明，如果把这些CPDs都乘起来的话，我们就能够得到一个很大的联合高斯分布，即：，这个就叫做directed GGM或者高斯贝叶斯网。

下面我们将从CPD的参数中去计算。为了方便，我们改写一下：，其中。我们看到上面的模型中，是没有让parent变量减去均值，但是书中注脚说这样结果看上去会简洁很多，所以这里注意这个模型相比于上面开始的模型是减了父结点的均值的。

我们很容易看到跟巨上面定义的式子，关于求均值其实就是，所以整体的均值其实就是。下面我们推导全局的一个协方差矩阵。令是关于所有标准差构成的对角矩阵。所以就可以写成矩阵的形式：，注意这里的在不是父节点的位置上都是0。

我们记：，这是噪声项的向量。当然根据上面的式子，我们有。书上说是一个下三角矩阵，因为在拓扑结构上可以使得，对于这一点我有疑问，不是DAG才可以吗，一般的DGM是做不到这一点的吧？。我们先假设是DAG，那么我们有也是一个下三角矩阵，并且对角线上都是1。因此：

因为总是可逆的，所以，其中我们定义。因此我们有：

10.3 推理（Inference）

我们已经看到图模型提供了一种定义联合概率分布的简洁方法。对于这样的联合分布，我们能做些什么呢?这种联合分布的主要用途是执行概率推理。这是指从已知的观测到的变量中去估计未知（隐藏的）变量。例如，在10.2.2节中，我们介绍了HMMs，我们的目标之一是通过观察(例如，语音信号)来估计隐藏状态(例如，单词)。

假设我们有一组随机变量，他们的联合概率密度如下：，在这一节中，我们假设模型的参数都是已知的，下一节中，我们考虑怎么去学习这些参数。首先我们将我们上面的V个变量分成两个部分，其中一个部分是我们可以观测到的变量，即：，另一部分则是隐藏的变量。那么我们的推理就可以写成如下的条件概率分布：

分子部分的归一化常数其实就是数据的似然，我们也称之为证据概率（probability of the evidence）。有时候只有一部分隐藏变量是我们感兴趣的，所以我们再把隐藏变量分成两个部分，其中一部分叫做查询变量（query variables），这些变量的结果是我们想知道的。剩下的那些隐变量就叫做扰嚷变量，这些是我们不感兴趣的。我们可以通过边缘化讨厌的变量来计算我们感兴趣的东西：

在4.3.1节中，我们了解了如何在时间内对多元高斯函数执行所有这些操作，其中V是变量的数量。对于变量如果值是离散的，比如每个变量有K个状态，那么如果我们类似于前面把所有的条件概率都表示出来了，那么我们则需要的空间。20章有一个方法能在时间内计算好，其中w是衡量图的树宽的一个数，如果图示一个树或者链，那么w=1，那么在常数的时间内就可以解决问题。当然具体我们后面再说，当然对于一般的情况其实我们还是很难解决的，后面我们会慢慢讲到。

10.4 学习（Learning）

在图模型中，比较常见的做法就是把推理和学习分开。推理意味着计算，其中参数假设是已知的，通过观测到的变量去推测隐变量。在学习的过程中，则是利用观测到的数据，通过MAP去估计参数：

当然，如果我们使用的是uniform的先验，即，那么就变成了MLE的情况。

但是如果我们从贝叶斯的角度来看的话，贝叶斯把参数也看成是未知的变量，也应当放在推理的框架中。因此对于贝叶斯的框架来说，推理和学习是没有任何区别的。所以也可以把参数当成是变量体现在图模型中。在这个观点下，隐变量和参数的最大的区别就在于，隐变量的数量会随着数据不停的增加而增加（因为可能对于每一个观测到的数据都会有一些隐变量），但是参数的数量往往是确定不变的。由于隐变量的数目太多，所以在估计的时候很容易过拟合，所以在进行参数估计是，我们需要把隐变量给积分掉。

10.4.1 plate notation

当我们从数据中推理参数的时候，我们一般都会假设数据是独立同分布的。下图，我们利用图模型明确的表明了这个关系：

这个图表明了所有的数据都是从同一个分布中独立的生成的。所以我们的数据是没有顺序的分别，不同的顺序并不会影响关于的估计结果。我们称这些数据是可以交换的。

为了避免有人有密集恐惧症，如果1000个数据，画1000个变量也太恐怖了，所以就用一个简洁的方盒子表示，具体如下：

这就表明了这些变量是独立的，并且总共的数量是N个。

这样的话，联合概率分布就可以写成如下的形式：。

下图展示了一个更加复杂的例子，这是一个朴素贝叶斯分类器的例子：

左图是只使用一个plates的情况，而右图则是使用嵌套的plates的情况，这个图其实不难理解，把对应的标号对应起来就行了。在这个图里面有比较模糊的一个关系就是只有当，才被使用来生成。

10.4.2 从完整的数据里面学习

如果所有的变量是被完全的观测到的，即没有丢失的数据同时也没有隐变量，我们就叫这样的数据是完整的（complete）。一个具有完整数据的DGM，其似然函数如下：

其中是与节点t和它的父母节点相关的数据。这个似然函数就可以看成若干个CPD的乘积。我们说似然是根据图的结构分解的。

现在我们假设我们的先验是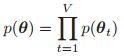：，那么我们的后验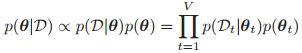：，这意味着我们可以独立计算每个CPD的后验。换句话说，先验的乘积乘上似然的乘积意味着后验的乘积。

我们考虑一个例子，其中我们的CPDs都是表格的，对于每一个conditioning case，我们都有一个各自的row。正式的，我们可以把第th CPT 写作（CAT分布就是多个结果的伯努利分布），其中，其中我们有：，就是第t个节点状态的数目，就是父亲节点的所有可能性的组合，T是所有节点的数目。很明显，对于每个节点来说。

由于我们的CPT是Cat分布，所以对于每一个单独的行的CPT，我们的选择的先验是Dirichlet分布，即：，然后我们可以通过简单地将伪计数与经验计数相加来计算后验，其中是节点t处于k状态而其父节点处于c状态的次数，即：

根据公式2.77，我们可以得到分布的均值如下：

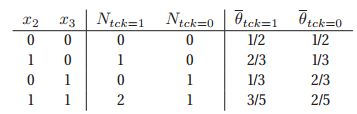
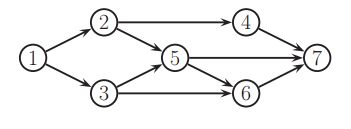
举一个具体的例子，假设我们的DGM就是书上的Fig 10.1(a)。假设我们的训练数据包含了以下的5种情况：

我们列举出第4个节点（t=4），在先验参数为的情况下（对应于add-one即拉普拉斯平滑），从而给出充分统计量以及后验均值参数。

对于MLE估计来说，那就是不需要先验信息，所以就是把书中式子10.32中的给去掉就好了，但是往往这个先验还是很有必要的，因为对于没有发生的事件，将概率直接置为0并不是一个好的选择。

10.4.3 对于有缺失数据或者存在隐变量情况下的学习

如果我们有一些缺失的数据，或者说隐变量，我们在后面11.3节中将会提到，我们的似然函数并不能再写成factored的形式，并且也不再是凸的。这意味着我们通常利用ML或者MAP只能获得局部最优值。参数的贝叶斯推理更加困难。我们将在后面几章讨论适当的近似推理技术。在后面的几章当中，我们将会介绍一些合适的近似推理方法。

10.5 DGMs的条件独立特性

任何的DGM的核心就是一堆条件独立（CI）的假设。如果在图G中，A和B关于C条件独立，我们就记作：。我们令就是由图G的所有的CI假设构成的集合（每一个条件独立的假设就是集合中的一个元素）。

如果我们有，其中就是概率p中所有的CI假设构成的集合，那么我们就称G是关于p的I-map，或者说是p关于G是markov的。也就是说如果G是p的I-map，那么G中的所有CI都是在p中存在的，是符合p的，但是p中有些条件独立的假设，在G中可能就被忽视了。

一个全联通的图一定是所有分布的I-map，因为它没有任何的CI假设。所以我们往往要找一个minimal I-map，如果G是一个minimal I-map，那么意味着不存在一个I-map，G'，有。

对于无向图来说，定义是非常简单的，但是对于有向图来说，可能还是会有一些复杂。

10.5.1 d-分离和贝叶斯球算法（全局markov特性）

首先我们介绍一些定义。假设一个没有方向的路径P(undirected path P)满足以下的三个条件之一：

1. P包含一个链（chain），或者，其中

2. P包含一个叉，，其中

3. P包含一个v结构，，其中m不在E中，m的任何子结点也不在E中。

那么我们就称P是关于节点集合E的d-分离(d-separated)。

对于一个节点集合A以及一个节点集合B还有一个给定的节点集合E，如果A中的每一个节点a到B中的每一个节点b的无向路径P是关于Ed-分离的。那么最终我们定义DAG的CI特性为：。这里我之前还在想为什么用DAG而不是DGM，因为DGM可能以上的规则并不太充分，后面贝叶斯球提供的规则可能会有点问题。

贝叶斯球是一个简单的方法去看A是否是关于E独立于E的。想法就是，我们将我们观测到的节点即E全部都用灰色的圆圈来表示。然后我们给A里面的每一个节点放一个球，让他们根据一定的规则运动，看A里面的球是否能够运动到B里面去，如果不能的话说明是独立的。具体的规则如下图：

其中箭头撞到墙上的就是过不去，带阴影的就是过得去，我们发现就是（a）,（b）,（f）这三个情况是条件独立或者独立的。其余都不是，所以我们怎么看，那就是把G中的E全涂成灰色，然后看是否A中所有的点都是到不了B的，如果是的，那么这个就是成立的。

我们可以去证明贝叶斯球的这些规则。首先我们先来证明一个链结构：，那么概率密度函数写为：，那么我们继续对式子进行进一步推导，我们把y看做是已知的：

因此我们有：，所以观察链的中间节点会把它分成两部分(就像马尔可夫链一样)。

现在考虑tent结构：，联合分布具有如下的形式：，根据进一步的推导，我们有：

因此，因此，观察根节点分离其子节点(如朴素贝叶斯分类器中:参见3.5节)。

最后，我们考虑v结构：。那么联合分布就是：，我们假设y是已知的，有：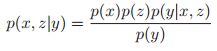

所以，然而在非条件的情况下，我们有，我们看到x和z是边缘独立的。所以我们看到，当v型结构底部的孩子是已知的话，那么他们的父母就是相互依赖的。这种重要的影响被称为explaining away，inter-causal reasoning，或伯克森悖论。找一个例子来解释一下，假设我们抛两个硬币，代表二进制数0和1，我们观察它们的值的和。根据先验，硬币是独立的，但是一旦我们观察到它们的和，它们就成为耦合的(例如，如果和是1，而第一枚硬币是0，那么我们就知道第二枚硬币是1)。

书的下一段又表明了关于一些边界条件，但是这里我看到网上有一个博客关于贝叶斯球的路径规则总结的非常好，我就copy下来：

首先定义几个术语：
通过（pass through）：从当前结点的父节点方向过来的球，可以访问当前结点的任意子节点。（父 -> 子）
                                      从当前结点的子节点方向过来的球，可以访问当前结点的任意父节点。（子 -> 父）
反弹（bounce back）：从当前结点的父节点方向过来的球，可以访问当前结点的任意父节点。（父 -> 父）
                                      从当前结点的子节点方向过来的球，可以访问当前结点的任意子节点。（子 -> 子）
截止（block）：当前结点阻止贝叶斯球继续运动。

3.规则
    一个结点可以是已知结点或未知结点，现在使用术语来描述贝叶斯球在这两种结点上的运动规则：

   未知结点：总能使贝叶斯球通过，同时还可以反弹从其子节点方向来的球。（父 -> 子）|（子 -> 父/子）

   已知结点：反弹从其父节点方向过来的球，截止从其子节点方向过来的球。（父 -> 父）|（子 ->“截止”）

上述规则如下图所示，单圈表示未知结点，双圈表示已知结点：

10.5.2 其它的关于DGMs的markov特性

根据d-separation准则，我们可以得到如下的结论：（有向局部马尔可夫性质  directed local Markov property），其中nd(t)是一个图的t节点的非后代节点，体现在公式上就是：。

该属性的一个特殊情况是，我们只根据DAG拓扑顺序查看节点的前一个节点。我们有：，这个是显然成立的，因为，这个被称之为有序的markov特性。举个例子，对于下图来说：

如果我们使用顺序1,2,3...7。我们发现，，所以。

我们现在已经描述了DAGs的三个markov性质，一个是directed global Markov property G，书中的10.34，第二个是the ordered Markov property O，书中的10.43。第三个是the directed local Markov property L，书中的10.42。看上去比较明显的推理过程是，但是实际上其实是，具体可以参照（see e.g., (Koller and Friedman 2009) for the proof）。

10.5.3 Markov blanket and full conditionals（不知道怎么翻译）

Markov blanket的定义是：

书上的那个一开始没翻译懂，这是网上的一个博客写的。书上把这里的X记作t，MB记作mb(t)。可以证明DGM中节点的马尔可夫毯子等于父节点 子节点和共同父节点（即也是它的子节点的父节点的那些节点）。例如对于书上的图10.11也就是上面那个DAG来说，。

为什么说在markov blaket里面要加入co-parents这一项呢，注意到我们在推导，有，我们把不含有的这些常数项全部给扔掉，那么我们就有，我们发现，就跟我们上面说的三个有关，父结点，孩子结点，以及近亲节点。所以说在这些节点已知的情况下，t和其他的那些节点其实是独立的，所以这也就证明了我们的markov毯为什么是这样的。例如，书上图10.11，我们有，这个东西其实就叫做节点t的full conditionals，这个在后面的吉布斯采样中会非常的重要。

10.6 影响（决策）图

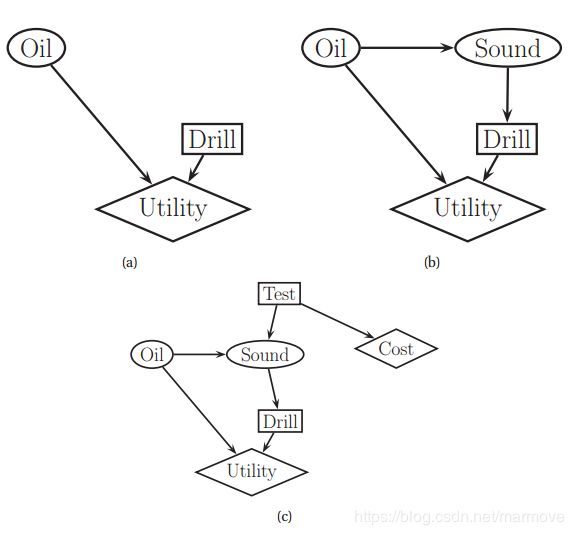
我们可以使用一种称为决策图或影响图的图形符号来表示多阶段(贝叶斯)决策问题。它通过添加决策节点(也称为操作节点)(由矩形表示)和实用节点(也称为值节点)(由菱形表示)来扩展有向图模型。原始的随机变量称为随机节点，通常用椭圆表示。

下图（a）给出了一个简单的例子，说明了著名的oil wild-catter问题。

在这个问题上，你必须决定是否钻井。有两种可能的操作:d = 1表示钻，d = 0表示不钻。你假设有三种自然状态:o = 0表示井是干的，o = 1表示井是湿的(有一些油)，o = 2表示井是浸泡的(有很多油)。假设你先前的先验是p(o) =[0.5, 0.3, 0.2]。最后，您必须指定实用函数U(d, o)。由于状态和操作是离散的，我们可以将其表示为表(类似于DGM中的CPT)。

我们看到，如果你不钻井，你就没有成本，但也赚不到钱。如果你钻一口干井，你会损失70美元;如果你钻一口潮湿的井，你会得到50美元;如果你钻一口浸泡井，你会得到200美元。所以你钻井的期望的收益是：

不钻取的期望收益是0。最大期望收益是：因此，最佳的行动是钻孔：。

现在让我们考虑对该模型的稍微扩展。假设你执行一个测深来估计井的状态。测深观测可以是三种状态之一:s = 0为漫反射模式，表示无油;s = 1为开反射模式，说明有油;s = 2是一个闭合的反射图形，表示有大量的油。由于S是由O引起的，所以我们在模型中添加了一个弧。此外，我们假定在决定是否钻井之前，测深试验的结果是可用的;因此，我们添加了一个从的信息弧，如上图(b)所示。

让我们用以下的条件分布对传感器的可靠性建模:

假设我们做探测测试，我们观察到s = 0。关于油井状态的后验就是：。那么这个时候你采取相应的措施所获得后验期望收益就是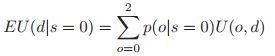：，如果d=1的话，这就表明：，然而如果d=0的话，那么，所以如果我们探测到s=0，我们最好就不要去钻井了。

现在假设我们做探测测试，我们观察到s = 1。同理，可以看出，高于。同样的，如果我们观察s = 2，我们得到，这比要高得多。因此，最优策略为:如果s = 0，选择，得到$0;如果s = 1，选择，得到$32.9;如果s = 2，选择，得到$87.5。

你可以计算你的期望利润或最大期望效用如下:，关于s的先验可以通过如下的方式计算得到。

因此，您的最大期望效用是：。

现在假设你可以选择是否做这个测试。如上图(c)所示，我们在其中添加了一个新的测试节点T。如果T = 1，我们进行测试，S可以进入由O决定的3种状态中的1种，正如上面所述。如果T = 0，我们不做测试，S进入一个特殊的未知状态。执行测试还需要一些成本。

做这个测试值得吗?这个取决于做了决策之后MEU会发生多大的变化。如果你没有做这个测试，那么从公式10.49我们可以得到MEU = 20。如果你做这个测试，那么根据公式10.56，我们有MEU = 32.2。因此，如果您进行测试(并对其结果采取最优行为)，那么效用的改进是12.2美元。这称为完全信息值(VPI)。所以我们应该做这个测试，只要它的成本低于12.2美元。

在图模型方面，变量T的VPI可以通过计算基本影响图I的MEU来确定，然后再计算相同影响图的MEU，将信息弧线从T添加到动作节点，然后计算其差值。换句话说：

其中D是决策节点，T是我们要测量的变量。后面还有一部分的相关延伸我就先不写了，暂时我觉得我还不能理解到那一步。