贪心算法的几种经典例题

什么是贪心算法

贪心算法是一种在解决问题的过程中追求局部最优的算法，对于一个有多种属性的事物来说，贪心算法会优先满足某种条件，追求局部最优的同时希望达到整体最优的效果。以背包问题为例，可以放在背包中的物体有它的重量和价值两种属性，背包的容量也是有限的，我们希望得到一种价值最大的物品摆放方式，如果我们倾向于重量贪心，那么在摆放物品的时候会优先放重量小的，但这和我们追求的价值最优没有关系，自然不能采用；如果倾向于价值贪心，而忽略了物品的重量，可能会导致摆放物品的数量不多，总价值很小；如果是以价值和重量的比值设计贪心算法求解，便可以实现最优的方案。下面我们举一些例子来说明在实际运用中如何实践贪心算法。

例题1：钱币找零问题

1、题目：指定币值和相应的数量，用最少的数量凑齐某金额。
2、思路：利用贪心算法，我们优先选择面值大的钱币，以此类推，直到凑齐总金额。
3、算法实现：

   /**
     * 贪心算法1：钱币找零问题
     */
	public void greedy1(){        
                       //面额
			int[] values = { 1, 2, 5, 10, 20, 50, 100 };
			//数量
			int[] counts = { 3, 3, 2, 1, 1, 3, 3 };
			//获取需要各种面值多少张
			int[] result = getNumber1(446, values, counts);             
			System.out.println("各币值的数量："+Arrays.toString(result));
	}

	/**
	 * 贪心算法1：钱币找零问题
	 * @param sum
	 * @param values
	 * @param counts
	 * @return
	 */
	public int[] getNumber1(int sum , int[] values, int[] counts)
	{
		int[] result = new int[7];
		int add=0; //当前凑的金额
		for(int i=values.length-1;i>=0;i--)
		{
		    int num = (sum-add)/values[i];
		    if(num>counts[i])
		    {
		    	num=counts[i];
		    }
			add=add+num*values[i];
	        result[i]=num;
		}
		return result;		
	}

例题2：活动选择问题

1、题目： 有n个需要在同一天使用同一个教室的活动a1,a2,…,an，教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi ，一旦被选择后，活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠，ai和aj两个活动就可以被安排在这一天，该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。例如下图所示的活动集合S，其中各项活动按照结束时间单调递增排序。

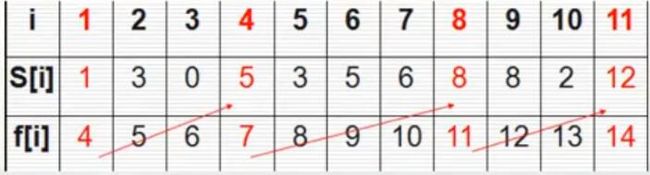
2、思路：使用贪心算法，目标是实现安排尽可能多的活动，那么我们优先找那些结束时间早的活动，为后面的活动留出更多时间，即以结束时间为贪心。
3、算法实现：
注：这里我们稍打乱了顺序，在代码中采用了插入排序的方法对数据简单整理，使得结束时间从小到大排列。

	/**
	 * 贪心算法2：活动选择问题
	 */
	public void greedy2(){		  
			   int [] st = {1,5,0,5,3,3,6,8,8,2,12};
			   int [] et = {4,9,6,7,8,5,10,12,11,13,14};			
			   int num = getNumber2(st,et);
			   System.out.println("活动数量："+num);		
	}
	/**
	 * 贪心算法2：活动选择问题
	 * @param a
	 * @param b
	 * @return
	 */
	public int getNumber2(int[] a , int[] b)  //优先选择结束时间早的
	{
		int num=0;
		int tempa=0;
		int tempb=0;
		int endTime=0;
		int j=0;
		for(int i=1;i<b.length;i++)//如果顺序混乱，则调整为结束时间从小到大的顺序,直接插入排序
		{
			    tempb=b[i];
				tempa=a[i];
			for(j=i-1;j>=0&&tempb<b[j];j--)
			{								
					b[j+1]=b[j];
					a[j+1]=a[j];
					if(j==0)
					{
						j--;
						break;
					}
			}
			    b[j+1]=tempb;
				a[j+1]=tempa;				
		}
		System.out.println(Arrays.toString(a));
		System.out.println(Arrays.toString(b));		
		num++;
		endTime=b[0];
		for(int k=1;k<b.length;k++)
		{
			if(a[k]>endTime)
			{
				num++;
				endTime=b[k];				
			}
		}						
		return num;								
	   }	
     }

例题3：背包问题

1、题目：现有几种拥有一定重量和价值两个属性的物品，需要放到一个容量一定（能承受的重量一定）的包中，物品放入包中时，物品可以不完全放入包中，而放入一部分，求价值最大的方案。
2、思路： 背包问题一般不能使用贪心算法。 然而我们考虑这样一种背包问题：在选择物品i装入背包时，可以选择物品的一部分，而不一定要全部装入背包。这时便可以使用贪心算法求解了。 计算每种物品的单位重量价值作为贪心选择的依据指标，选择单位重量价值最高的物品，将尽可能多的该物品装入背包，依此策略一直地进行下去，直到背包装满为止。 在零一背包问题中贪心选择之所以不能得到最优解原因是贪心选择无法保证最终能将背包装满，部分闲置的背包空间使每公斤背包空间的价值降低了。 在程序中已经事先将单位重量价值按照从大到小的顺序排好。
3、算法实现：

	/**
	 * 贪心算法3：背包问题
	 */
	public void greedy3(){
			    float M=50;  
			    //背包所能容纳的重量     
			    float[] w={0,10,30,20,5};  
			    //每种物品的重量    
			    float[] v={0,200,400,450,20};    
			    //每种物品的价值   
				   
				float num = getNumber3(M,w,v);   
				 
				System.out.println("物品数量："+num);
	}
	/**
	 * 贪心算法3：背包问题
	 * @return
	 */
	public float getNumber3(float M,float[] w ,float[] v)
	{
		float num=0;
		int i=0;
		float max=0;
		float weight=0;
		for(i=0;i<w.length;i++)
		{
			if(v[i]/w[i]>max)
			{
				max=v[i]/w[i];
				weight=w[i];
			}
		}
		num=M/weight;
		return num;	
	}

例题4：多机调度问题

1、题目：n个作业组成的作业集，可由m台相同机器加工处理。要求给出一种作业调度方案，使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
2、思路：作业不能拆分成更小的子作业；每个作业均可在任何一台机器上加工处理。 这个问题是NP完全问题，还没有有效的解法(求最优解)，但是可以用贪心选择策略设计出较好的近似算法(求次优解)。当n<=m时，只要将作业时间区间分配给作业即可；当n>m时，首先将n个作业从大到小排序，然后依此顺序将作业分配给空闲的处理机。也就是说从剩下的作业中，选择需要处理时间最长的，把它分配给当前总累计需要工作时长最短的机器。这样一来，这个调度问题可以理解为一个分配问题，我们通过这种方案，使得几台机器获得接近的工作总时长，达到整体的最短的工作时长的效果。
3、算法实现：

	/**
	 * 贪心算法4：多机调度问题
	 */
	public void greedy4()
	{
		       int[] time= {9,7,8,4,2,1,3};
		       int number = 3;
		       
		       int Sumtime = getNumber4(time,number);
		
		       System.out.println("花费的最小总时间："+Sumtime);		
	}
	 /**
	 * 贪心算法4：多机调度问题
	 * @param time
	 * @param number
	 * @return
	 */
	public int getNumber4(int[] time, int number)
	{
		int usedTime=0;  //最长时间为总时间
		int[] fin = new int[number]; //单机处理时间		
		for(int k=0;k<number;k++) //初始时间清零
		{
			fin[k]=0;
		}		
		if(number>time.length)
			return time[0];
		else 
		{			
			for( int i=0 ; i<time.length-1 ;i++)
			{  
				   for( int j=0;j<time.length-i-1;j++) //冒泡选出任务时间最大的
				   {
					   if(time[j]>time[j+1])
					   {
						   int temp = time[j+1];
						   time[j+1]=time[j];
						   time[j]=temp;
					   }
				   }
					   int min=0;; 
					   int value=100;
					   for(int k=0;k<fin.length;k++)  //选出当前累计工时最小的机子
					   {
						   if(fin[k]<value)
						   {
							   min=k;
							   value=fin[k];
						   }						  
					   }					   						
					   fin[min]+=time[time.length-1-i];							   
			} 
			   int min=0;; 
			   int value=100;
			   for(int k=0;k<fin.length;k++)  //选出当前累计工时最小的机子
			   {
				   if(fin[k]<value)
				   {
					   min=k;
					   value=fin[k];
				   }				  
			   }
			   fin[min]+=time[0];
			for( int n=0;n<fin.length;n++)
			{
				if(fin[n]>usedTime)
				{
					usedTime=fin[n];
				}
			}
			return usedTime;
		}		
	}

贪心算法5：小船过河问题

1、题目：N个人过河，船每次只能坐两个人，船载每个人过河的所需时间不同t[i]，每次过河的时间为船上的人的较慢的那个，求最快的过河时间。(船划过去要有一个人划回来)
2、思路：本题的最优选择是先将所有人过河所需的时间按照升序排序。优先把速度慢的人带到对岸，返回由速度快的人来完成，节省时间，在剩余人数大于3时，有两种方式： 1.最快的和次快的过河，然后最快的将船划回来；次慢的和最慢的过河，然后次快的将船划回来，所需时间为：t[0]+2t[1]+t[n-1]；2.最快的和最慢的过河，然后最快的将船划回来，最快的和次慢的过河，然后最快的将船划回来，所需时间为：2t[0]+t[n-2]+t[n-1]。最后还需处理一下人数小于等于3的边界问题。
3、算法实现：

	/**
	 * 贪心算法5：小船过河问题
	 */
	public void greedy5()
	{
		       int[] v = {1,3,4,8,4,3,9}; //按照不同的人的速度过河所需的时间
		       int timeSum=getNumber5(v);
		       System.out.println("过河总时间："+timeSum);
	}
          /** 
	 * 贪心算法5：小船过河问题
	 */
	public int getNumber5(int[] v)
	{
		int time =0;;
		Arrays.sort(v);//降序排列
		int N = v.length; //N表示当前人数
		while(N>3)
		{
			if(2*v[0]+v[N-1]+v[N-2]>2*v[1]+v[0]+v[N-1])
				time+=2*v[1]+v[0]+v[N-1];
			else
				time+=2*v[0]+v[N-1]+v[N-2];
			N-=2;
		}
		else if(N==3) //处理边界
		{
			time+=v[2]+v[0]+v[1];
		}
		else if(N==2)
		{
			time+=v[1];
		}
		else if(N==1)
		{
			time+=v[0];
		}	
		return time;		
	}

总结

贪心算法追求局部最优，拿到问题之后先分析我们需要达到什么目标，是否适合采用贪心算法，并且使得什么最优以及实现的方法。