《机器学习实战》和Udacity的ML学习笔记之 Ensemble Learning 集成学习
转载自:Ensemble learning(集成学习)
这篇博问对集成学习的解释比较浅显易懂,主要知识点如下:
- 集成学习的概念及其原理
- 集成学习的步骤
- 如何构建有差异的分类器
- 如何对分类器进行整合为一个实例进行分类
学习器为什么可以提高预测精度(降低偏差)
关于最后一点,作者并没有从理论的角度进行分析,实质上涉及到子模型和模型偏差和方差的问题,具体到不同地算法对应的情况也不一样。具体而言,降低偏差的是集成学习中的boosting算法,而bagging算法子模型的偏差(精度)和最终的模型差不多(不会有多大提升),但是有于样本数量问题,很可能出现欠拟合,通过综合子模型以增大模型覆盖范围,从而降低模型方差。
具体原因及原理可参考:
1.使用sklearn进行集成学习——理论
2.为什么说bagging是减少variance,而boosting是减少bias?
更多参考内容(算法原理及其编码):
1.机器学习实战笔记7(Adaboost)
2.利用AdaBoost元算法提高分类性能
主要内容是集成学习的主要算法Adboost(自适应提升)的原理。即如何给错误率高数据的赋更多的权值,以增加迭代弱分类器对上一个分类器错分数据的注意。
原博文:
集成学习:是目前机器学习的一大热门方向,所谓集成学习简单理解就是指采用多个分类器对数据集进行预测,从而提高整体分类器的泛化能力。
我们在前面介绍了。所谓的机器学习就是通过某种学习方法在假设空间中找到一个足够好的函数h逼近f,f是现实数据的分布函数模型,这个近似的函数就是分类器。
我们以分类问题作为说明,分类问题指的是使用某种规则进行分类,实际上就是寻找某个函数。集成学习的思路大体上可以这样理解:在对新的数据实例进行分类的时候,通过训练好多个分类器,把这些分类器的的分类结果进行某种组合(比如投票)决定分类结果,以取得更好的结果,就是我们生活中那句话“三个臭皮匠顶个诸葛亮”,通过使用多个决策者共同决策一个实例的分类从而提高分类器的泛化能力。
当然通过这种集成学习提高分类器的整体泛化能力是有条件的:
1)分类器之间应该具有差异性,想想看啊,如果使用的是同一个分类器,那么集成起来的分类结果是不会有变化的。
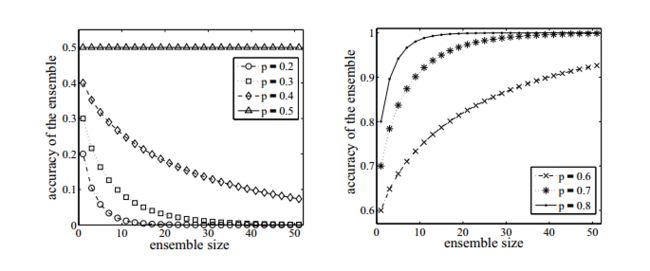
2)分类器的精度,每个个体分类器的分类精度必须大于0.5。如下面的图,可以看到如果p<0.5,那么随着集成规模的增加,分类精度会下降,但是如果大于5的话,那么最终分类精准度是可以趋于1的。
因此集成学习的关键有两点:
1)如何构建具有差异性的分类器 2)如何多这些分类器的结果进行整合。
1.构建差异性基分类器
(1)通过处理数据集生成差异性分类器
这种方法实际就是在原有数据集上采用抽样技术获得多个训练数据集,从而生成多个差异性分类器。流行的方法有装袋(bagging)和提升(boosting)。
bagging:通过对原数据集进行有放回的采用构建出大小和原数据集D一样的新数据集D1,D2,D3…..,然后用这些新的数据集训练多个分类器H1,H2,H3….。因为是有放回的 采用所以一些样本可能会出现多次,而其他样本会被忽略,理论上新的样本会包括67%的原训练数据。bagging通过降低基分类器方差改善了泛化能力,因此bagging的性能依赖于基分类器的稳定性,如果基分类器是不稳定的,bagging有助于减低训练数据的随机扰动导致的误差,但是如果基分类器是稳定的,即对数据变化不敏感,那么bagging方法就得不到性能的提升,甚至会减低,因为新数据集只有63%。
boostig:提升方法是一个迭代的过程,通过改变样本分布,使得分类器聚集在那些很难分的样本上,对那些容易错分的数据加强学习,增加错分数据的权重,这样错分的数据再下一轮的迭代就有更大的作用(对错分数据进行惩罚)。数据的权重有两个作用,一方面我们可以使用这些权值作为抽样分布,进行对数据的抽样,另一方面分类器可以使用权值学习有利于高权重样本的分类器。把一个弱分类器提升为一个强分类器,大家可以参考Adaboost算法。
(2)通过处理数据特征构建差异性分类器
对训练数据抽取不同的输入特征子集分别进行训练,从而构建具有差异性的分类器。一般采用随机子空间,少量余留法(抽取最重要的一些特征),遗传算法等。
(3)对分类器的处理构建差异性分类器
指的就是通过改变一个算法的参数来生成有差异性的同质分类器,比如改变神经网络的网络拓扑结构就可以构建出不同的分类器。
2.对基分类器结果进行整合
1、对于回归预测(数值预测)
(1)简单平均(Simple Average),就是取各个分类器结果的平均值。
(2)加权平均(Weight Average),加权平均。
2、对于分类(类别预测)
(1)简单投票(Major vote):就是每个分类器的权重大小一样,少数服从多数,类别得票数超过一半的作为分类结果
(2)加权投票(Weight Vote):每个分类器权重不一。
(3)概率投票(Soft vote):有的分类器的输出是有概率信息的,因此可用概率投票。
现在我们来说说为什么会集成学习会提高分类器的预测精度?
举个例子:
有5个分类器的正例率分别是{0.7,0.7,0.7,0.9,0.9},采用简单投票方法(必须有三个以上分类正确),那么正确分类的结果有以下几种:
3个分类器正确:0.73*0.1*0.1+3*0.72*2*0.9*0.1+3*0.7*0.32*0.9*0.9
4个分类器正确:0.73*0.9*0.1*2+3*0.72*0.3*0.92
5个分类器正确:0.73*0.92
把这几个相加可得p≈0.933>0.9,同理我们可以证明加权投票的效果会更好。