（Caffe，LeNet）反向传播（六）
本文地址：http://blog.csdn.net/mounty_fsc/article/details/51379395
本部分剖析Caffe中Net::Backward()函数，即反向传播计算过程。从LeNet网络角度出发，且调试网络为训练网络，共9层网络。具体网络层信息见 （Caffe，LeNet）初始化训练网络（三） 第2部分
本部分不介绍反向传播算法的理论原理，以下介绍基于对反向传播算法有一定的了解。
1 入口信息
Net::Backward()函数中调用BackwardFromTo函数，从网络最后一层到网络第一层反向调用每个网络层的Backward。
void Net::BackwardFromTo(int start, int end) {
for (int i = start; i >= end; --i) {
if (layer_need_backward_[i]) {
layers_[i]->Backward(
top_vecs_[i], bottom_need_backward_[i], bottom_vecs_[i]);
if (debug_info_) { BackwardDebugInfo(i); }
}
}
} 2 第九层SoftmaxWithLossLayer
2.1 代码分析
代码实现如下：
void SoftmaxWithLossLayer::Backward_gpu(const vector<<>>(nthreads, top_data, label, bottom_diff,
outer_num_, dim, inner_num_, has_ignore_label_, ignore_label_, counts);
// 代码展开开始,代码有修改
__global__ void SoftmaxLossBackwardGPU(...) {
CUDA_KERNEL_LOOP(index, nthreads) {
const int label_value = static_cast<int>(label[index]);
bottom_diff[index * dim + label_value] -= 1;
counts[index] = 1;
}
}
// 代码展开结束
Dtype valid_count = -1;
// 注意为loss的权值，对该权值（一般为1或者0）归一化（除以64）
// Scale gradient
const Dtype loss_weight = top[0]->cpu_diff()[0];
if (normalize_) {
caffe_scal(prob_.count(), loss_weight / count, bottom_diff);
} else {
caffe_scal(prob_.count(), loss_weight / outer_num_, bottom_diff);
}
} 说明：
1. SoftmaxWithLossLayer是没有学习参数的（见前向计算（五）) ，因此不需要对该层的参数做调整，只需要计算bottom_diff（理解反向传播算法的链式求导，求bottom_diff对上一层的输出求导，是为了进一步计算调整上一层权值）
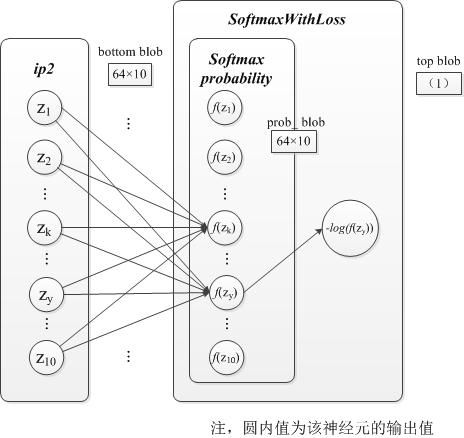
2. 以上代码核心部分在SoftmaxLossBackwardGPU。该函数将bottom_diff（此时为每个类的预测概率）对应的正确类别（label）的概率值-1，其他数据没变。这里使用前几节的符号系统及图片进行解释。
2.2 公式推导
符号系统
设SoftmaxWithLoss层的输入为向量 z ，即bottom_blob_data，也就是上一层的输出。经过Softmax计算后的输出为向量 f(z) ，公式为（省略了标准化常量m） f(zk)=ezk∑niezi 。最后SoftmaxWithLoss层的输出为 loss=∑n−logf(zy) ， y 为样本的标签。见前向计算（五）。
反向推导
把loss展开可得
loss=log∑inezi−zy
所以 dlossdz 结果如下：
∂loss∂zi={f(zy)−1,zi=zyf(zi),zi≠zy图示
3 第八层InnerProduct
3.1 代码分析
template <typename Dtype>
void InnerProductLayer::Backward_gpu(const vector(CblasTrans, CblasNoTrans, N_, K_, M_, (Dtype)1.,
top_diff, bottom_data, (Dtype)1., this->blobs_[0]->mutable_gpu_diff());
}
// 对偏置求偏导top_diff*bias=blobs_diff
if (bias_term_ && this->param_propagate_down_[1]) {
const Dtype* top_diff = top[0]->gpu_diff();
// Gradient with respect to bias
caffe_gpu_gemv(CblasTrans, M_, N_, (Dtype)1., top_diff,
bias_multiplier_.gpu_data(), (Dtype)1.,
this->blobs_[1]->mutable_gpu_diff());
}
//对上一层输出求偏导top_diff*blobs_data=bottom_diff
if (propagate_down[0]) {
const Dtype* top_diff = top[0]->gpu_diff();
// Gradient with respect to bottom data
caffe_gpu_gemm(CblasNoTrans, CblasNoTrans, M_, K_, N_, (Dtype)1.,
top_diff, this->blobs_[0]->gpu_data(), (Dtype)0.,
bottom[0]->mutable_gpu_diff());
}
}
3.2 公式推导
如图，当前层ip2层的输入为 z ，上一层的输入为 u 。
1. 对上一层输出求偏导
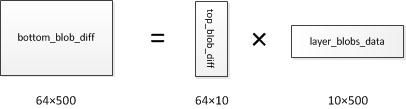
∂loss∂uj 存放在ip2层的bottom_blob_diff（64*500）中，计算公式如下，其中 ∂loss∂zk 存放在top_blob_diff（64*10）中:
∂zk∂uj=∑100jwkjuj∂uj=wkj
∂loss∂uj=∑kn=10∂loss∂zk∂zk∂uj=∑kn=10∂loss∂zkwkj
写成向量的形式为：
∂loss∂uj=∂loss∂zT⋅wj
进一步，写成矩阵的形式，其中 u 为500维， z 为10维， W 为 10×500 ：
∂loss∂uT=∂loss∂zT⋅W
再进一步，考虑到一个batch有64个样本，表达式可以写成如下形式，其中 U 为 64×500 ； Z 为 64×10 ； W 为 10×500 ：
∂loss∂U=∂loss∂Z⋅W
2. 对参数求偏导
∂loss∂wkj=∂loss∂zk∂zk∂wkj=∂loss∂zkuj
写成向量的形式有：
∂loss∂wj=∂loss∂zuj
进一步，可以写成矩阵形式，其中 W 为 10×500 ； z 为10维； u 为500维。
∂loss∂W=∂loss∂zuT
再进一步，考虑到一个batch有64个样本，表达式可以写成如下形式，其中 W 为 10×500 ； Z 为 64×10 ； U 为 64×500 ：
∂loss∂W=∂loss∂ZT⋅U
4 第七层ReLU
4.1 代码分析
cpu代码分析如下，注，该层没有参数，只需对输入求导
void ReLULayer::Backward_cpu(const vector 4.2 公式推导
设输入向量为 bottom_data ，输出向量为 top_data ，ReLU层公式为
top_datai={bottom_dataibottom_datai∗slopebottom_datai>0bottom_datai≤0
所以，loss对输入的偏导为:
∂loss∂bottom_datai=∂loss∂top_datai⋅∂top_datai∂bottom_datai={top_diffitop_diffi∗slopebottom_datai>0bottom_datai≤0
5 第五层Pooling
5.1 代码分析
Maxpooling的cpu代码分析如下，注，该层没有参数，只需对输入求导
void PoolingLayer::Backward_cpu(const vector 5.2 公式推导
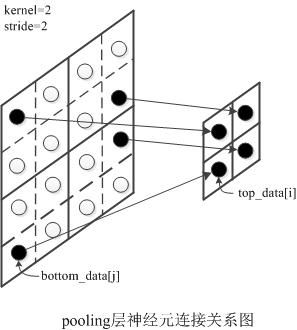
由图可知，maxpooling层是非线性变换，但有输入与输出的关系可线性表达为 bottom_dataj=top_datai （所以需要前向计算时需要记录索引i到索引j的映射max_idx_.
链式求导有：
bottom_diffj=∂loss∂bottom_dataj=∂loss∂top_datai⋅∂top_datai∂bottom_dataj=top_diffi⋅1（注意下标）
6 第四层Convolution
void ConvolutionLayer::Backward_cpu(const vector(CblasNoTrans, CblasTrans, conv_out_channels_ / group_,
kernel_dim_, conv_out_spatial_dim_,
(Dtype)1., top_diff + n * this->top_dim_, bottom_data + n * this->bottom_dim_,
(Dtype)1., weight_diff);
// gradient w.r.t. bottom data, if necessary.
// weight(50*500,Transpose) * top_diff(50*64) = bottom_diff(500*64)
caffe_cpu_gemm(CblasTrans, CblasNoTrans, kernel_dim_,
conv_out_spatial_dim_, conv_out_channels_ ,
(Dtype)1., weight, top_diff + n * this->top_dim_,
(Dtype)0., bottom_diff + n * this->bottom_dim_);
}
}
}
}
说明：
- 第四层的bottom维度 (N,C,H,W)=(64,20,12,12) ，top的维度bottom维度 (N,C,H,W)=(64,50,8,8) ,由于每个样本单独处理，所以只需要关注 (C,H,W) 的维度，分别为 (20,12,12) 和 (50,8,8)
- 根据（Caffe）卷积的实现，该层可以写成矩阵相乘的形式 Weight_data×Bottom_dataT=Top_data
- Weight_data 的维度为 Cout×(C∗K∗K)=50×500
- Bottom_data 的维度为 (H∗W)×(C∗K∗K)=64×500 ， 64 为 8∗8 个卷积核的位置， 500=C∗K∗K=20∗5∗5
- Top_data 的维度为 64×50
- 写成矩阵表示后，从某种角度上与全连接从（也是表示成矩阵相乘）相同，因此，可以借鉴全连接层的推导。